ML-朴素贝叶斯

最新推荐文章于 2025-06-07 22:46:44 发布

原创最新推荐文章于 2025-06-07 22:46:44 发布

· 176 阅读

0 ·

版权

文章标签：

#机器学习

机器学习专栏收录该内容

4 篇文章

订阅专栏

从一个最简单的概率分类器开始，通过给出一些假设（1.各特征之间是独立的；2.每个特征同等重要）来学习朴素贝叶斯分类器。
朴素贝叶斯的核心思想：选择高概率对应的类别。
在这里插入图片描述
贝叶斯准则

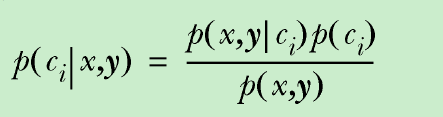
使用这些定义，可以定义贝叶斯分类准则为：
 如果P(c1|x, y) > P(c2|x, y)，那么属于类别c1。
 如果P(c1|x, y) < P(c2|x, y)，那么属于类别c2。

该函数的伪代码：

计算每个类别中的文档数目  #求P(c_0),P(c_1)
对每篇训练文档：
    对每个类别：
        如果词条出现在文档中：增加该词条计数值
        增加所有词条计数值  #求P(w) 
对每个类别：
    对每个词条：
        将该词条的数目除以总词条数目得到条件概率 #求P(w|c_i)

1. 文本预处理：利用文本构建词汇向量
下面代码里给了一段简单的样本做例子，用来简要说明如何处理文本，利用文本构建词汇向量，后面分类器训练函数里也会用到下面的部分代码。

import numpy as np
def loadDataSet(): #导入数据
    #假设数据为最简单的6篇文章，每篇文章大概7~8个词汇左右，如下
    postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0,1,0,1,0,1] #对应上述6篇文章的分类结果，1为侮辱性，0为非侮辱性
    return postingList,classVec 

def createVocabList(dataSet):# 将所有文章中的词汇取并集汇总
    vocabSet = set([])  # 定义一个set(set存储的内容无重复)
    for document in dataSet:# 遍历导入的dataset数据，将所有词汇取并集存储至vocabSet中
        vocabSet = vocabSet | set(document) # | 符号为取并集，即获得所有文章的词汇表
    return list(vocabSet)

#该函数输入参数为词汇表及某篇文章，输出为文档向量，向量每个元素为1或0，分别表示词汇表中的单词在输入文档中是否出现；
def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0]*len(vocabList) #构建一个0向量；
    for word in inputSet: # 遍历词汇表，如果文档中出现了词汇表中单词，则将输出的文档向量中对应值设为1，旨在计算各词汇出现的次数；
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1#因为上一段代码里，给的文章例子里的单词都是不重复的，如果有重复的单词的话，这段代码改写为：returnVec[vocabList.index(word)] += 1更为合适；
        else: print "the word: %s is not in my Vocabulary!" % word
    return returnVec#返回向量化后的某篇文章

2. 训练函数：从词向量计算概率

def trainNB0(trainMatrix, trainCategory):
  numTrainDocs = len(trainMatrix)     # 文档数目，这里是6篇
  numWords = len(trainMatrix[0])      # 唯一词表的长度
  #print(sum(trainCategory))           # 求和，[0, 1, 0, 1, 0, 1]，和是3
  pAbusive = sum(trainCategory)/float(numTrainDocs)   # 6篇里有3篇是侮辱性的，概率为0.5
  p0Num = np.zeros(numWords)              # 全为0的矩阵
  p1Num = np.zeros(numWords)              # 全为0的矩阵
  p0Denom = 0.0
  p1Denom = 0.0 
# 初始化工作
  for i in range(numTrainDocs):       # 对每一篇
      if trainCategory[i] == 1:       # 该篇如果是侮辱性的
          p1Num += trainMatrix[i]     # 因为是二分类所以与0矩阵求和
          p1Denom += sum(trainMatrix[i])  # 矩阵内各元素求和
      else:                           # 非侮辱性
          p0Num += trainMatrix[i]     # 因为是二分类所以与0矩阵求和
          p0Denom += sum(trainMatrix[i])  # 矩阵内各元素求和
  p1Vect = p1Num/p1Denom      # 对矩阵各元素做除法
  p0Vect = p0Num/p0Denom
  return p0Vect, p1Vect, pAbusive

3.测试


if __name__ == '__main__':
  listOPosts, listClasses = loadDataSet()
  myVocabList = createVocabList(listOPosts)

  trainMat = []
  for postinDoc in listOPosts:
    trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
  p0V, p1V, pAb = trainNB0(trainMat, listClasses)
  print(p0V)		# 给定文档类别条件下（非侮辱），词汇表中单词出现概率
  print(p1V)		# 给定文档类别条件下（侮辱），词汇表中单词出现概率
  print(pAb)		# 文档属于侮辱类的概率

要计算多个概率的乘积以获得文档属于某个类别的概率，即计算 p(w0|1) * p(w1|1) * p(w2|1)

如果其中一个概率值为 0，那么最后的乘积也为 0。为降低这种影响，可以将所有词的出现数初始化为 1，并将分母初始化为 2 （取1 或 2 的目的主要是为了保证分子和分母不为0，大家可以根据业务需求进行更改）

另一个遇到的问题是下溢出，这是由于太多很小的数相乘造成的。当计算乘积 p(w0|ci) * p(w1|ci) * p(w2|ci)… p(wn|ci) 时，由于大部分因子都非常小，所以程序会下溢出或者得到不正确的答案。（用 Python 尝试相乘许多很小的数，最后四舍五入后会得到 0）。

一种解决办法是对乘积取自然对数。在代数中有 ln(a * b) = ln(a) + ln(b), 于是通过求对数可以避免下溢出或者浮点数舍入导致的错误。同时，采用自然对数进行处理不会有任何损失。

import numpy as np

def loadDataSet(): #导入数据
    #假设数据为最简单的6篇文章，每篇文章大概7~8个词汇左右，如下
    postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0,1,0,1,0,1] #对应上述6篇文章的分类结果，1为侮辱性，0为非侮辱性
    return postingList,classVec 

def createVocabList(dataSet):# 将所有文章中的词汇取并集汇总
    vocabSet = set([])  # 定义一个set(set存储的内容无重复)
    for document in dataSet:# 遍历导入的dataset数据，将所有词汇取并集存储至vocabSet中
        vocabSet = vocabSet | set(document) # | 符号为取并集，即获得所有文章的词汇表(数学上，按位或操作与集合求并操作使用相同符号)
    return list(vocabSet)

#该函数输入参数为词汇表及某篇文章，输出为文档向量，向量每个元素为1或0，分别表示词汇表中的单词在输入文档中是否出现；
def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0]*len(vocabList) #构建一个0向量；
    for word in inputSet: # 遍历词汇表，如果文档中出现了词汇表中单词，则将输出的文档向量中对应值设为1，旨在计算各词汇出现的次数；
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1#因为上一段代码里，给的文章例子里的单词都是不重复的，如果有重复的单词的话，这段代码改写为：returnVec[vocabList.index(word)] += 1更为合适；
        else: print( "the word: %s is not in my Vocabulary!" % word)
    return returnVec#返回向量化后的某篇文章

def trainNB0(trainMatrix, trainCategory):
  numTrainDocs = len(trainMatrix)     # 文档数目，这里是6篇
  numWords = len(trainMatrix[0])      # 唯一词表的长度
  #print(sum(trainCategory))           # 求和，[0, 1, 0, 1, 0, 1]，和是3
  pAbusive = sum(trainCategory)/float(numTrainDocs)   # 6篇里有3篇是侮辱性的，概率为0.5
  p0Num = np.ones(numWords)              # 全为0的矩阵
  p1Num = np.ones(numWords)              # 全为0的矩阵
  p0Denom = 2.0
  p1Denom = 2.0 
  p1Vect = np.log(p1Num/p1Denom)      # 对矩阵各元素做除法
  p0Vect = np.log(p0Num/p0Denom)
# 初始化工作
  for i in range(numTrainDocs):       # 对每一篇
      if trainCategory[i] == 1:       # 该篇如果是侮辱性的
          p1Num += trainMatrix[i]     # 因为是二分类所以与0矩阵求和
          p1Denom += sum(trainMatrix[i])  # 矩阵内各元素求和
      else:                           # 非侮辱性
          p0Num += trainMatrix[i]     # 因为是二分类所以与0矩阵求和
          p0Denom += sum(trainMatrix[i])  # 矩阵内各元素求和
  p1Vect = p1Num/p1Denom      # 对矩阵各元素做除法
  p0Vect = p0Num/p0Denom
  
  return p0Vect, p1Vect, pAbusive
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    print(sum(vec2Classify * p1Vec))
    p1 = sum(vec2Classify * p1Vec) + np.log(pClass1)    
    # log()是因为我们之前得出的概率取了对数，所以这里变成了相加
    # 由于是取对数，所以乘积变为直接求和即可，注意这里list和list是无法相乘，vec2Classify需要为array格式
    p0 = sum(vec2Classify * p0Vec) + np.log(1.0 - pClass1)
    if p1 > p0:
        return 1
    else:
        return 0


if __name__ == '__main__':
    listOPosts, listClasses = loadDataSet()
    myVocabList = createVocabList(listOPosts)
    trainMat = []
    for postinDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
    p0V, p1V, pAb = trainNB0(np.array(trainMat), np.array(listClasses))
    testEntry = ['love', 'my', 'dalmation']
    thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry))
    print(thisDoc)
    print(testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb))
    testEntry = ['stupid', 'garbage']
    thisDoc1 = np.array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry, 'classified as: ', classifyNB(thisDoc1, p0V, p1V, pAb))

运行结果：

[0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0]
0.14285714285714285
['love', 'my', 'dalmation'] classified as:  0
0.2857142857142857
['stupid', 'garbage'] classified as:  1

心得体会：
numpy模块下的array与mat函数的区别：
1.生成矩阵。
mat可以用以下两种方式生成矩阵，其效果完全相同。
array生成矩阵，则只有一种方式。

import numpy as np
a = np.mat([[1,2],[3,4]])
b = np.mat('1 2;3 4')
c=np.array([[1,2],[3,4]])#只有这一种
print(a)
print(b)
print(c)

结果：

[[1 2]
 [3 4]]
[[1 2]
 [3 4]]
[[1 2]
 [3 4]]

矩阵的乘法：
mat与array生成的矩阵均可以调用numpy.multiply()函数来实现对应位置元素相乘；mat与array形成的矩阵均可以调用dot（）函数来实现矩阵的乘法（数学中的矩阵乘法）

import numpy as np
a = np.mat([[1,2],[3,4]])
b = np.mat('2 3;4 5')
print(np.multiply(a,b))
print(np.dot(a,b))

结果：

[[ 2  6]
 [12 20]]
[[10 13]
 [22 29]]

使用星号时两者实现的操作不同：对array函数生成的矩阵来说，星号实现的对应位置元素的乘积；而对于mat函数生成的矩阵来说，星号*实现的是矩阵的乘积

import numpy as np
a = np.mat([[1,2],[3,4]])
b = np.mat('2 3;4 5')
c = np.array([[1,2],[3,4]])
d = np.array([[2,3],[4,5]])
print('a*b=',a*b)
print('c*d=',c*d)

结果：

a*b= [[10 13]
 [22 29]]
c*d= [[ 2  6]
 [12 20]]

文档词袋模型：
前面实现的词汇表仅仅可以表示词汇表中的单词是否在待测试文档中出现，而不能表示出现的频率，i因此对前面的setOfWords2Vec函数进行相应的修改，使其能表示词频。

def bagOfWords2VecMN(vocabList, inputSet):
    returnVec = [0]*len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] += 1
    return returnVec