KMP算法

KMP算法
KMP算法又称匹配模式算法，能够在线性时间内判定字符串A是否为字符串B的子字符串，并求出字符串A在字符串B中各次出现的次数。简单来说就是我们平时常说的关键字搜索。模式串就是关键字，如果它在一个主串中出现，就返回它的具体位置。
其实这类问题用Hash也能求，知道A的区间长度M，枚举B的每个位置i，检查字符串A的Hash值与B的子串A[i-M+1,i]的Hash值是否相同
KMB算法实现：

1. 对字符串的自我匹配，求出一个数组next，其中next其中next[i]，表示“A中以i结尾的非前缀子串”与“A的前缀子串”能够匹配的最长长度，即：
   next[i]=max{j},其中j<i并且A[i-j+1,i]=A[1,i]
2. 对字符串A与B进行匹配，求出一个数组f，其中f[i]表示“B中以i结尾的子子串”与“A的前缀”能够匹配的最长长度，即;
   f[i]=max{j}，其中j<i并且B[i-j+1,i]=A[1,j]
   其实上面的实现我一看就蒙了，自身与自身匹配是什么鬼，最后查了一下才发现这里省去了一些步骤，我觉得有必要说一下：
   
   
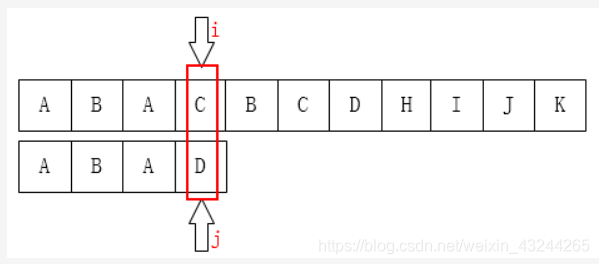
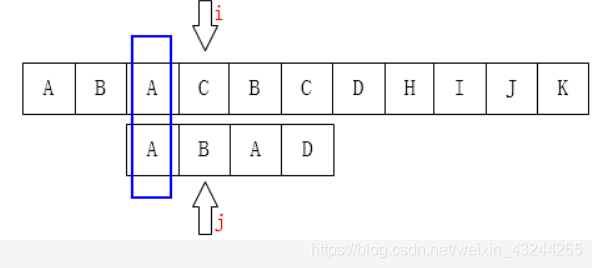
   就上面的情况我们一般是将A的起点移动到下一位，但这里因为A B的第二位匹配并且A的第一位与第二位不同，所以很明显的这一步是多余的，所以我们便想到移动到下一个”A”的位置，但如果i不动的情况下要想i后面的匹配i前面都匹配是前题，所以不是要移动到下一个“A”而是要移动到i前全部匹配的一个，即未移动时的j的向前数k项要与B的头k项匹配，这就是自我匹配的来源。.