李宏毅ML-03-Gradient Decent 2

梯度下降的tips

Outline

• Adagard
• Stochastic Gradient Descent
• Feature Scaling
• Math theory of gradient descent

1 Adagrad

常用的思想就是使得learning rate随着参数的update慢慢变小。距离极值较远的时候使用较大的的learning rate，距离极值较近的时候使用较小的learning rate。

1.1 Adagrad原理

Adagrad 给每个参数赋予不同的随时间变化的学习率。具体更新式子如下：
$$w_{t+1}=w_t-\frac{{\eta }_t}{{\sigma }_t}\frac{\partial L}{\partial w}$$
其中:
$${\eta }_t=\frac{\eta }{\sqrt{t+1}}$$
设偏微分使用 $g=\frac{\partial L}{\partial w}$来表示
$${\sigma }_t=\sqrt{\frac{g_0^2+g_1^2+...+g_t^2}{t+1}}$$
我们观察到两个式子的分母都是$\sqrt{t+1}$, 所以最后的更新式子可以是：
$$w_{t+1}=w_t-\frac{\eta }{\sqrt{g_0^2+g_1^2+...+g_t^2}}{g}_t$$

---

Adagrad是可调节学习率中比较简单的一种，那么为什么这种方法的道理是什么呢？从数学上如何解释Adagrad？

1.2 Adagrad解释

梯度下降的最佳step每次是多少？我们以一个二次函数为例：
$$y=a{x}^2+bx+c$$

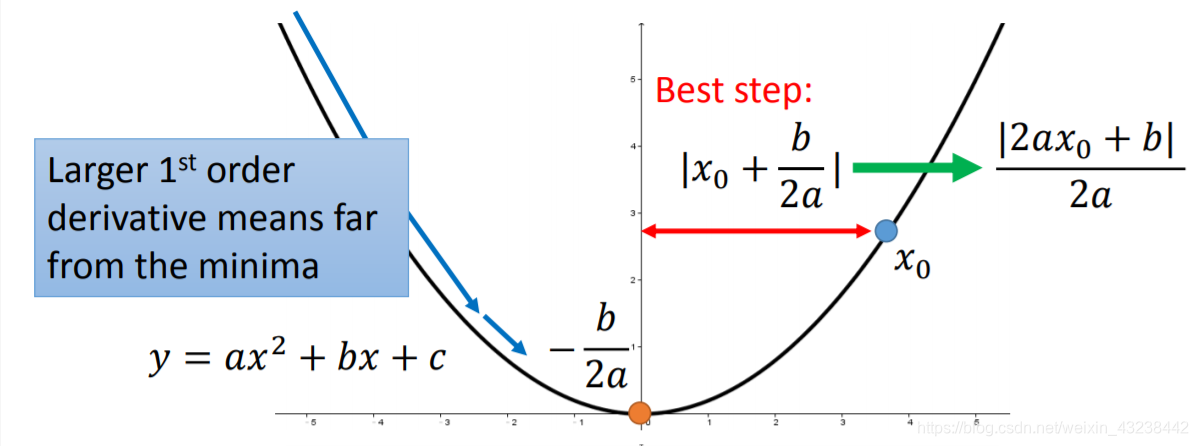
在任意$x_0$距离最低点的水平距离就是：
$$\frac{\left|\begin{array}{c}2a{x}_0+b\end{array}\right|}{2a}$$
很明显分子是函数的一次导数，分母是一个常数（其实就是二次导数）；从这个式子看距离最低点越远导数越大，一次移动就越远；离最低点越近导数越小，移动的距离越小。这反映了梯度下降的合理性。
然而这只在一元函数中成立，多元函数必须将分母看作二次倒数/二次偏导数这个分式才能反映$x_0$到最低点的距离。我们只需要比较这个式子就可以知道$x$距离最低点的远近关系，越远越大，跃进越近越小。
In conclusion: 任一点$x_0$到最低点的距离是函数在这一点的一次导数和二次导数的比值。

---

这就说明梯度下降的幅度要和一次导数成正比，二次倒数成反比。我们回到Adagrad的式子$$w_{t+1}=w_t-\frac{\eta }{\sqrt{g_0^2+g_1^2+...+g_t^2}}{g}_t$$
其实是符合这个关系的。我们用之前导数的root mean square来反映二次导数的大小，为什么？
如下图所示，当我们在某一点周围取地足够多的一次导数，就能大概知道在这一点的二次导数是个什么样子：途中黑点为sampling的点。

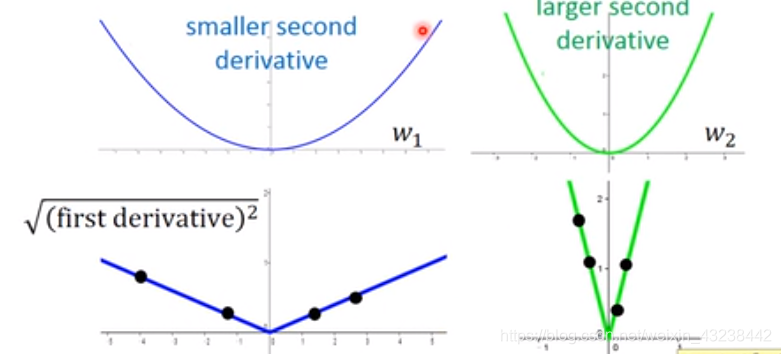
这就是Adagrad最核心的思想，总结为两点：

• 任一点距离最低点的距离可以用这一点导数和二次导数比值 or 偏导数和二次偏导数比值来反映；这与我们update参数的幅度有关；
• 任一点的二次导数 or 二次偏导数可以用附近点的一次导数 or 偏导数的 $rootmeansquare$来反映；

2 Stochastic Gradient Descent随机梯度下降

基本思想与一般梯度下降相同，但是一般梯度下降要看完所有data之后才会update一次参数，随机梯度下降每看一组data就会update一次参数。这样使得我们的模型会比较快的收敛。

3 Feature Scaling

如果不同的feature数量级差别很大会对参数的更新产生麻烦，大数量级对应参数改变一点就对函数值有明显影响，而其他的feature对应参数改变很多可能影响微不足道。这时候特这缩放来解决这个问题。
对于每一个feature（也就是每一dimension）都进行特征缩放：

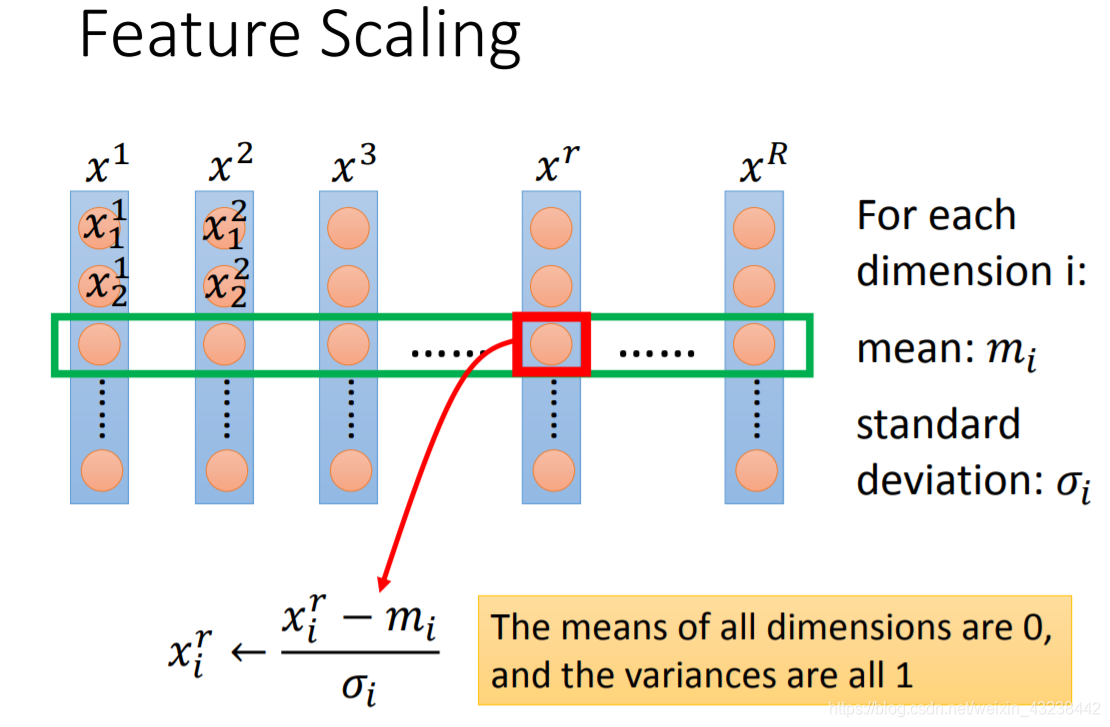
具体公式如上图所示，这时所有唯独的数据都会变成均值为0，方差为1的数据；处在一个较为集中的范围内。

数学原理

首先，是不是每次更新参数都会得到$$L({\theta }_0)>L({\theta }_1)>L({\theta }_2)>...>L({\theta }_n)$$
答案很明显是否定的。从第一篇文章可以看出，如果学习率过大可能导致L的值逐渐增大。

Multiple Taylor Series多元泰勒级数

微积分中Taylor series可以简化函数，这里我们就应用一下，用多元Tayor Polynomial来简化我们的Loss Function。首先给出二元Taylor Series（更多元以此类推）：
$$h(x,y)=h(x_0,y_0)+\frac{\partial h(x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial h(x_0,y_0)}{\partial y}(y-y_0)+moretermsabout(x-x_0)and(y-y_0)$$
这里我们只取前三项，当$(x,y)$很接近$(x_0,y_0)$，后面的项太小了可以忽略不计。现在给定一个点$(x_0,y_0)$ Taylor 公式就可以告诉我们在这一点周围和小的范围之内的值都可以使用上面的公式来求解。

现在回到Loss Function（假设给定点（a,b)）：
$$L(\theta )=s+u({\theta }_1-a)+v({\theta }_2-b)$$
其中
$$s=L(a,b);u=\frac{\partial L(a,b)}{\partial {\theta }_1};v=\frac{\partial L(a,b)}{\partial {\theta }_2}$$