本文详细介绍了分支界限法，包括其定义、基本思想、与回溯法对比、算法设计思想及提高效率的方法。还给出多个算法实例，如单源最短路径、0 - 1背包、装载、旅行商和布线问题，阐述各问题的描述、分析及解决方法。
对，后面很多地方都打成了分支界限法，懒得改了..gg
一.关于分支界限法的一些
目录
东西
1.什么是分支界限法
所谓“分支”就是采用广度优先的策略，依次搜索活结点的所有分支，也就是所有相邻结点。
为了有效的选择下一扩展结点，以加速搜索的进程，在每一活结点处，计算一个函数值（限界函数），并根据这些已计算出的函数值，从当前活结点表中选择一个最有利的结点作为扩展结点，使搜索朝着解空间树上有最优解的分支推进，以便尽快地找出一个最优解。
2.基本思想
分支限界法常以广度优先或以最小耗费（最大效益）优先的方式搜索问题的解空间树。
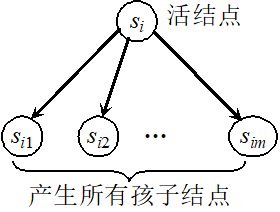
在分支限界法中，每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点。在这些儿子结点中，导致不可行解或导致非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中。
此后，从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。
3.回溯法vs分支界限法
| 方法 | 对解空间树的搜索方式 | 存储结点的常用数据结构 | 结点存储特性 | 主要应用 |
| 回溯法 | 深度优先搜索 | 搜索过程中动态产生问题的解空间 | 活结点的所有可行子结点被遍历后才被从栈中弹出 | 找出满足约束条件的所有解 |
| 分支限界法 | 广度优先或最小耗费优先搜索 | 队列、优先队列 | 每个结点只有一次成为活结点的机会 | 找出满足约束条件的一个解或特定意义下的最优解 |
4.算法设计思想
1. 设计合适的限界函数
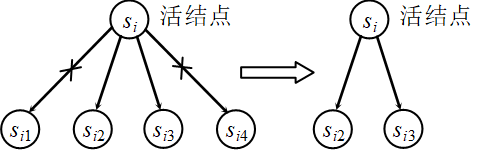
在搜索解空间树时，每个活结点可能有很多孩子结点，其中有些孩子结点搜索下去是不可能产生问题解或最优解的。
可以设计好的限界函数在扩展时删除这些不必要的孩子结点，从而提高搜索效率。
如图所示，假设活结点si有4个孩子结点，而满足限界函数的孩子结点只有2个，可以删除这2个不满足限界函数的孩子结点，使得从si出发的搜索效率提高一倍。
2. 组织活结点表
在分支限界法中，每一个活结点只有一次机会成为扩展结点。
–活结点一旦成为扩展结点，就一次性产生其所有儿子结点。
–在这些儿子结点中，导致不可行解或导致非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中。
–从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。
这个过程一直持续到找到所需的解或活结点表为空时为止。
从活结点表中选择下一个活结点作为新的扩展结点，不同的活结点表对应不同的分支搜索方式。常见的有队列式分支限界法和优先队列式分支限界法两种。
①队列式分支限界法
队列式分支限界法将活结点表组织成一个队列，并按照队列先进先出（FIFO）原则选取下一个结点为扩展结点。
①将根结点加入活结点队列。
②从活结点队中取出队头结点，作为当前扩展结点。
③对当前扩展结点，先从左到右地产生它的所有孩子结点，用约束条件检查，把所有满足约束条件的孩子结点加入活结点队列。
④重复步骤②和③，直到找到一个解或活结点队列为空为止。
②优先队列式分支限界法
优先队列式分支限界法的主要特点是将活结点表组组成一个优先队列，并选取优先级最高的活结点成为当前扩展结点。
①计算起始结点（根结点）的优先级并加入优先队列（与特定问题相关的信息的函数值决定优先级）。
②从优先队列中取出优先级最高的结点作为当前扩展结点，使搜索朝着解空间树上可能有最优解的分支推进，以便尽快地找出一个最优解。
③对当前扩展结点，先从左到右地产生它的所有孩子结点，然后用约束条件检查，对所有满足约束条件的孩子结点计算优先级并加入优先队列。
④重复步骤②和③，直到找到一个解或优先队列为空为止。
3. 确定最优解的解向量
分支限界法在搜索解空间树时，结点的处理是跳跃式的，回溯也不是单纯地沿着双亲结点一层一层地向上回溯，因此当搜索到某个叶子结点且该结点对应一个可行解时，如何得到对应的解向量呢？
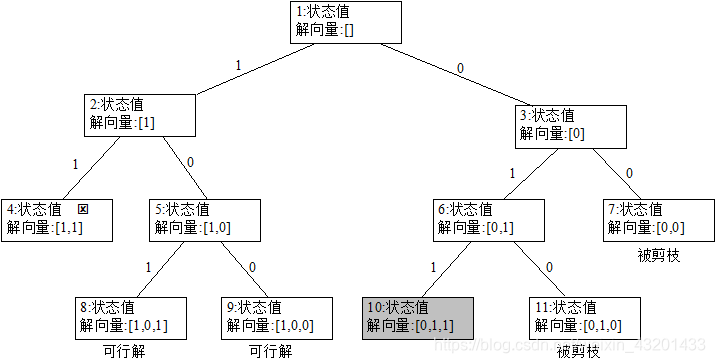
① 对每个扩展结点保存从根结点到该结点的路径
如图，结点编号为搜索顺序，每个结点带有一个可能的解向量，带阴影的结点为最优解结点，对应的最优解向量为[0,1,1]。这种做法比较浪费空间，但实现起来简单。
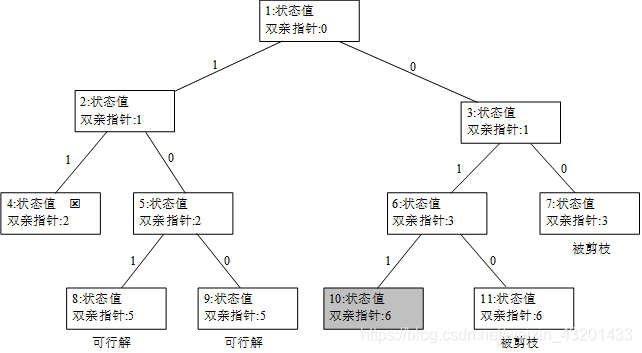
② 在搜索过程中构建搜索经过的树结构
如图，结点编号为搜索顺序，每个结点带有一个双亲结点指针，带阴影的结点为最优解结点，当找到最优解时，通过双亲指针找到对应的最优解向量为[0,1,1]。这种做法需保存搜索经过的树结构，增加了指向双亲结点的指针。
5.提高分支限界法效率
实现分支限界算法时，首先确定目标值的上下界，边搜索边减掉搜索树的某些分支，提高搜索效率。
在搜索时，绝大部分需要用到剪枝。“剪枝”是搜索算法中优化程序的一种基本方法，需要通过设计出合理的判断方法，以决定某一分支的取舍。
若我们把搜索的过程看成是对一棵树的遍历，那么剪枝就是将树中的一些“死结点”，不能到达最优解的枝条“剪”掉，以减少搜索的时间。
也需要考虑一些问题，比如..................
1）对于最大值（或者最小值）问题，需要考虑如何估算上界（或下界）值。
2）怎样从活结点表中选择一个节点作为扩展结点。
3）怎样展开一棵搜索树，是宽度优先搜索，还是宽度优先结合深度优先进行混合搜索。
二.算法实例
1.单源最短路径问题（了解思想，会画出树）
问题描述
给定带权有向图G＝(V，E)，其中每条边的权是非负实数。
给定V中的一个顶点，称为源。
要计算从源到所有其它各顶点的最短路长度，这里路的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。
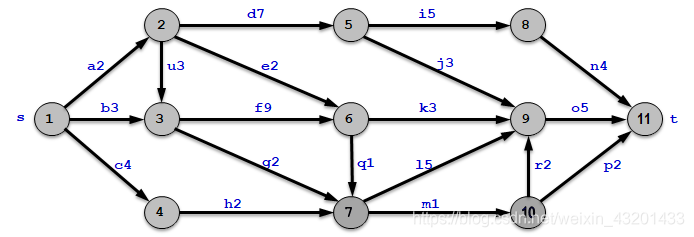
输入：第一行是顶点个数n，第二行是边数edge；接下来edge行是边的描述：from，to，d，表示从顶点from到顶点to的边权是d。
后面是若干查询，从顶点s到顶点t。
输出：给出所有查询，从顶点s到顶点t的最短距离。
如果从顶点s不可达到顶点t，则输出“No path!”。
| 输入样例 | 输出样例 |
| 6 8 1 3 10 1 5 30 1 6 100 2 3 5 3 4 50 4 6 10 5 4 20 5 6 60 1 2 1 3 1 4 1 5 1 6 3 4 3 6 4 6 | No path! 10 50 30 60 50 60 10 |
问题分析
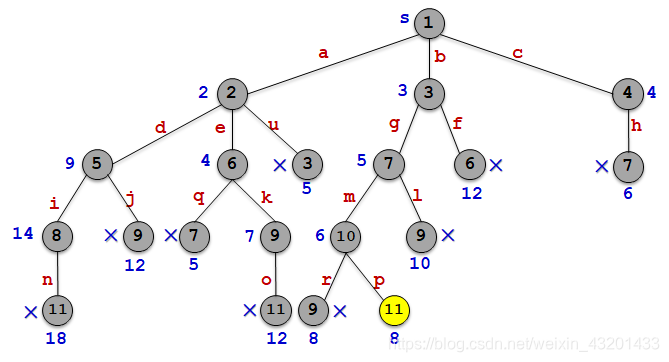
解单源最短路径问题的优先队列式分支限界法，其优先级是结点所对应的当前路长。
①算法从图G的源顶点s和空优先队列开始。结点s被扩展后，它的儿子结点a，b，c被依次插入优先队列中。
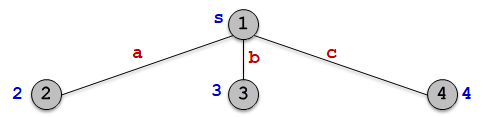
| 结点 | 2 | 3 | 4 |
|
|
|
| 路径长度 | 2 | 3 | 4 |
|
|
|
②算法从优先队列中取出具有最小当前路长的结点作为当前扩展结点，并依次检查与当前扩展结点相邻的所有顶点。
③如果从当前扩展结点i到顶点j有边可达，且从源出发，途经顶点i再到顶点j相应的路径的长度小于当前最优路径长度，则将该顶点作为活结点插入到活结点优先队列中。
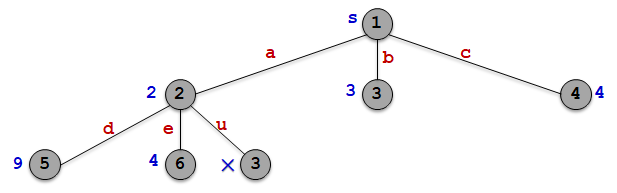
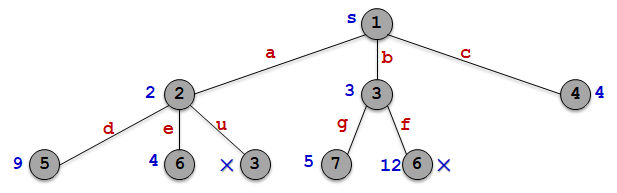
| 结点 | 4 | 6 | 7 | 5 |
|
|
| 路径长度 | 4 | 4 | 5 | 9 |
|
|
这个结点的扩展过程一直继续到活结点优先队列为空。
#define inf 10000000
#define NUM 100
int n;//顶点数
int edge;//边数
int c[NUM][NUM];//邻接矩阵
int prev[NUM];//前驱顶点数组
int dist[NUM];//从源顶点到各个顶点最短距离数组
struct min
{
//排序算法，升序
friend bool operator < (const MinHeapNode& a,const MinHeapNode& b)
{ if(a.length > b.length) return true;
else return false;
}
int i; //结点编号
int length; //结点路径的长度
};
void shortest(int v)
{
priority_queue <MinHeapNode, vector<MinHeapNode>, less<MinHeapNode> > H;
min e;
e.i = v;
e.length = 0;
dist[v] = 0;
while(true)
{
for(int j = 1;j <= n;j++)//扩展所有子结点
{
//剪枝
if(c[e.i][j] < inf && (e.length + c[e.i][j] < dist[j]))
{
dist[j] = e.length + c[e.i][j];
prev[j] = e.i;
min n;
n.i = j;
n.length = dist[j];
H.push(N);
}
if(H.empty())
break;
else
{
e = H.top();
H.pop();
}
}
}
}2.0-1背包问题（思想）
问题描述
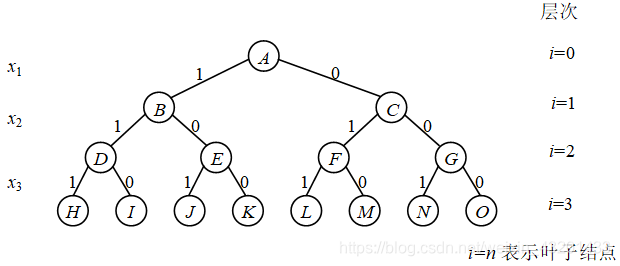
假设一个0/1背包问题是，n=3，重量为w=（16,15,15），价值为v=（45,25,25），背包限重为W=30，解向量为x=（x1,x2,x3），其解空间树如图所示。本节通过队列式和优先队列式两种分支限界法求解该问题。
问题分析
法1：采用队列式分支限界法
首先不考虑限界问题，用FIFO表示队列，初始时，FIFO=[ ]，其求解过程如下：
①根结点A(0,0)进队（括号内两个数分别表示此状态下装入背包的重量和价值，初始时均为0），FIFO=[A]。
②出队A，其孩子结点B(16,45)、C(0,0)进队，FIFO=[B,C]。
③出队B，其孩子D(31,70)变为死结点、只有孩子E(16,45)进队，FIFO=[C,E]。
④出队C，其孩子F(15,25)和G(0,0)进队， FIFO=[E,F,G]。
⑤出队E，其孩子J(31,70)变为死结点（超重），孩子K(16,45)是叶子结点，总重量<W，为一个可行解，总价值为45，对应的解向量为（1,0,0），FIFO=[F,G]。
⑥出队F，其孩子L(30,50)为叶子结点，构成一个可行解，总价值为50，解向量=（0,1,1）；其孩子M(15,25)为叶子结点，构成一个可行解，总价值为25，解向量=（0,1,0）。FIFO=[G]。
⑦出队G，其孩子N(15,25)为叶子结点，构成一个可行解，总价值为25，解向量=（0,0,1）；其孩子O(0,0)为叶子结点，构成一个可行解，总价值为0，解向量=（0,0,0）。FIFO=[]。
⑧因为FIFO=[ ]，算法结束。
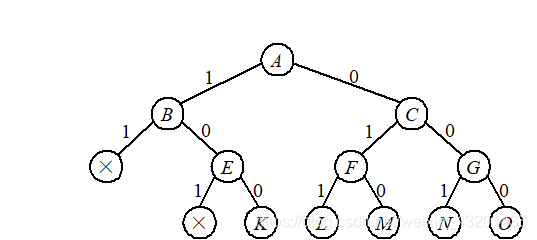即最优解向量为（0，1，1），总价值为50
现在设计限界函数，为了简便，设根结点为第0层，然后各层依次递增，显然i=n时表示是叶子结点层。
求装入背包的最大价值，属求最大值问题，采用上界。
因为要尽可能地装入最有价值的物品，为此将物品按单位重量的价值递减排序，也就是说在重量不超重的条件下先选取单位价值高的物品。对于第i层的某个结点e，用e.w表示搜索到结点e时已装入的总重量，用e.v表示已装入的总价值，如果所有剩余的物品都能装入背包，那么价值的上界e.ub显然是e.v+?=?+1??[?]∑_(j=i+1)^n▒〖v[j]〗；如果所有剩余的物品不能全部装入背包，那么价值的上界e.ub应是e.v+?=?+1??[?] ∑_(j=i+1)^n▒〖v[j]〗 +(物品k+1装入的部分重量)×物品k+1的单位价值。这样每个结点实际装入背包的价值一定小于等于该上界。
例如在上图中，根结点A的层次i=0，w=0，v=0，其ub=0+45+(30-16)×25/15=68（为了简单，均采用取整运算）；结点F中w=15，v=25，i=2，其ub=25+(30-15) ×25/15=50。
问题解决
求解最优解的过程是，先将求出上界的根结点进队。
在队不空时循环：出队一个结点e，检查其左孩子结点并求出其上界，若满足约束条件（e.w+w[e.i+1]≤W），将其进队，否则该左孩子结点变成死结点；
再检查其右孩子结点并求出其上界，若它是可行的（即其上界大于当前已找到可行解的最大总价值maxv，否则沿该结点搜索下去不可能找到一个更优的解），则将该右孩子结点进队，否则该右孩子结点被剪枝。
这一过程循环到队列为空。算法最后输出最优解向量和最大总价值。
①求结点e的上界ub
//求结点e的上界e.ub
void bound(int w[], int v[], int w, int n, Elemtype &e)
{
int i = e.i + 1;
int sumw = e.w;
double sumv = e.v;
while((sumw + w[i] <= w) && i <= n)
{
sumw += w[i];
sumv +=v[i];
i++;
}
if(i <= n)//余下物品只能部分装入
e.ub = sumw + (w - sumw) * v[i] / w[i];
else//余下物品可全部装入
e.ub = sumv;
} ②求最优解
void knap(int w[],int v[],int W,int n)
//求0/1背包的最优解
{ int j;
QueueType q; //建立一个队列
initQueue(q); //队列初始化
ElemType e,e1,e2; //定义3个结点
e.i=0; //根结点置初值，其层次计为0
e.w=0;
e.v=0;
e.no=count++;
for (j=1;j<=n;j++)
e.x[j]=0;
bound(w,v,W,n,e); //求根结点的上界
enQueue(q,e,n); //根结点进队
while (!emptyQueue(q)) //队不空循环
{
deQueue(q,e); //出队结点e
if (e.w+w[e.i+1]<=W) //检查左孩子结点
{
e1.no=count++;
e1.i=e.i+1; //建立左孩子结点
e1.w=e.w+w[e1.i];
e1.v=e.v+v[e1.i];
copyx(e.x,e1.x,e.i);
e1.x[e1.i]=1;
bound(w,v,W,n,e1); //求左孩子结点的上界
enQueue(q,e1,n);
}
e2.no=count++;
e2.i=e.i+1; //建立右孩子结点
e2.w=e.w; e2.v=e.v;
copyx(e.x,e2.x,e.i);
e2.x[e2.i]=0;
bound(w,v,W,n,e2); //求右孩子结点的上界
if (e2.ub>maxv) //若右孩子结点可行,则进队,否则被剪枝
enQueue(q,e2,n);
}
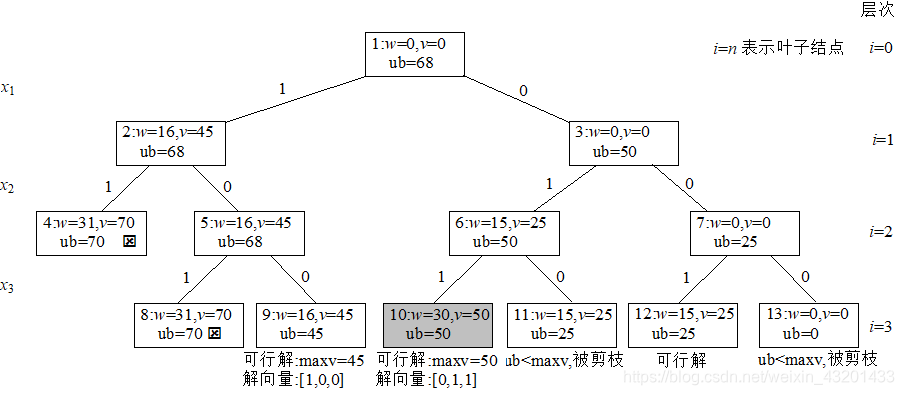
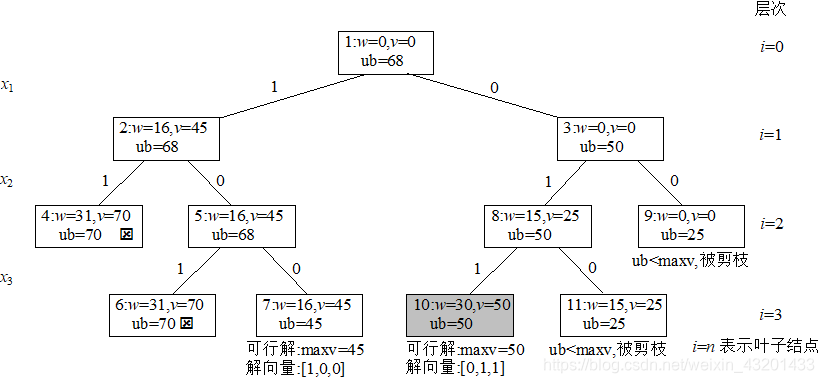
}采用限界函数剪枝的队列式分支限界法求解上述0/1背包问题的搜索空间如图所示，图中带有ý的结点表示死结点，带阴影的结点是最优解结点，结点的编号为搜索顺序，从中看到由于采用队列，结点的扩展是一层一层顺序展开的，类似于广度优先搜索。
法2：采用优先队列式分支限界法
采用优先队列式分支限界法求解必须设计限界函数，因为优先级是以限界函数值为基础的。限界函数的设计方法同“采用队列式分支限界法求解”。这里用大根堆表示活结点表，取优先级为活结点所获得的价值。其求解过程与“采用队列式分支限界法求解”相似，只是将队列操作改为优先队列的操作。
采用限界函数剪枝的优先队列式分枝限界法求解上述0/1背包问题的搜索空间如图所示，图中带有ý的结点表示死结点，带阴影的结点是最优解结点，结点的编号为搜索顺序。
void knap(int w[],int v[],int W,int n)
//求0/1背包问题的最优解
{ int j;
int ew=0,ev=0;
HeapType heap; //建立一个堆
initHeap(heap); //堆初始化
ElemType e,e1,e2;
e.i=0; //i为搜索空间的层次,从第0层开始
e.w=0; e.v=0;
e.no=count++;
for (j=1;j<=n;j++)
e.x[j]=0;
bound(w,v,W,n,e); //求根结点的上界
insertHeap(heap,e,n); //根结点进队
while (!emptyHeap(heap)) //队不空循环
{
delHeap(heap,e); //出队结点e
if (e.w+w[e.i+1]<=W) //检查左孩子结点
{
e1.no=count++;
e1.i=e.i+1; //建立左孩子结点
e1.w=e.w+w[e1.i]; e1.v=e.v+v[e1.i];
copyx(e.x,e1.x,e.i); e1.x[e1.i]=1;
bound(w,v,W,n,e1); //求左孩子结点的上界
insertHeap(heap,e1,n);
}
e2.no=count++;
e2.i=e.i+1; //建立右孩子结点
e2.w=e.w; e2.v=e.v;
copyx(e.x,e2.x,e.i); e2.x[e2.i]=0;
bound(w,v,W,n,e2); //求右孩子结点的上界
if (e2.ub>maxv) //若右结点可行,则右结点进队
insertHeap(heap,e2,n);
}
}从中看到由于采用优先队列，结点的扩展不再是一层一层顺序展开的，而是按限界函数值的大小选取的。该求解过程实际搜索的结点个数为11，比队列式分枝限界法求解最好，当物品数较多时，这种效率的提高会更为明显。
算法分析：无论采用队列式分枝限界法还是优先队列式分枝限界法求解0/1背包问题，最坏情况下要搜索整个解空间树，所以最坏时间和空间复杂度均为O(2^n)，其中n为物品个数。
3.装载问题
①基本问题
问题描述
给定n个集装箱要装上一艘载重量为c的轮船，其中集装箱i的重量为wi。集装箱装载问题要求确定在不超过轮船载重量的前提下，将尽可能多的集装箱装上轮船。
由于集装箱问题是从n个集装箱里选择一部分集装箱，假设解向量为X(x1, x2, …, xn)，其中xi∈{0, 1}， xi =1表示集装箱i装上轮船， xi =0表示集装箱i不装上轮船。
输入：每组测试数据：第1行有2个整数c和n。C是轮船的载重量（0＜c＜30000），n是集装箱的个数（n≤20）。第2行有n个整数w1, w2, …, wn，分别表示n个集装箱的重量。
输出：对每个测试例，输出两行：第1行是装载到轮船的最大载重量，第2行是集装箱的编号。
其实这个问题需要满足的条件抽象出来就是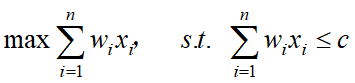
输入样例
80 4
18 7 25 36
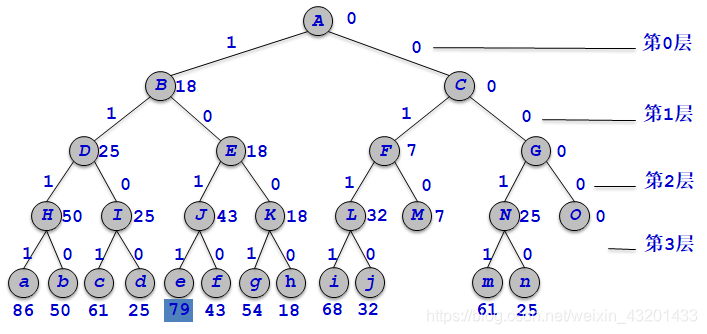
输出样例 79
问题分析
队列式分支限界法
定义一个先进先出（FIFO）队列Q，初始化队列时，在尾部增加一个－1标记。
这是一个分层的标志，当一层结束时，在队列尾部增加一个－1标志。
定义扩展结点相应的载重量为Ew，剩余集装箱的重量为r，当前最优载重量为bestw，轮船的载重量为c＝80。
| Q.front()←→Q.back() | ||||||
| -1 |
|
|
|
|
|
|
算法从子集树的第0层开始展开。
第0层即集装箱0的重量w[0]＝18，是否装入轮船的两种状态。
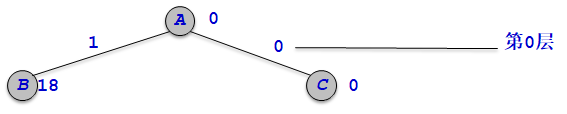
在第0层，Ew＝0，bestw＝0，r＝w[1]＋w[2]＋w[3]＝68，Ew＋w[0]＜c，Ew＋r＞bestw，结点B和C依次进入队列。
| Q.front()←→Q.back() | ||||||
| -1 | 18 | 0 |
|
|
|
|
从队列中取出活结点—1，由于队列不为空，表示当前层结束，新的一层开始，在队列尾部增加一个－1标记。
| Q.front()←→Q.back() | ||||||
| -1 | 18 | 0 |
|
|
|
|
| Q.front()←→Q.back() | ||||||
| 18 | 0 | -1 |
|
|
|
|
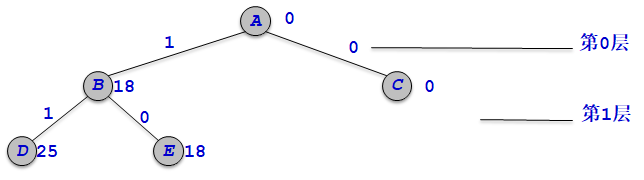
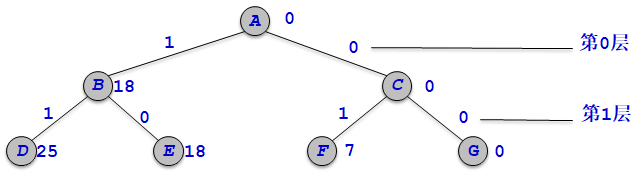
从队列中取出活结点Ew＝18，即结点B。
–第1层即集装箱1的重量w[1]＝7，bestw＝18，r＝w[2]＋w[3]＝61，Ew＋w[1]＝25＜c，Ew＋r＝79＞bestw，结点D和E依次进入队列。
| Q.front()←→Q.back() | ||||||
| 18 | 0 | -1 |
|
|
|
|
| Q.front()←→Q.back() | ||||||
| 0 | -1 | 25 | 18 |
|
|
|
•从队列中取出活结点Ew＝0，即结点C。
–bestw＝25，r＝w[2]＋w[3]＝61，由于Ew＋w[1]＝7＜c，Ew＋r＝61＞bestw，结点F和G依次进入队列。
| Q.front()←→Q.back() | ||||||
| 0 | -1 | 25 | 18 |
|
|
|
| Q.front()←→Q.back() | ||||||
| -1 | 25 | 18 | 7 | 0 |
|
|
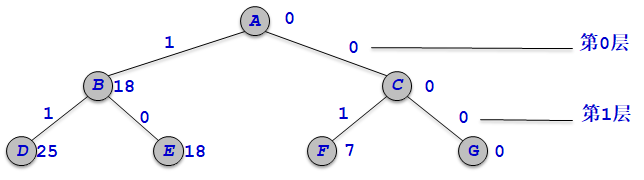
从队列中取出活结点—1，由于队列不为空，表示当前层结束，新的一层开始，在队列尾部增加一个－1标记。
| Q.front()←→Q.back() | ||||||
| -1 | 25 | 18 | 7 | 0 |
|
|
| Q.front()←→Q.back() | ||||||
| 25 | 18 | 7 | 0 | -1 |
|
|
#define NUM 100
int n; //集装箱的数量
int c; //轮船的载重量
int w[NUM]; //集装箱的重量数组
int MaxLoading()
{ queue<int> Q;
Q.push(-1);
int i = 0; int Ew = 0; int bestw = 0; int r = 0;
for(int j=1; j<n; j++)
r += w[j];
while (true) //搜索子空间树
{ //检查左子树
int wt = Ew+w[i];
if (wt<=c) //检查约束条件
{
if (wt>bestw)
bestw = wt;
//加入活结点队列
if (i<n-1)
Q.push(wt);
}
//检查右子树
//检查上界条件
if (Ew+r>bestw && i<n-1)
Q.push(Ew);
Ew = Q.front(); //从队列中取出活结点
Q.pop();
if (Ew==-1) //判断同层的尾部
{
if (Q.empty())
return bestw;
Q.push(-1); //同层结点尾部标志
Ew = Q.front(); //从队列中取出活结点
Q.pop();
i++;
r -= w[i];
}
}
return bestw;
}
②两艘船
问题描述
有两艘船，n 个货箱。第一艘船的载重量是c1，第二艘船的载重量是c2，wi 是货箱i 的重量,且
w1+w2+……+wn≤c1+c2。
我们希望确定是否有一种可将所有n 个货箱全部装船的方法。若有的话，找出该方法 。
问题分析
先看一个实例，当n=3，c1=c2=50，w={10, 40, 40}时，可将货箱1，2装到第1艘船上，货箱3装到第2艘船上。但如果w={20, 40, 40}，则无法将货箱全部装船。所以，该问题可能一解、多解、无解。
虽然是关于两艘船的问题，其实只讨论一艘船的最大装载问题即可。因为当第1艘船的最大装载为bestw时，若w1+w2+……+wn- bestw≤c2 ，则可以确定一种解，否则问题无解。
4.旅行商问题
问题描述
一销售商从n个城市中的某一城市出发，不重复地走完其余n—1个城市并回到原出发点，在所有可能的路径中求出路径长度最短的一条。假定该旅行商从第1个城市出发。
不同于单源最短路径（有向图）
问题分析
在计算限界函数时，令扩展结点i的当前费用为：
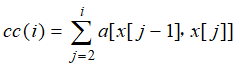
从每个剩余结点出发的最小出边费用的总和为：
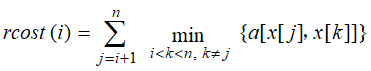
则扩展结点i的限界函数为：
令bestc表示目前为止找到的最佳回路费用和，如果 B(i)≥bestc，则不用把x[i]放入活结点表中，否则放入。具有最小费用B(i)的活结点优先扩展。
问题解决
#define inf 1000000 //∞
#define NUM 100
int n; //图G的顶点数
int a[NUM][NUM]; //图G的邻接矩阵
int NoEdge = inf; //图G的无边标志
int cc; //当前费用
int bestc; //当前的最小费用
struct node
{
//优先队列以lcost为优先级参数
friend bool operator < (const node& a,const node& b)
{
if(a.lcost > b.lcost) return true;
else return false;
}
int lcost; //子树费用的下界
int rcost; //从x[s]～x[n-1]顶点的最小出边
int cc; //当前费用
int s; //当前结点的编号
int x[NUM]; //搜索的路径
};
//定义优先队列
priority_queue <node> H;
int minOut[NUM]; //各个顶点的最小出边费用
int minSum = 0; //最小出边费用之和
//计算各个顶点的最小出边费用
int i, j;
for(i=1; i<=n; i++)
{
int Min = NoEdge;
for(j=1; j<=n; j++)
if( a[i][j]!=NoEdge && (a[i][j]<Min || Min==NoEdge))
Min = a[i][j];
if (Min==NoEdge) return NoEdge; //无回路
minOut[i] = Min;
minSum += Min;
}
//初始化
node E;
for(i=1; i<=n; i++)
E.x[i] = i;
E.s = 1;
E.cc = 0;
E.rcost = minSum;
int bestc = NoEdge;
//搜索排列树
while (E.s<n) //非叶结点
{ //当前扩展结点是叶结点的父结点
if (E.s==n-1)
{ //再加2条边构成回路
//所构成的回路是否优于当前最优解
if (a[E.x[n-1]][E.x[n]]!=NoEdge && a[E.x[n]][1]!=NoEdge && (E.cc+a[E.x[n-1]][E.x[n]]+a[E.x[n]][1]<bestc
|| bestc==NoEdge))
{ //费用更小的回路
bestc = E.cc+a[E.x[n-1]][E.x[n]]+a[E.x[n]][1];
E.cc = bestc;
E.lcost = bestc;
E.s++;
H.push(E);
}
else delete[ ] E.x; //舍弃扩展结点
}
else //搜索树的内部结点
{ //产生当前扩展结点的儿子结点
for (i=E.s+1; i<=n; i++)
if (a[E.x[E.s]][E.x[i]]!=NoEdge)
{ //可行儿子结点
int cc = E.cc+a[E.x[E.s]][E.x[i]];
int rcost = E.rcost-minOut[E.x[E.s]];
int B = cc+rcost; //限界函数B
//子树可能包含最优解
if(B<bestc || bestc==NoEdge)
{ //结点E插入优先队列
node N;
for(j=1; j<=n; j++)
N.x[j] = E.x[j];
N.x[E.s+1] = E.x[i];
N.x[i] = E.x[E.s+1];
N.cc = cc;
N.s = E.s+1;
N.lcost = B;
N.rcost = rcost;
H.push(N);
}
}//完成结点扩展
delete [] E.x;
}
//队列为空时，搜索结束
if(H.empty()) break;
else
{
E=H.top(); //取下一个扩展结点
H.pop();
}
}
if (bestc==NoEdge) return NoEdge; //表示无回路
//输出最优解
for(i=1; i<=n; i++)
printf("%d ", E.x[i]);
printf("\n");
//清空剩余的队列元素
while (!H.empty()) H.pop();
return bestc; //返回最优解
} 5.布线问题
问题描述
印刷电路板将布线区域划分成n×m个方格阵列，如图所示。精确的电路布线问题要求确定连线方格a的中点到方格b的中点的最短布线方案。在布线时，电路只能沿直线或直角布线。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| b |
|
|
|
|
|
|
|
|
|
|
|
问题分析
解此问题的队列式分支限界法从起始位置a开始将它作为第一个扩展结点。与该扩展结点相邻并且可达的方格成为可行结点被加入到活结点队列中，并且将这些方格标记为1，即从起始方格a到这些方格的距离为1。
接着，算法从活结点队列中取出队首结点作为下一个扩展结点，并将与当前扩展结点相邻且未标记过的方格标记为2，并存入活结点队列。这个过程一直继续到算法搜索到目标方格b或活结点队列为空时为止。即加入剪枝的广度优先搜索。
| 移动i | 方向 | Offset[i].row | Offset[i].col |
| 0 | 右 | 0 | 1 |
| 1 | 下 | 1 | 0 |
| 2 | 左 | 0 | -1 |
| 3 | 上 | -1 | 0 |
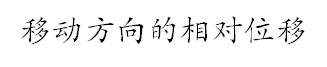
//定义移动方向的相对位移
Position [] offset = new Position [4];
offset[0] = new Position(0, 1); // 右
offset[1] = new Position(1, 0); // 下
offset[2] = new Position(0, -1); // 左
offset[3] = new Position(-1, 0); // 上
//设置边界的围墙
for (int i = 0; i <= size + 1; i++)
{
grid[0][i] = grid[size + 1][i] = 1; // 顶部和底部
grid[i][0] = grid[i][size + 1] = 1; // 左翼和右翼
}
for (int i = 0; i < numOfNbrs; i++)
{ nbr.row = here.row + offset[i].row;
nbr.col = here.col + offset[i].col;
if (grid[nbr.row][nbr.col] == 0)
{ // 该方格未标记
grid[nbr.row][nbr.col] = grid[here.row][here.col] + 1;
if ((nbr.row == finish.row) && (nbr.col == finish.col)) break;
q.put(new Position(nbr.row, nbr.col));
}
}
| 3 | 2 |
|
|
|
|
|
| 2 | 1 |
|
|
|
|
|
| 1 | a | 1 |
|
|
|
|
| 2 | 1 | 2 |
|
| b |
|
|
| 2 | 3 | 4 |
| 8 |
|
|
|
|
| 5 | 6 | 7 | 8 |
|
|
|
| 6 | 7 | 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
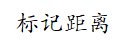
| a |
|
|
|
|
|
|
|
|
|
|
| b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 | 2 |
|
|
|
|
|
|
|
| 2 | 1 |
|
|
|
|
|
|
|
| 1 | a | 1 |
|
|
|
|
|
|
| 2 | 1 | 2 |
|
| b |
|
|
|
|
| 2 | 3 | 4 |
| 8 |
|
|
|
|
|
|
| 5 | 6 | 7 | 8 |
|
|
|
|
|
| 6 | 7 | 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| a |
|
|
|
|
|
|
|
|
|
|
|
|
| b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
扫一扫
2万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
