神经网络损失函数之交叉熵

祝小梦

于 2019-08-14 15:53:59 发布

阅读量3.2k

点赞数 1

原文链接：https://zhuanlan.zhihu.com/p/35709485

版权

交叉熵的函数图：

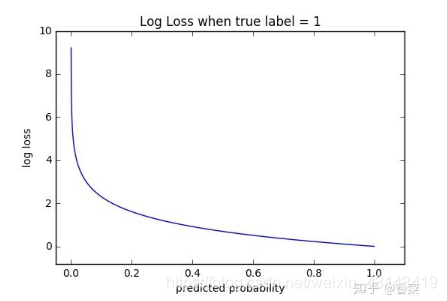
假设我们现在有两个模型，模型1与模型2的预测结果如下图所示：
模型1的预测结果
首先看一下常见的损失函数——均方误差

1.1 Mean Squared Error (均方误差)

均方误差损失也是一种比较常见的损失函数，其定义为： $MSE=\frac{1}{n}\sum_{i}^n(\hat{y_i}-y_i)^2$

模型1： $MSE=\frac{0.54+0.54+1.34}{3}=0.81$

模型2： $MSE=\frac{0.14+0.14+0.74}{3}=0.34$

我们发现，MSE能够判断出来模型2优于模型1，那为什么不采样这种损失函数呢？主要原因是逻辑回归配合MSE损失函数时，采用梯度下降法进行学习时，会出现模型一开始训练时，学习速率非常慢的情况（MSE损失函数）。

有了上面的直观分析，我们可以清楚的看到，对于分类问题的损失函数来说，分类错误率和平方和损失都不是很好的损失函数，下面我们来看一下交叉熵损失函数的表现情况。

1.2 Cross Entropy Error Function（交叉熵损失函数）

1.2.1 表达式

(1) 二分类

在二分的情况下，模型最后需要预测的结果只有两种情况，对于每个类别我们的预测得到的概率为和。此时表达式为：

$\begin{align}L = −[y\cdot log(p)+(1−y)\cdot log(1−p)]\end{align} \\$

其中：
- y——表示样本的label，正类为1，负类为0
- p——表示样本预测为正的概率

(2) 多分类

多分类的情况实际上就是对二分类的扩展：

$\begin{align}L = -\sum_{c=1}^My_{c}\log(p_{c})\end{align} \\$

其中：
- ——类别的数量；
- ——指示变量（0或1）,如果该类别和样本的类别相同就是1，否则是0；
- ——对于观测样本属于类别的预测概率。

现在我们利用这个表达式计算上面例子中的损失函数值：

模型1：
$\begin{align} CEE &= -[0\times log0.3 + 0\times log0.3 + 1\times log0.4] \\ &-[0\times log0.3 + 1\times log0.4 + 0\times log0.3]\\&-[1\times log0.1 + 0\times log0.2 + 0\times log0.7]\\ &= 0.397+ 0.397+ 1 \\ &= 1.8 \end{align} \\$

模型2：

$\begin{align} CEE &= -[0\times log0.1 + 0\times log0.2 + 1\times log0.7] \\ &-[0\times log0.1 + 1\times log0.7 + 0\times log0.2]\\&-[1\times log0.3 + 0\times log0.4 + 0\times log0.3] \\ &= 0.15+ 0.15+ 0.397 \\ &= 0.697 \end{align} \\$

可以发现，交叉熵损失函数可以捕捉到模型1和模型2预测效果的差异。

1.2.2 学习过程

交叉熵损失函数经常用于分类问题中，特别是在神经网络做分类问题时，也经常使用交叉熵作为损失函数，此外，由于交叉熵涉及到计算每个类别的概率，所以交叉熵几乎每次都和sigmoid(或softmax)函数一起出现。

我们用神经网络最后一层输出的情况，来看一眼整个模型预测、获得损失和学习的流程：
1. 神经网络最后一层得到每个类别的得分scores；
2. 该得分经过sigmoid(或softmax)函数获得概率输出；
3. 模型预测的类别概率输出与真实类别的one hot形式进行交叉熵损失函数的计算。
学习任务分为二分类和多分类情况，我们分别讨论这两种情况的学习过程。

1.2.3 损失函数的求导
二分类任务学习过程
（1）计算第一项： $\frac{\partial L}{\partial p}$

- 表示预测为True的概率；

- 表示为True时等于1，否则等于0；

$\begin{aligned} \frac{\partial L}{\partial p} &=\frac{\partial -[y\cdot log(p) + (1-y)\cdot log(1-p)]}{\partial p}\\ &= -\frac{y}{p}-[(1-y)\cdot \frac{1}{1-p}\cdot (-1)] \\ &= -\frac{y}{p}+\frac{1-y}{1-p} \\ \end{aligned} \\$

（2）计算第二项： $\frac{\partial p}{\partial s}$

这一项要计算的是sigmoid函数对于score的导数，我们先回顾一下sigmoid函数和分数求导的公式：

$p_c = \sigma(s_c) = \frac{1}{1+e^{s_c}} \\$
$f'(x) = \frac{g(x)}{h(x)}=\frac{g'(x)h(x)-g(x){h}'(x)}{h^2(x)} \\$

$\begin{aligned} \frac{\partial p}{\partial s} &= \frac{1'\cdot (1+e^{s})-1\cdot (1+e^{s})'}{(1+e^{s})^2} \\ &= \frac{0\cdot (1+e^{s})-1\cdot e^{s}}{(1+e^{s})^2} \\ &= \frac{-e^{s}}{(1+e^{s})^2} \\ &= \frac{1}{1+e^{s}}\cdot \frac{-e^{s}}{1+e^{s}} \\ &= \sigma(s)\cdot [1-\sigma(s)] \\ \end{aligned} \\$

（3）计算第三项： $\frac{\partial s}{\partial w_i \\}$

一般来说，scores是输入的线性函数作用的结果，所以有：
$\frac{\partial s}{\partial w_i}=x_i \\$

（4）计算结果 $\frac{\partial L}{\partial w_i}$

$\begin{aligned} \frac{\partial L}{\partial w_i} &= \frac{\partial L}{\partial p}\cdot \frac{\partial p}{\partial s}\cdot \frac{\partial s}{\partial w_i} \\ &= [-\frac{y}{p}+\frac{1-y}{1-p}] \cdot \sigma(s)\cdot [1-\sigma(s)]\cdot x_i \\ &= [-\frac{y}{\sigma(s)}+\frac{1-y}{1-\sigma(s)}] \cdot \sigma(s)\cdot [1-\sigma(s)]\cdot x_i \\ &= [-\frac{y}{\sigma(s)}\cdot \sigma(s)\cdot (1-\sigma(s))+\frac{1-y}{1-\sigma(s)}\cdot \sigma(s)\cdot (1-\sigma(s))]\cdot x_i \\ &= [-y+y\cdot \sigma(s)+\sigma(s)-y\cdot \sigma(s)]\cdot x_i \\ &= [\sigma(s)-y]\cdot x_i \\ \end{aligned} \\$

可以看到，我们得到了一个非常漂亮的结果，所以，使用交叉熵损失函数，不仅可以很好的衡量模型的效果，又可以很容易的的进行求导计算。

1.2.4 优缺点

在用梯度下降法做参数更新的时候，模型学习的速度取决于两个值：一、学习率；二、偏导值。其中，学习率是我们需要设置的超参数，所以我们重点关注偏导值。从上面的式子中，我们发现，偏导值的大小取决于和 $[\sigma(s)-y]$ ，我们重点关注后者，后者的大小值反映了我们模型的错误程度，该值越大，说明模型效果越差，但是该值越大同时也会使得偏导值越大，从而模型学习速度更快。所以，使用逻辑函数得到概率，并结合交叉熵当损失函数时，在模型效果差的时候学习速度比较快，在模型效果好的时候学习速度变慢。

此外，从图像中可以看出该函数是凸函数，求导时能够得到全局最优值。

感谢[https://zhuanlan.zhihu.com/p/35709485]的分析(https://zhuanlan.zhihu.com/p/35709485)

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。