
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>
using namespace std;
int symmetry(char c[])
{
int len=strlen(c);
int i=0;
int j=len-1;
while(i<j) //出错
{
if(c[i]==c[j])
{
i++;
j--;
}
else
{
return 0;
}
}
return 1;
}
int main()
{
int n=256;
int i,j;
int N;
char c[10000];
for(i=1;i<n;i++)
{
N=i*i;
j=0; //出错
while(N!=0)
{
c[j++]=N%10+'0';
N=N/10;
}
c[j]='\0';
if(symmetry(c))
{
printf("%d\n",i);
}
}
return 0;
}
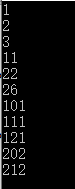





 本文介绍了一种使用C++编程语言生成并判断回文数的方法。通过算法,程序能够生成指定范围内的所有回文数,展示了字符串操作、循环结构及函数调用等基本编程技巧。适用于初学者理解和实践回文数的概念。
本文介绍了一种使用C++编程语言生成并判断回文数的方法。通过算法,程序能够生成指定范围内的所有回文数,展示了字符串操作、循环结构及函数调用等基本编程技巧。适用于初学者理解和实践回文数的概念。
















 480
480

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








