#include <stdio.h>
#include <stdlib.h>
#include <iostream>
using namespace std;
bool hasGroupsSizeX(int* deck, int deckSize)
{
int i,j,x;
int num=1;
int max[100];
int temp;
for(i=0; i<deckSize; i++)
{
temp=deck[i];
j=i-1;
while(j>=0&&temp<deck[j])
{
deck[j+1]=deck[j];
--j;
}
deck[j+1]=temp;
}
for(i=0; i<deckSize; i++)
{
cout<<deck[i]<<" ";
}
cout<<endl;
if(deckSize<=1)
{
return 0;
}
for(x=2; x<=deckSize; x++)
{
j=0;
for(i=1; i<=deckSize; i++)
{
if(deck[i]==deck[i-1])
{
num=num+1;
}
else
{
cout<<"输出的num值为:"<<num<<endl;
max[j]=num;
j=j+1;
num=1;
}
}
cout <<"max数组如下:"<<endl;
for(i=0; i<j; i++)
{
cout<<max[i]<<" ";
}
cout<<endl;
for (i = 0; i <j; i++)
{
if (max[i] % x == 0)
{
continue;
}
else
{
break;
}
}
if(i==j)
{
return 1;
}
}
return 0;
}
int main()
{
int deck[100000];
int deckSize;
cin>>deckSize;
int i;
for(i=0; i<deckSize; i++)
{
cin>>deck[i];
}
if(hasGroupsSizeX(deck,deckSize))
{
cout<<"可以成功划分!"<<endl;
}
else
{
cout<<"卡牌划分失败!"<<endl;
}
}






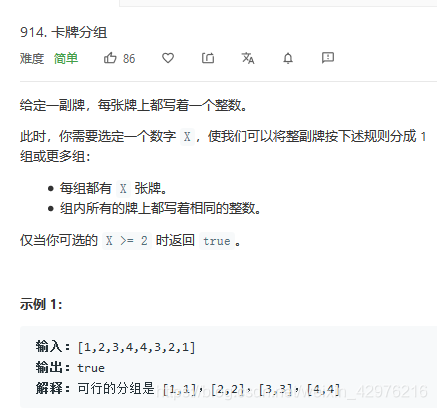
 本文详细解析了一个使用C++实现的卡牌游戏算法,该算法通过直接插入排序对卡牌进行排序,并检查是否能将卡牌按特定大小X进行分组。文章深入探讨了算法的具体实现细节,包括数组操作、条件判断及循环结构的应用。
本文详细解析了一个使用C++实现的卡牌游戏算法,该算法通过直接插入排序对卡牌进行排序,并检查是否能将卡牌按特定大小X进行分组。文章深入探讨了算法的具体实现细节,包括数组操作、条件判断及循环结构的应用。
















 282
282

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








