第五章树——哈夫曼树的创建与最优二叉树的带权路径和

最新推荐文章于 2024-04-25 15:04:42 发布

原创

最新推荐文章于 2024-04-25 15:04:42 发布 · 762 阅读

6 ·

CC 4.0 BY-SA版权

本文详细介绍了如何使用C++实现哈夫曼树的创建过程，通过选取权值最小的两个节点构建新的父节点，逐步形成一棵最优二叉树。文中还解释了带权路径长度（WPL）的概念及其计算方法。

第五章树—哈夫曼树的创建与最优二叉树的带权路径和

数据结构基础代码（严蔚敏人邮教育出版社）
哈夫曼树 带权路径长度最短的树。
假设给叶子节点A、B、C、D它们的权值是2、4、5、7.则构成的哈夫曼树如下图所示：
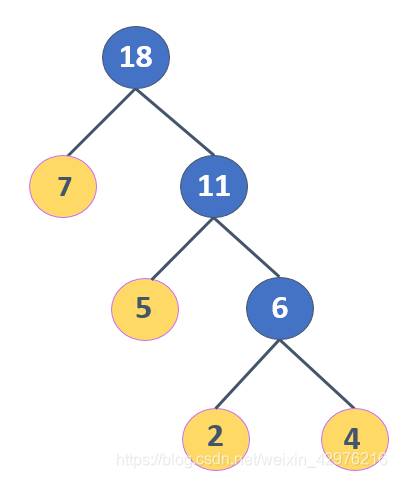
在这里插入图片描述
带权路径长度（WPL）
树中所有叶子结点的带权路径长度和，其中叶子结点的带权路径是该结点到树根之间路径长度与结点上权的乘积。
上图所示的带权路径长度是：WPL=23+43+52+71=35

//哈夫曼树的创建
#include <stdio.h>
#include<stdlib.h>
#include<iostream>
using namespace std;

typedef struct
{
   
   
    int weight;
    int parent,lchild,rchild;
}HTNode,*HuffmanTree;

void Select(HuffmanTree HT,int n,int &s1,int &s2)   // n表示当前可以构成新的二叉树的根节点个数。
{
   
   
    int minum;                             //定义一个临时变量保存最小值。
    int i;
    for(i=1;i<=n;i++)                     //从给定的根节点中，找到双亲为0，并且权值最小的第一个根节点。
    {
   
   
        if(HT[i].parent==0)
        {
   
   
            minum=i;
            break