递归由浅到深(一) 递归遍历数组求和的java实现

递归由浅到深(一) 递归遍历数组求和的java实现

递归的学习从大一数据结构开始到现在也差不多两年，一直对概念模糊，几乎不曾使用。接着这次重新学习数据结构，对递归进行一次由浅到深的学习。

递归的实质： 将原来的问题，转化为更小的一部分

例如数组求和 sum（arr[0—n-1]）

sum(arr[0—n-1] = arr[0] + sum(arr[1—n-1]) // 再此我们将问题转换为更小的同一问题
sum(arr[n-1—n-1] = arr[n-1] + sum(arr[]) //这便是最基本的问题 也是递归的终止条件

下面了解一下理论知识 ， 引用数据结构书上原话

对于类似这种的问题，若能够分解成几个相对简单且解法相同或类似的子问题来求解，便称为递归求解。 例如上面 对数组arr[0—n] 的求和 可以分为 arr[0] + arr[1—n-1] ，然后再进一步分解进行求解，这种分解->求解的策略叫做‘分治法’

采用‘分治法’需要满足以下三个条件

1. 能够将一个问题转变为一个新问题 ，而新问题与原问题的解法相同或类似 ， 不同的仅是处理的对象，而且这些问题处理对象更小且变化有规律
2. 可以通过上述转化使问题简化
3. 必须有一个明确的递归出口，或者是递归的边界

那么有了以上理论和举例的伪代码我们来看利用递归遍历数组求和的实现（java）

public class Sum {
    /**
     * 递归遍历数组求和
     * @param arr
     * @return
     */
    public static int sum(int[] arr){
        return sum(arr , 0);
    }


    /**
     * 计算arr[l...n]这个区间内的所有数组之和
     * @param arr : 带遍历数组
     * @param l ： 遍历起点此例中我们默认从0开始
     * @return
     */
    private static int sum(int[] arr , int l){
        if (l == arr.length)
            return 0;
        return arr[l] + sum(arr , l+1);
    }

	 /**
     * 测试方法
     */
    public static void main(String[] args) {
        int[] nums = {1 ,2 ,3 ,4,5 };
        int n = sum(nums);
        System.out.println(n);

    }
}

我们对 int n = sum(nums); 打断点调试可以看到第一次return arr[0] + sum(arr ,1 ); 便是将从这个问题拆分成一个更下的问题

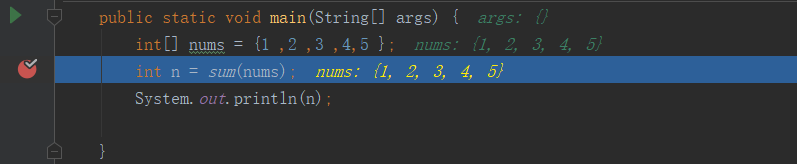
tips ：我对第一个sum()方法设为public 对第二个sum（）方法设为私有 。这样对具体功能的底层实现对用户进行屏蔽 用户只需要知道有这样一个方法可以实现即可不需要知道具体的底层实现

再进一步分解

此时我们来到了递归出口，即 l == arr.length 之后return 0； 跳出递归

这也就是递归遍历数组求和 的具体实现过程

个人补充

在对于递归刚学习的之初一直无法理解return 为什么最后会是15
通过调试之后 可以发现 return 语句最后返回的是
return arr[0]+arr[1]+arr[2]+arr[3]+arr[4]+0 
 即
return 1+2+3+4+5+0
我们可以将sum()方法return arr[l] + sum(arr , l+1); 
改为 return 1 + sum(arr , l+1);
可以看到结果变为 5 

总结 ： 递归的本质就是将一个大问题拆分为类似的小问题 ，而递归的实现需要一个递归的出口也可以称为递归的边界。