统计学之基础知识（一）

参考资料：可汗学院统计学、深入浅出统计学

统计学基础知识

1.平均数
平均值就是用数据之和除以数据的个数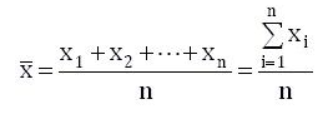
2.方差
偏差=数据的数值-平均值
方差=[（偏差的平方）的合计]/（数据数）

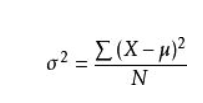
3.标准差
标准差=方差的均方根
均值体现了平均程度，标准差体现数值的变异程度。

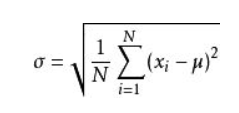
补充：标准分
z分=$$\frac{X-\mu }{\theta }$$

数据类型有哪些？
在统计学中，统计数据主要可分为四种类型，分别是定类数据，定序数据，定距数据，定比变量。
1.定类数据（Nominal）：名义级数据，数据的最低级，表示个体在属性上的特征或类别上的不同变量，仅仅是一种标志，没有序次关系。例如， ”性别“，”男“编码为1，”女“编码为2。
2.定序数据（Ordinal）:数据的中间级，用数字表示个体在某个有序状态中所处的位置，不能做四则运算。例如，“受教育程度”，文盲半文盲=1，小学=2，初中=3，高中=4，大学=5，硕士研究生=6，博士及其以上=7。
3.定距数据（Interval）:具有间距特征的变量，有单位，没有绝对零点，可以做加减运算，不能做乘除运算。例如，温度。
4.定比变量（Ratio）:数据的最高级，既有测量单位，也有绝对零点，例如职工人数，身高。

箱线图

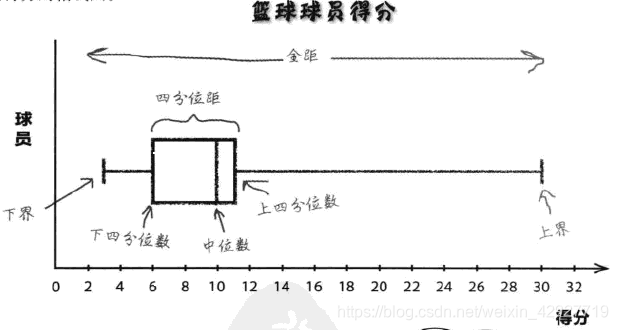
如果箱线图是对称的，那么数据则有可能也是相当对称的。箱线图的弊端是忽略了数据出现的频率，只是单纯考虑数据的差距等。

几何分布、二项分布、泊松分布

几何分布

几何分布满足条件：

几何分布方差、均值计算公式：

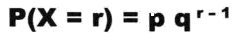
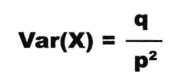
二项分布

二项分布是指在只有两个结果的n次独立的伯努利试验中，所期望的结果出现次数的概率。在单次试验中，结果A出现的概率为p，结果B出现的概率为q，p+q=1。那么在n=10，即10次试验中，结果A出现0次、1次、……、10次的概率各是多少呢？这样的概率分布呈现出什么特征呢？这就是二项分布所研究的内容。
二项分布均值和方差计算公式：

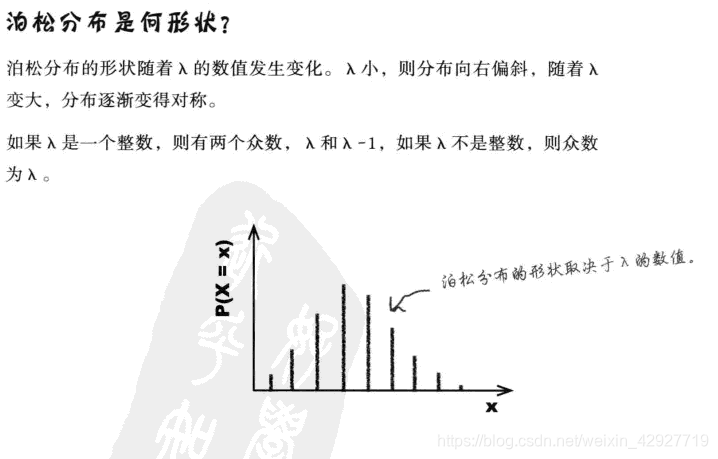
泊松分布

大数定律

定义 1 若ξ1, ξ2, …, ξn, … 是随机变量序列，令

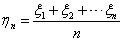
若存在常数序列 a1, a2, …, an, … 对任何的正数ε，恒有

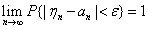
则称序列 {ξn} 服从大数定律（或大数法则）
定义 2 对于独立随机变量序列ξ1, ξ2, …, ξn, … 假定 Eξn 和 Dξn 都存在，令

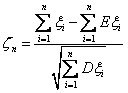
若

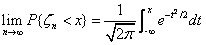
则称序列 {ξn} 服从中心极限定理（Central Limit Theorem）。

大数定理和中心极限定律的区别

• 大数定律是说，n只要越来越大，把这n个独立同分布的数加起来去除以n得到的这个样本均值（也是一个随机变量）会依概率收敛到真值$\epsilon$，但是样本均值的分布是怎样的我们不知道。
• 中心极限定理是说，n只要越来越大，这n个数的样本均值会趋近于正态分布，并且这个正态分布以u为均值，$\frac{{\Sigma }^2}{n}$为方差。
• 综上所述，这两个定律都是在说样本均值性质。随着n增大，大数定律说样本均值几乎必然等于均值。中心极限定律说，他越来越趋近于正态分布。并且这个正态分布的方差越来越小。直观上来讲，想到大数定律的时候，你脑海里浮现的应该是一个样本，而想到中心极限定理的时候脑海里应该浮现出很多个样本。

正态分布

正态分布的概率密度函数
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$
标准化后：
$$f(x)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}$$
正态分布曲线：

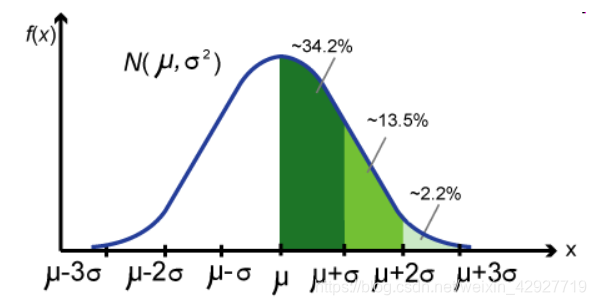
参考博客

沈波 https://blog.youkuaiyun.com/shenbo2030/article/details/20040455
如何理解二项分布
大数定律和中心极限定律
统计之都