CCPC2019哈尔滨站（E - Exchanging Gifts）（拓扑图+map合并）

CCPC2019哈尔滨站（E - Exchanging Gifts）（拓扑图+map合并）

time limit per test1 second
memory limit per test512 megabytes
inputstandard input
outputstandard output
judge：点我跳转

Description

After the dress rehearsal of CCPC Harbin Site 2019, $m$ contestants are still in the contest arena. They are taking photos, discussing the problems, and exchanging gifts.

Initially, everyone has exactly one gift in their hand. Note that some contestants may have the same type of gifts. Specifically, the type of the gift in the $i$-th contestant’s hand can be represented as a positive integer $g_i$. Two contestants $i$ and $j(1\le i,j\le m)$ share the same type of gifts if and only if $g_i=g_j$ holds.

There can be many rounds of gift exchanging between these $m$ contestants. In each round, two contestants may exchange their gifts with each other. Note that a pair of contestants can exchange gifts multiple times if they like. In the end, there will still be exactly one gift in each contestant’s hand.

Let’s denote $h_i$ as the type of gift in the $i$-th contestant’s hand in the end. If $g_i\ne h_i$ holds, the $i$-th contestant will be happy, because they have a different type of gift, otherwise they will be unhappy. Your task is to write a program to help them exchange gifts such that the number of happy contestants is maximized. For example, if $g=[3,3,2,1,3]$ and $h=[1,2,3,3,3]$, there will be $4$ happy contestants.

Since $m$ can be extremely large, you will be given $n$ sequences $s_1,s_2,\dots ,s_n$, and the sequence $g$ is equal to $s_n$. The $i$-th $(1\le i\le n)$ sequence will be given in one of the following two formats:

“1 k q[1…k]” ($1\le k\le 10^6$, $1\le q_i\le 10^9$): It means $s_i=[q_1,q_2,\dots ,q_k]$.
“2 x y” ($1\le x,y\le i-1$): It means $s_i=s_x+s_y$. Here “$+$” denotes concatenation of sequences, for example $[3,3,2]+[2,2,3,3]=[3,3,2,2,2,3,3]$.

Input

The input contains multiple cases. The first line of the input contains a single integer $T$ ($1\le T\le 10000$), the number of cases.

For each case, the first line of the input contains a single integer $n$ ($1\le n\le 10^6$), denoting the number of sequences. Each of the next $n$ lines describes a sequence in one of the two formats defined in the problem statement, where the $i$-th ($1\le i\le n$) line describes the sequence $s_i$.

It is guaranteed that the sum of all $n$ over all cases does not exceed $10^6$, and the sum of $k$ over all cases does not exceed $10^6$. It is also guaranteed that no sequence has a length that exceeds $10^{18}$.

Output

For each case, print a single line containing a single integer denoting the maximum number of happy contestants.

Example

input

2
1
1 5 3 3 2 1 3
3
1 3 3 3 2
1 4 2 2 3 3
2 1 2

output

4
6

题解

按照惯例，先奉图一张：


题意有点绕，大概是这样：

就是说如果有一个序列经过重新排列后，一个数字和以前这个位子的数字不同的话，快乐值就会+1，问你一个序列最大的快乐值是多少。其实很简单，我们只需要判断出现次数最多的那个数字的次数 $m$ 有没有超过 $n/2$ 即可，如果没有，那么经过重新排列后每个位子的数字都可以和以前的数字不同，快乐值就是 $n$ ；如果超过了，那么最大的快乐值就会是 $2n-2m$ 。

可是问题出在哪了呢？就是题目不直接给你那个序列，因为它太长了，最大长度可以是 $10^{18}$……

题目会给你 $n$ 个序列，你要求的是第 $n$ 个序列（即 $s[n-1]$ ）的快乐值；有的序列是直接告诉你元素的，有的序列是由前面的某两个序列合并在一起组成的，这道题难就难在如何高效地“合并”这些序列，最终求得目标序列。

当然，最直接的思路肯定是用 $map$ 维护，然后 $map$ 暴力维护 $T$ 在了 $test2$ .

优化一下合并的过程，从传对象变成传指针，一切操作都在已有的对象上进行， $T$ 在了 $test3$ .

改变思路，从正向合并变成反相递推，建立一个图进行 $dfs$ 搜索需要哪些基本的序列，找完之后统一合并， $T$ 在了 $test4$ .

不再暴力 $dfs$ 了，改成求拓扑图，先 $bfs$ 找出所有有用的序列的入度，这个“有用”指的是被用来合并最后一个序列的序列。然后再 $bfs$ 求拓扑图，中间合并这些序列， $T$ 在了 $test5$ .

最后换了一个快读板子， $A$ 了（手动滑稽）。

下面讲解一些如何建立拓扑图和如何求解拓扑图。

假如这里有一些序列，序列n是由序列4和序列3构成的，序列n-1是由序列4和序列2构成的，序列3是由序列1和序列2构成的。好复杂的样子……

但是画成图就好看多了：

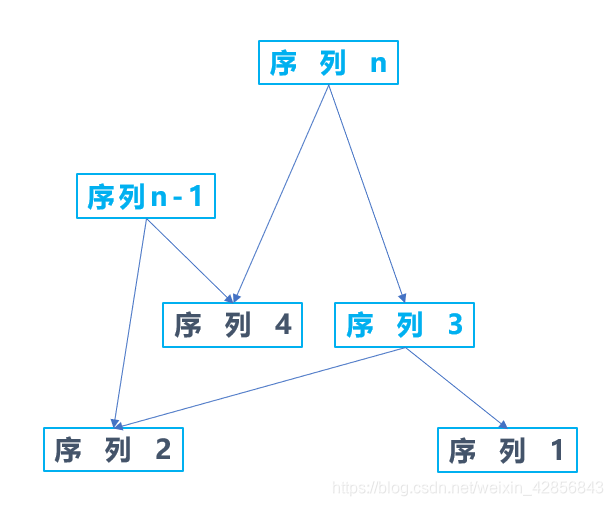
可以看到，真实的序列只有1、2和4 ，其他的都是需要组合而成的；而仔细观察发现虽然序列n-1也是一个序列，但是它对序列n的合成没有贡献。所以我们认为它对4和2的入度是无效的；我们只统计有效的入度之后，图是这样的：

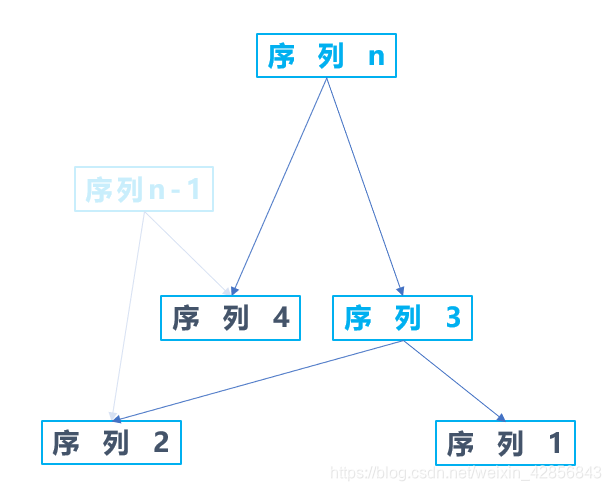
从序列n开始往下bfs搜索，往下寻找的深度即是这个序列的重用次数；只有当路径上的点的入度为0时我们才push这个点继续往前走。最后就完成了一个拓扑图的求解。而每一次合并两个序列我们只需要更新一下map的数字出现的次数即可，最后我们从map里统计出现次数最多的那个数字。

代码

#pragma GCC optimize(2)
#include <bits/stdc++.h>
#define maxn 1000006
#define _for(i, a) for(LL i = 0; i < (a); ++i)
#define _rep(i, a, b) for(LL i = (a); i <= (b); ++i)
using namespace std;
typedef long long LL;

inline char nc() {
	static char buf[1000000], *p1 = buf, *p2 = buf;
	return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++;
}
template <typename _Tp> inline void read(_Tp&sum) {
	char ch = nc(); sum = 0;
	while (!(ch >= '0'&&ch <= '9')) ch = nc();
	while (ch >= '0'&&ch <= '9') sum = (sum << 3) + (sum << 1) + (ch - 48), ch = nc();
}

struct poi {
	LL l, r;
	poi() {}
	poi(LL l, LL r) :l(l), r(r) {}
};

vector< vector<LL> > vm;
poi G[maxn];
LL T, n;
map< LL, LL > an;
LL vis[maxn], cnt[maxn], in[maxn];

void init() {
	vm.clear();
	an.clear();
	_for(i, n) cnt[i] = 0, vis[i] = 0, in[i] = 0;
}

void bfs_in(LL s) {
	queue<LL> q;
	q.push(s);
	vis[s] = 1;
	while (q.size()) {
		LL t = q.front();
		q.pop();
		if (G[t].r != -1) {
			LL l = G[t].l, r = G[t].r;
			in[l]++; in[r]++;
			if (!vis[l]) q.push(l), vis[l] = 1;
			if (!vis[r]) q.push(r), vis[r] = 1;
		}
	}
}

void bfs(LL s) {
	queue<LL> q;
	cnt[s] = 1;
	q.push(s);
	while (q.size()) {
		LL t = q.front();
		q.pop();
		if (G[t].r != -1) {
			LL l = G[t].l, r = G[t].r;
			cnt[l] += cnt[t];
			cnt[r] += cnt[t];
			if (--in[l] == 0) q.push(l);
			if (--in[r] == 0) q.push(r);
		}
		else {
			for (LL &x : vm[G[t].l]) {
				an[x] += cnt[t];
			}
		}
	}
}

void sol() {
	init();
	_for(i, n) {
		LL op;
		read(op);
		poi t;
		if (op == 1) {
			LL len, x;
			read(len);
			G[i].l = vm.size();
			G[i].r = -1;
			vm.resize(vm.size() + 1);
			_for(j, len) {
				read(x);
				vm.back().emplace_back(x);
			}
		}
		else {
			LL x, y;
			read(x), read(y);
			G[i].l = x - 1;
			G[i].r = y - 1;
		}
	}
	bfs_in(n - 1);
	bfs(n - 1);
	LL ans = 0, num = 0;
	for (auto &it : an) {
		num += it.second;
		ans = max(ans, it.second);
	}
	printf("%lld\n", ans > num / 2 ? 2 * num - 2 * ans : num);
}

int main() {
	//ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	//freopen("in.txt", "r", stdin);

	while (cin >> T) {
		_for(i, T) {
			read(n);
			sol();
		}
	}
	return 0;
}