布隆过滤器 浅析 - 20181119

一.引言

• BloomFilter算法，是一种大数据排重算法。牺牲精度，达到高效利用空间的目的。
• 可以过滤无效请求，恶意攻击。
• 只记录特征，不记录原始数据
• 查询特征值不存在，就代表没有数据；特征值存在，则代表数据可能存在。

二.优缺点

• 优点：
  1.查询时间复杂度 O(k) 一个较小的常数
  2.极度节约空间
  3.不存储数据本身，对源数据有一定保密性
• 缺点：
  1.有一定误差
  2.不能删除

三.详解

1.布隆过滤器
布隆过滤器，它是一种节省空间的概率数据结构（就是 位图 + 哈希）。主要功能是检查一个元素是否在给定的集合中。说它是一种概率数据结构是因为每次对它的查询会返回 2 种结果；一种是“可能在集合中”，也就是说它可能会误报，这个误报是有一定概率的，后面我们会详细介绍这个概率。另一种结果是“一定不在集合中”，这个结果是肯定的，也就是不会漏报。

2.位图（bitmap）
布隆过滤器=位图+哈希。那么什么是位图呢？位图（bitmap）我们可以理解为是一个 bit 数组，每个元素存储数据的状态（由于每个元素只有 1 bit，所以只能存储 0 或 1 这 2 种状态）适用于数据量超大，但是数据的状态很少的情况。比如判断一个整数是否在给定的超大的整数集中。
3.
它先定义一个长度为 m 的位图数组，初始值都为 0 ，然后定义 k 个不同的符合随机分布的哈希函数，添加一个元素的时候通过 k 个哈希函数得到 k 个 hash 值，将它们映射到位图数组中（当然计算出来的 hash 值可能超过了 m，那么就需要扩容，java 中 BitSet 的扩容方案是 Math.max(2 * 当前长度, 计算出来的 hash 值); ）

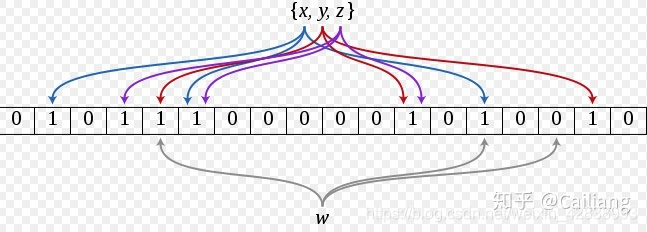
4.
查询的时候把这个元素作为 K 个哈希函数的输入，得到 K 个数组的位置。如果这些位置中有任意一个是 0，说明元素肯定不在集合中。如果这些位置全部为 1，那么该元素很可能是在集合中，因为也有可能这些位置是被其他元素设置的。