八大排序算法总结【C语言】

最新推荐文章于 2024-12-13 21:55:30 发布
原创 最新推荐文章于 2024-12-13 21:55:30 发布 · 550 阅读 · 14 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

这篇博客总结了八种常见的排序算法：简单选择排序、冒泡排序、快速排序、插入排序、希尔排序、堆排序、归并排序和基数排序。通过C语言的代码实现，配合排序过程的说明，帮助读者理解和掌握各种排序方法的工作原理。每个算法都有对应的测试代码和运行现象描述，方便读者实践和理解。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

这里写的比较简单，仅列出思想和测试代码。如果想更深入了解或者看完下面的内容还不理解，可以参考链接：排序算法总结 排序动图演示

测试环境： VC++ 6.0

一.简单选择排序

思想：
每一趟从待排序的数据元素中选出最小（最大）的元素，顺序放在待排序的数列最前，直到全部待排序的数据元素全部排完。
这里写图片描述
代码

#include<stdio.h>
void SelectionSort(int *num,int n) 
{
    int i = 0;
    int min = 0;
    int j = 0;
    int tmp = 0;
    for (i = 0;i < n-1;i++) 
    {
        min = i;
        //每次将min置成无序组起始位置元素下标 
        for (j = i;j < n;j++)//遍历无序组，找到最小元素。 
        {
            if(num[min]>num[j]) 
            {
                min = j;
            }
        }
        if(min != i)//如果最小元素不是无序组起始位置元素，则与起始元素交换位置 
        {
            tmp = num[min];
            num[min] = num[i];
            num[i] = tmp;
        }
    }
}
int main() 
{
    int num[6] = {5,4,3,2,9,1};
    int i = 0;
    printf("=========简单选择排序=============\n");
    printf("排序前数组为:\n");
    for (i = 0;i < 6;i++) 
    {
        printf("%d ",num[i]);
    }
    printf("\n");
    SelectionSort(num,6);
    printf("排序后数组为:\n");
    //这里需要将数列元素个数传入。有心者可用sizeof在函数内求得元素个数。 
    for (i = 0;i < 6;i++) 
    {
        printf("%d ",num[i]);
    }
    printf("\n");
    return 0;
}

现象：
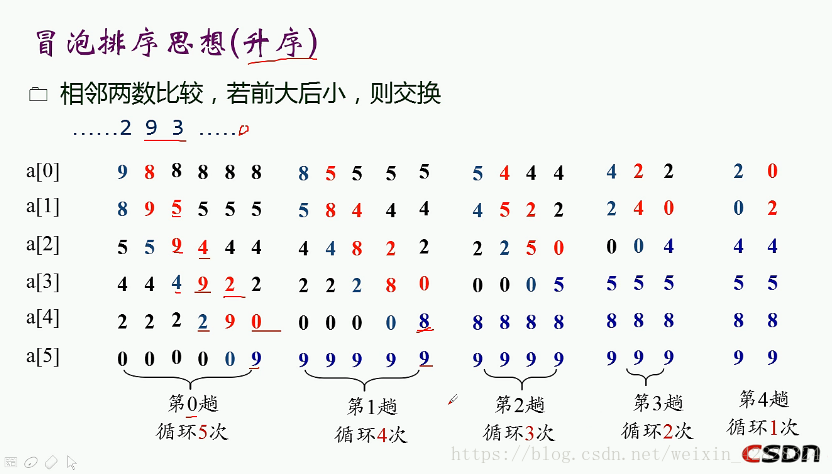
这里写图片描述

二.冒泡排序

思想：
这里写图片描述
代码：

#include <stdio.h>
#define SIZE 10
int main() 
{
    int a[SIZE]={12 ,43,9,13,67,98,101,89,3,35};
    //十个数的无序数列
    int i,j,t;
    printf("===============冒泡排序=================\n");
    printf("排列前的数列是：\n");
    for (i=0;i<10;i++) 
    {
        printf("%d ",a[i]);
    }
    printf("\n");
    for (i=0;i<10-1;i++)//n个数的数列总共扫描n-1次 
    {
        for (j=0;j<10-i-1;j++)//每一趟扫描到a[n-i-2]与a[n-i-1]比较为止结束 
        {
            if(a[j]>a[j+1])//后一位数比前一位数小的话，就交换两个数的位置（升序） 
            {
                t=a[j+1];
                a[j+1]=a[j];
                a[j]=t;
            }
        }
    }
    printf("排列好的数列是：\n");
    for (i=0;i<10;i++) 
    {
        printf("%d ",a[i]);
    }
    printf("\n");
    return 0;
}

现象：
这里写图片描述

三.快速排序

快速排序的思想：
1.先把整个序列分成两块，一块都大于某个数。一块都大于某个数。
2.再将分开的两块继续分，直到每块均为一个数。
分割的方法是填坑。
先从右后左，后从左往右，参考此篇[文章]。(https://blog.youkuaiyun.com/morewindows/article/details/6684558)
代码如下：
填坑：

int AdjustArray(int s[], int l, int r) //返回调整后基准数的位置，l是排序开始的位置，r是排序结束的位置。 
{
    int i = l, j = r;
    //先将l和r保存下来。
    int x = s[l];
    //s[l]即s[i]就是第一个坑
    while (i < j) 
    {
        // 从右向左找小于x的数来填s[i]
        while(i < j && s[j] >= x) 
                    j--;
        if(i < j) 
        {
            s[i] = s[j];
            //将s[j]填到s[i]中，s[j]就形成了一个新的坑
            i++;
        }
        // 从左向右找大于或等于x的数来填s[j]
        while(i < j && s[i] < x)
                    i++;
        if(i < j) 
        {
            s[j] = s[i];
            //将s[i]填到s[j]中，s[i]就形成了一个新的坑
            j--;
        }
    }
    //退出时，i等于j。将x填到这个坑中。
    s[i] = x;
    return i;
}

分冶的代码


void quick_sort1(int s[], int l, int r) 
{
    if (l < r) 
    {
        int i = AdjustArray(s, l, r);
        //先成挖坑填数法调整s[]
        quick_sort1(s, l, i - 1);
        // 递归调用 
        quick_sort1(s, i + 1, r);
    }
}

完整子函数代码，写在检测l 是否 < r 那里即可。

//快速排序
void quick_sort(int s[], int l, int r) 
{
    if (l < r) 
    {
        //Swap(s[l], s[(l + r) / 2]); //将中间的这个数和第一个数交换 参见注1
        int i = l, j = r, x = s[l];
        while (i < j) 
        {
            while(i < j && s[j] >= x) // 从右向左找第一个小于x的数
            j--;
            if(i < j) 
                            s[i++] = s[j];
            while(i < j && s[i] < x) // 从左向右找第一个大于等于x的数
            i++;
            if(i < j) 
                            s[j--] = s[i];
        }
        s[i] = x;
        quick_sort(s, l, i - 1);
        // 递归调用 
        quick_sort(s, i + 1, r);
    }
}

完整代码：

#include<stdio.h>
void quick_sort(int s[], int l, int r) 
{
    if (l < r) 
    {
        //Swap(s[l], s[(l + r) / 2]); //将中间的这个数和第一个数交换 参见注1
        int i = l, j = r, x = s[l];
        while (i < j) 
        {
            while(i < j && s[j] >= x) // 从右向左找第一个小于x的数
            j--;
            if(i < j) 
            {
                s[i++] = s[j];
            }
            while(i < j && s[i] < x) // 从左向右找第一个大于等于x的数
            i++;
            if(i < j) 
            {   
                s[j--] = s[i];
            }
        }
        s[i] = x;
        quick_sort(s, l, i - 1);
        // 递归调用 
        quick_sort(s, i + 1, r);
    }
}
void main() 
{
    int i;
    int a[10]={9,8,7,6,5,4,3,2,1,9};
    printf("=============快速排序===============\n");
    printf("排序前的数组");
    for (i=0;i<10;i++) 
    {
        printf("%d ",a[i]);
    }
    printf("\n");
    quick_sort(a, 0, 9);
    printf("排序后的数组");
    for (i=0;i<10;i++) 
    {
        printf("%d ",a[i]);
    }
    printf("\n");
}

现象：
这里写图片描述

四.插入排序

排序思路：每次将一个待排序的元素与已排序的元素进行逐一比较，直到找到合适的位置按大小插入。
代码：

#include <stdio.h>
void Insertion_Sort(int a[],int n) 
{
    int i,j;
    for (i=1;i<n;i++) 
    {
        int temp=a[i];
        for (j=i;j>0&&a[j-1]>temp;--j) 
        {
            a[j]=a[j-1];
        }
        a[j]=temp;
    }
}
int main() 
{
    int a[]={1,3,63,5,78,9,12,52,8};
    int n=sizeof(a)/sizeof(int),i;
    Insertion_Sort(a,n);
    for (i=0;i<n;i++)
            printf("%d ",a[i]);
    return 0;
}

现象：

这里写图片描述

五.希尔排序

希尔排序为插入排序的优化，解决了插入排序一次只能移动一个位置的问题。

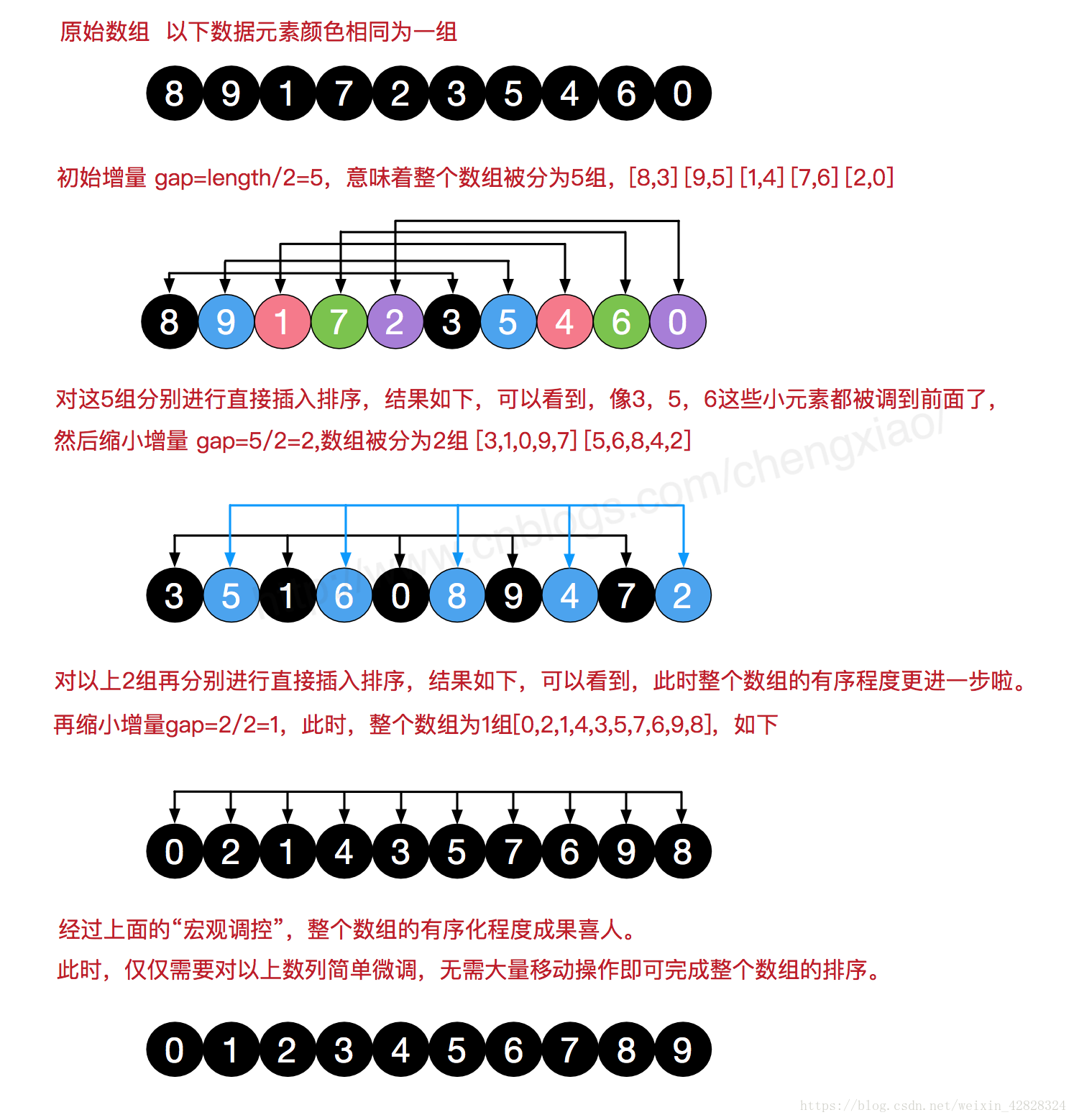
这里写图片描述
代码如下

#include <stdio.h>
#include <stdlib.h>
void ShellSort(int a[], int length) 
{
    int increment;
    int i,j;
    int temp;
    for (increment = length/2; increment > 0; increment /= 2) //用来控制步长,最后递减到1 
    {
        // i从第step开始排列，应为插入排序的第一个元素
        // 可以先不动，从第二个开始排序
        for (i = increment; i < length; i++) 
        {
            temp = a[i];
            for (j = i - increment; j >= 0 && temp < a[j]; j -= increment) 
            {
                a[j + increment] = a[j];
            }
            a[j + increment] = temp;
            //将第一个位置填上
        }
    }
}
int main() 
{
    int i, j;
    int a[] = {5, 18, 151, 138, 160, 63, 174, 169, 79, 200};
    printf("==============希尔排序===============\n\n");
    printf("待排序的序列是: \n");
    for (i = 0; i < 10; i++) 
    {
        printf("%d ", a[i]);
    }
    ShellSort(a, 10);
    printf("\n排序后的序列是: \n");
    for (j = 0; j < 10; j++) 
    {
        printf("%d ", a[j]);
    }
    printf("\n");
    return 0;
}

现象：
这里写图片描述

六.堆排序

思想：根据堆的特性（堆中某个节点的值总是不大于或不小于其父节点的值，堆顶一定是最大或者最小值），每次将堆顶的最大值或最小值取出，然后再建新堆，再找出，再建。。。
以下为大顶堆的例子：
现在我们有一个完全二叉树：左子树和右子树都符合最大堆–>父>子
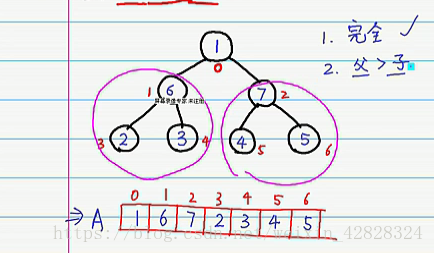
这里写图片描述
但是我们会发现：根元素所在的数并不符合，明显的是：1是小于7的
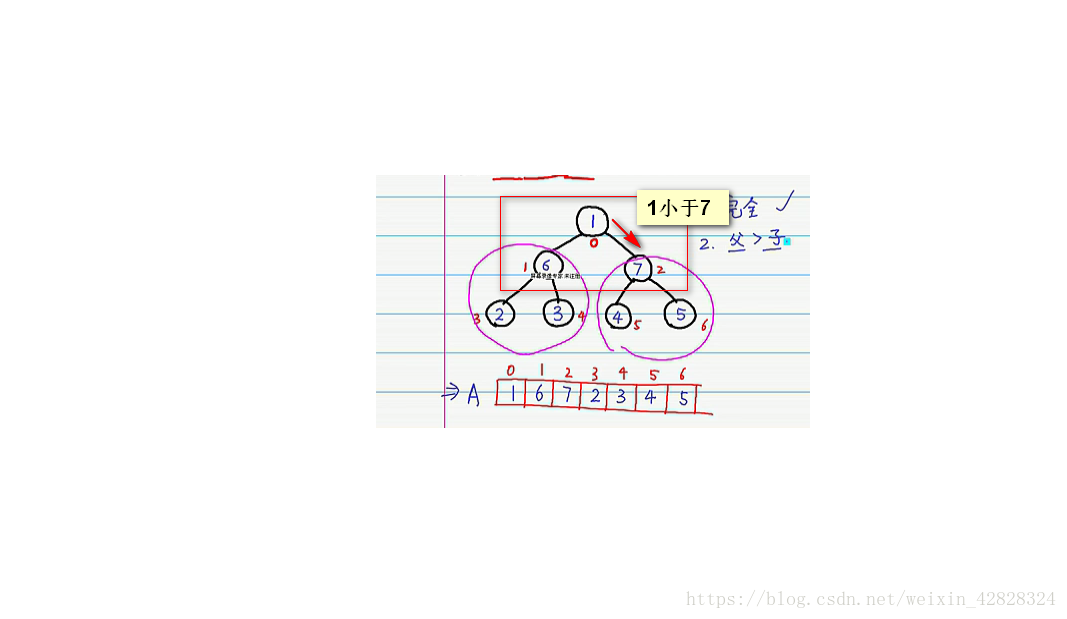
这里写图片描述
我们就对其进行交换，交换完之后我们会发现：右子树又不符合了～
因为，右子树变成了这样：
这里写图片描述
最后，我们将右子数的最大值也交换到右子树的根元素上
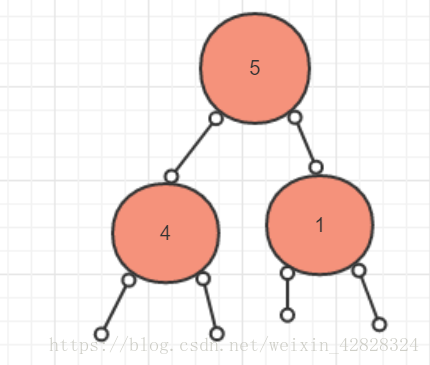
这里写图片描述
于是我们第一次的建堆操作就完成了！
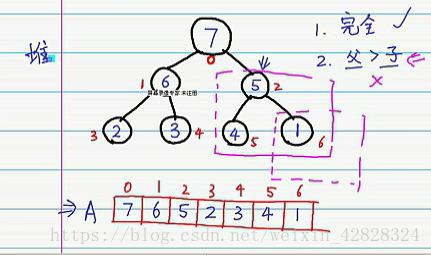
这里写图片描述
可以发现的是：一次堆建立完之后，我们的最大值就在了堆的根节点上
随后将堆顶最大值和数组最后的元素进行替换，我们就完成了一趟排序了。
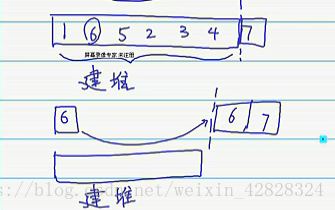
这里写图片描述
接下来，剩下的数不断进行建堆，交换就可以完成我们的堆排序了
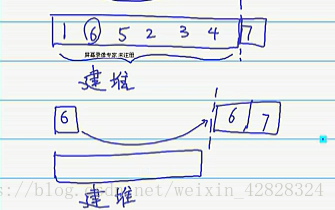
这里写图片描述
………建堆，交换….建堆，交换…建堆，交换…建堆，交换..
代码：
以下为小顶堆代码

#include<stdio.h>
void Swap(int* a,int* b) 
{
    int temp=*a;
    *a=*b;
    *b=temp;
}
void PercDown(int  A[], int i, int N) 
{
    int child;
    int Tmp;
    for (Tmp = A[i]; 2*i+1 < N; i = child) 
    {
        child = 2*i+1;
        //注意数组下标是从0开始的，所以左孩子不是2*i
        if (child != N - 1 && A[child + 1] > A[child])
                            ++child;
        //找到最大的子节点
        if (Tmp < A[child])
                            A[i] = A[child]; else
                            break;
    }
    A[i] = Tmp;
}
void HeapSort(int A[], int N) 
{
    int i;
    for (i = N / 2; i >= 0; --i)
                PercDown(A, i, N);
    //构造堆
    for (i=N-1;i>0;--i) 
    {
        Swap(&A[0],&A[i]);
        //将最大元素（根）与数组末尾元素交换，从而删除最大元素，重新构造堆
        PercDown(A, 0, i);
    }
}
void Print(int A[],int N) 
{
    int i;
    for (i=0;i<N;i++) 
    {
        printf(" %d ",A[i]);
    }
}
int main() 
{
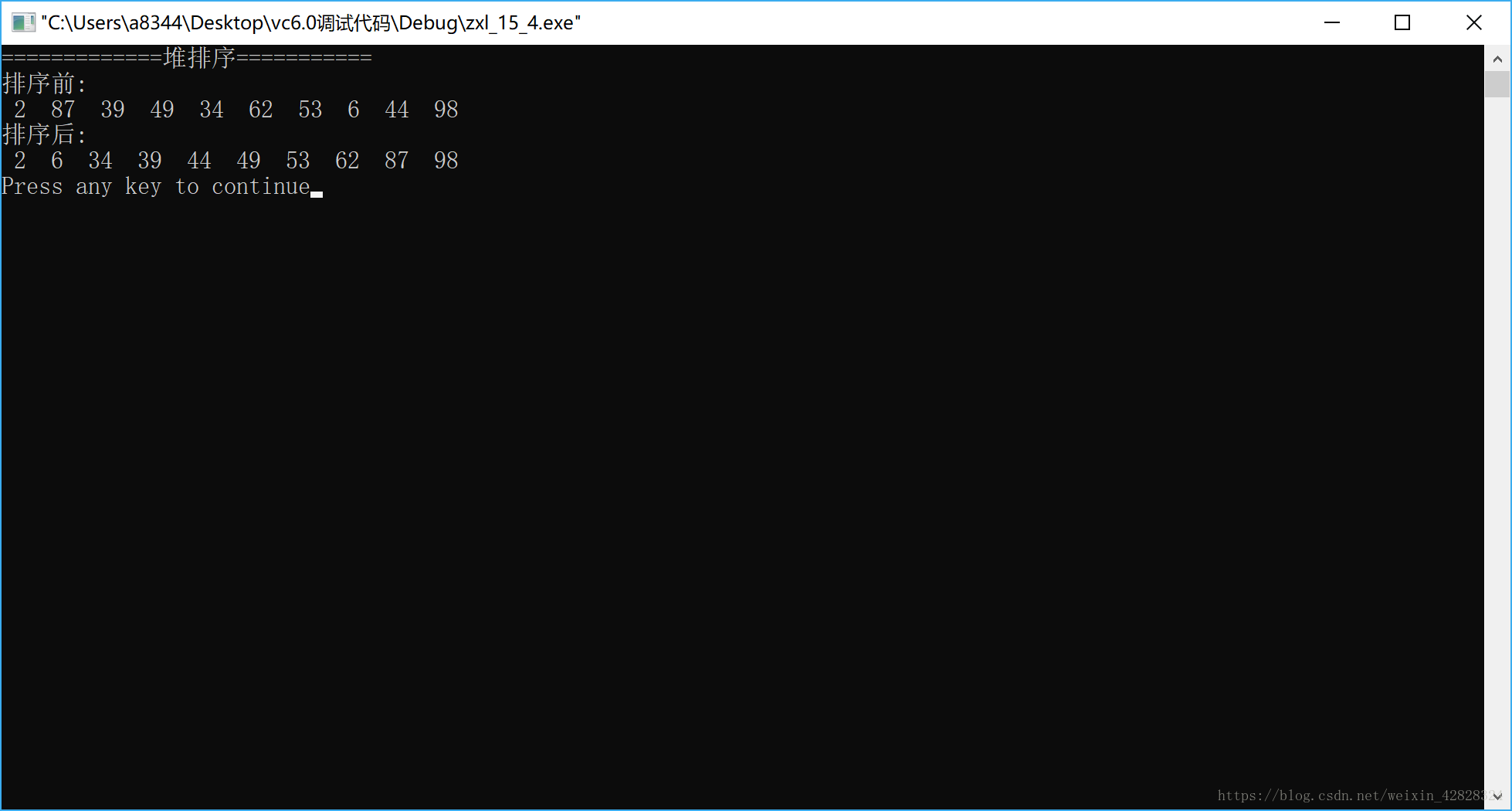
    int arr[10]={2,87,39,49,34,62,53,6,44,98};
    printf("=============堆排序===========\n");
    printf("排序前:\n");
    Print(arr,10);
    printf("\n");
    HeapSort(arr,10);
    printf("排序后:\n");
    Print(arr,10);
    printf("\n");
    return 0;
}

现象：
这里写图片描述

七.并归排序

思想：

申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
设定两个指针，最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
重复步骤3直到某一指针到达序列尾
将另一序列剩下的所有元素直接复制到合并序列尾

可能不太好理解，可以参考这个链接理解一下

代码：

#include<stdlib.h>   
#include<stdio.h>
typedef int RecType;
//要排序元素类型  
void Merge(RecType *R,int low,int m,int high) 
{
    //将两个有序的子文件R[low..m)和R[m+1..high]归并成一个有序的子文件R[low..high]  
    int i=low,j=m+1,p=0;
    //置初始值  
    RecType *R1;
    //R1是局部向量  
    R1=(RecType *)malloc((high-low+1)*sizeof(RecType));
    if(!R1) 
    {
        return;
        //申请空间失败
    }
    while(i<=m&&j<=high)                //两子文件非空时取其小者输出到R1[p]上 
    {
        R1[p++]=(R[i]<=R[j])?R[i++]:R[j++];
    }
    while(i<=m)                         //若第1个子文件非空，则复制剩余记录到R1中 
    {
        R1[p++]=R[i++];
    }
    while(j<=high)                      //若第2个子文件非空，则复制剩余记录到R1中 
    {
        R1[p++]=R[j++];
    }
    for (p=0,i=low;i<=high;p++,i++) 
    {
        R[i]=R1[p];
        //归并完成后将结果复制回R[low..high]
    }
}
void MergeSort(RecType R[],int low,int high) 
{
    //用分治法对R[low..high]进行二路归并排序  
    int mid;
    if(low<high) 
    {
        //区间长度大于1   
        mid=(low+high)/2;
        //分解  
        MergeSort(R,low,mid);
        //递归地对R[low..mid]排序  
        MergeSort(R,mid+1,high);
        //递归地对R[mid+1..high]排序  
        Merge(R,low,mid,high);
        //组合，将两个有序区归并为一个有序区
    }
}
void main() 
{
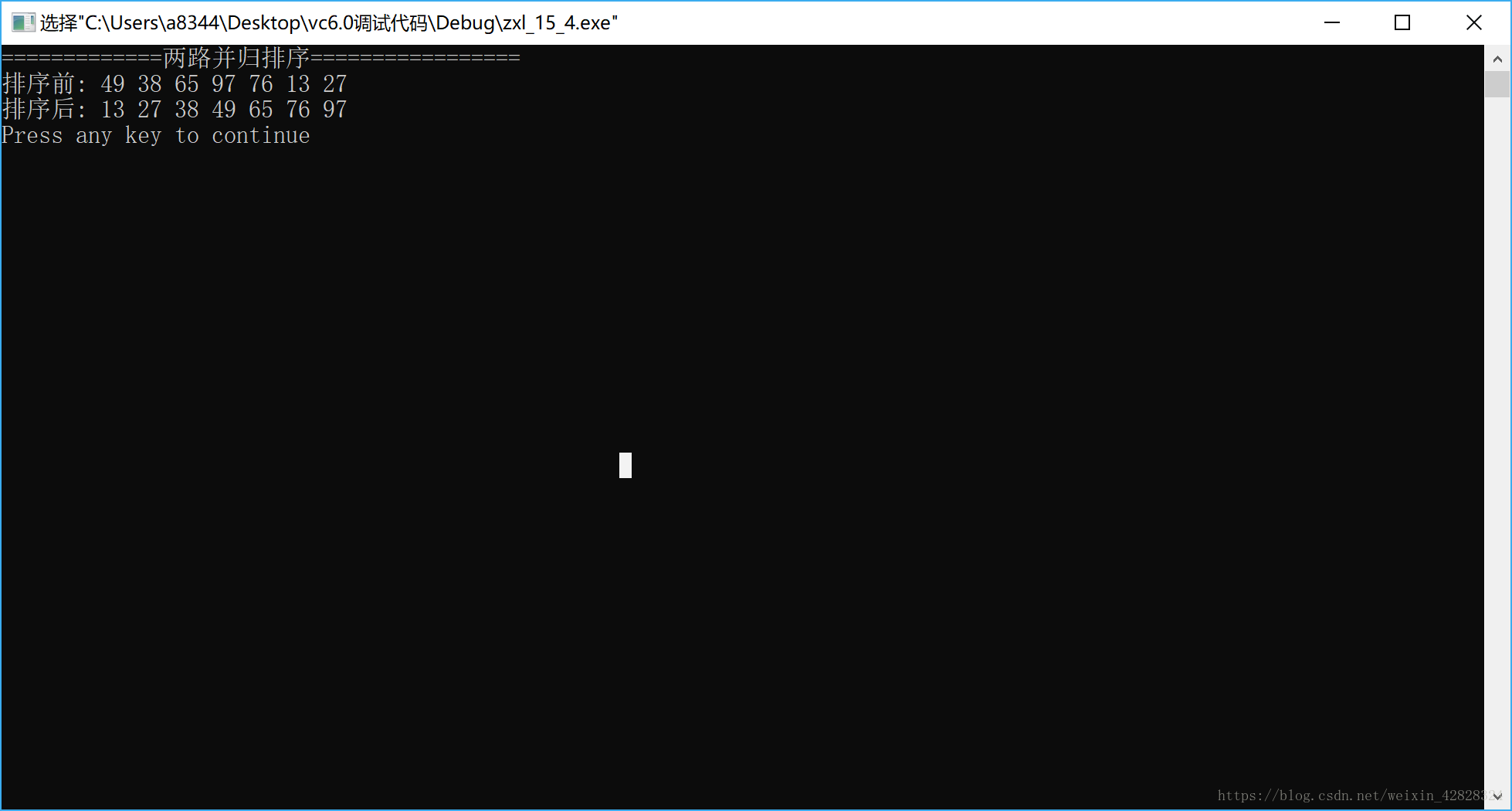
    int a[7]={49,38,65,97,76,13,27};
    //这里对8个元素进行排序  
    int low=0,high=6;
    //初始化low和high的值  
    int i;
    printf("=============两路并归排序=================\n");
    printf("排序前: ");
    for (i=low;i<=high;i++) 
    {
        printf("%d ",a[i]);
        //输出测试
    }
    printf("\n");
    MergeSort(a,low,high);
    printf("排序后: ");
    for ( i=low;i<=high;i++) 
    {
        printf("%d ",a[i]);
        //输出测试
    }
    printf("\n");
}

现象：
这里写图片描述

八.基数排序

基数排序是桶排序的扩展，先了解下桶排序。

思想：桶排序个人理解类似哈希表。将排序的数据放到桶里，初始时设置桶的数量，即排序的范围，如若要对100范围内的某10个数排序，即设置桶的数量为100，然后分别编号1到100，将要排序的10个数，放到与桶编号匹配的桶中。并将该编号的桶设置一个标志位，标志桶内有数据，输出时只要遍历所有桶，选择有数据的桶，并按编号输出即可。

代码：

#include <stdio.h>
#include <string.h>
#define MAX 100
void bucketsort(int A[],int size,int max_num)//size表示排序数组大小，max_num表示排序数组中最大的数 
{
    int i,j;
    int count[MAX];
    memset(count,0,sizeof(count));
    for ( i=0;i<size;i++) 
    {
        ++count[A[i]];
    }
    for (j=0;j<=max_num;j++) 
    {
        while(count[j]>0) 
        {
            printf("%d ",j);
            count[j]--;
        }
    }
    printf("\n");
}
int main() 
{
    int i;
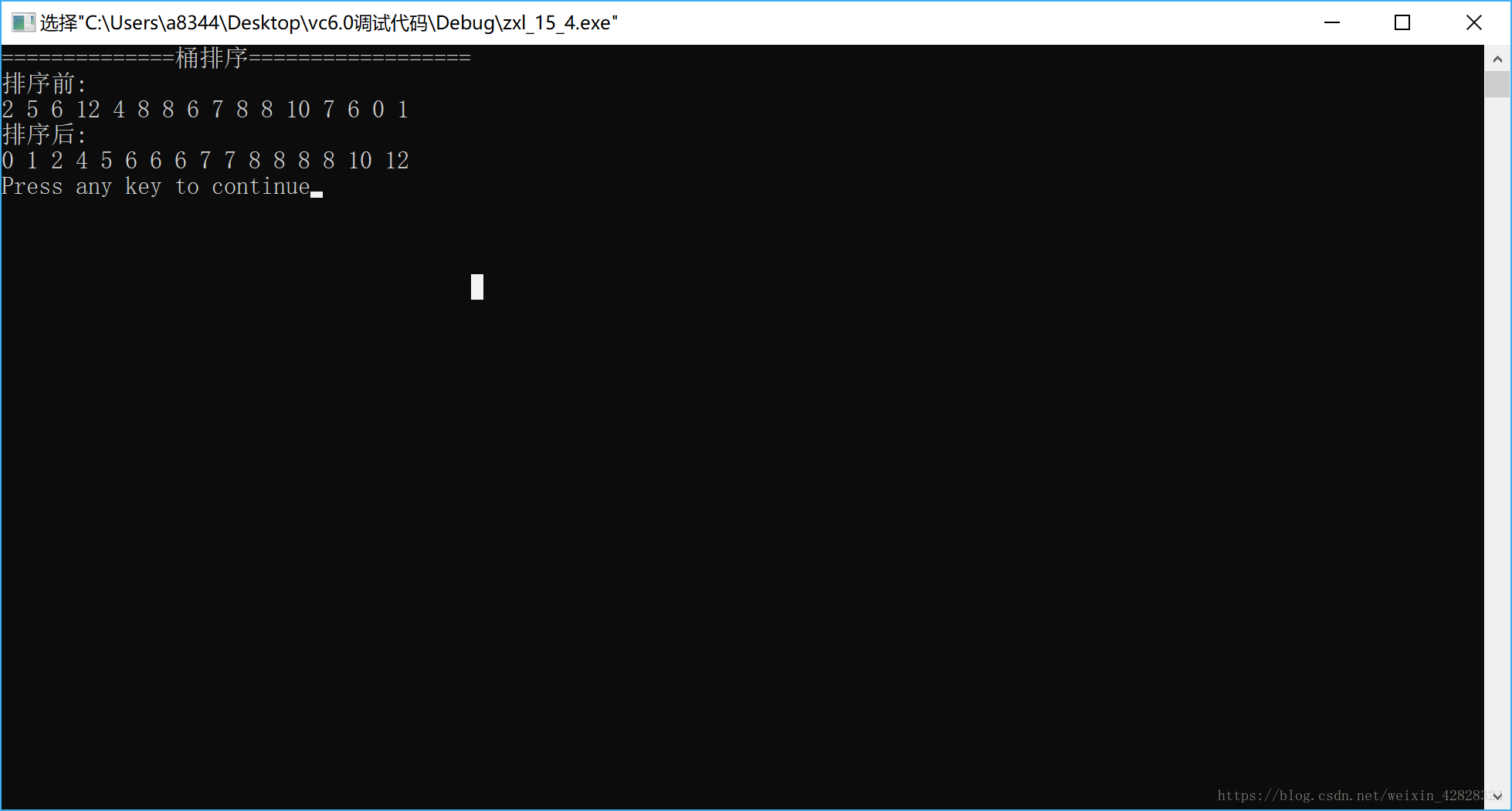
    int a[] = {2, 5, 6, 12, 4, 8, 8, 6, 7, 8, 8, 10, 7, 6, 0, 1};
    printf("==============桶排序==================\n");
    printf("排序前:\n");
    for (i=0;i<sizeof(a) / sizeof(a[0]);i++)
            printf("%d ",a[i]);
    printf("\n");
    printf("排序后:\n");
    bucketsort(a, sizeof(a) / sizeof(a[0]), 12);
    return 0;
}

现象：
这里写图片描述
基数排序：
思想：这里写图片描述
代码：

//Radix_Sort
#include <stdlib.h> 
#include <stdio.h>
/*被排序元素的最大位数，4则意味着只能排序< 10000 的数*/
#define WIDTH 4 
#define MAXK 10  //位数划分基于的基数，10表示为10进制划分
void radixSort(int a[], int n) 
{
    int i;
    void innerCountingSort(int a[], int n, int d);
    //内部的计数排序声明
    for (i = 0; i < WIDTH; i++) 
    {
        innerCountingSort(a, n, i);
        //对于每个元素的每一位都调用一次内部计数排序
    }
}
void innerCountingSort(int a[], int n, int d) //根据第d位数对数组进行排序 
{
    int i, j,k[MAXK] = {0};
    //数组K用来统计某一个元素的个数，该元素是待排序数组中某一位的数值
    int *ip = (int *)malloc(n * sizeof(int));
    //用来存储待排序数组的元素的某一位的数值
    int *bp = (int *)malloc(n * sizeof(int));
    int getDValue(int value, int d);
    //获取待排序数组元素的第d位的数值
    for (i = 0; i < n; i++) 
    {
        ip[i] = getDValue(a[i], d);
        k[ip[i]]++;
    }
    for (j = 1; j < MAXK; j++) //统计小于等于j的元素个数 
    {
        k[j] = k[j] + k[j-1];
    }
    for (i = n - 1; i >= 0; i--)//按照第d位的大小，将数组元素放置到正确的位置 
    {
        bp[k[ip[i]] - 1] = a[i];
        k[ip[i]]--;
    }
    for (i = 0; i < n; i++) //将按某一位排过序后的数组复制给原数组 
    {
        a[i] = bp[i];
    }
    free(ip);
    free(bp);
}
/*
*获取一个数第d位数的值，位数索引从0开始
*/
int getDValue(int value, int d) 
{
    for (;d > 0 && value > 0; d--) 
    {
        value = value / MAXK;
    }
    return value % MAXK;
}
void main() 
{
    int i;
    int A[]={1003,2343,5612,2334};
    printf("==============基数排序================\n");
    printf("排序前:\n");
    for ( i=0;i<4;++i)
                printf("%d ",A[i]);
    printf("\n");
    radixSort(A,4);
    printf("排序后:\n");
    for ( i=0;i<4;++i)
                printf("%d ",A[i]);
    printf("\n");
}

现象：
这里写图片描述

八大排序算法（C语言实现）
qq_73874574的博客
05-19 820
由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存。快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。选取左边，中间，右边，既不是最大，也不是最小的那个数做key。
常见八大排序(纯C语言版)
ikuunnnn的博客
06-08 2018
关于基本排序的万字讲解大全图文齐全
八大排序算法C语言
04-19
总结了八大排序算法的写法，并且比较了效率，供大家学习借鉴。
八大排序算法(C语言)
xiupong的博客
08-27 173
冒泡排序 简单选择排序 直接插入排序 希尔排序 快速排序 归并排序 堆排序 基数排序 时间复杂度 空间复杂度 稳定性 选择 O(N*N) O(1) 无 冒泡 O(N*N) O(1) 有 插入 O(N*N) O(1) 有 归并 O(N*logN) O(N) 有 快排(随) O(N*logN) O(logN) 无 堆 O(N*logN) O(1) 无 1)基数比较 时间复杂度小于0(N*logN) ------>不行 2)时间复杂.
C语言实现八大排序算法
最新发布
weixin_73629886的博客
12-13 1599
插入排序->希尔排序、选择排序->堆排序、交换排序->冒泡排序->快速排序、归并排序
C语言实现八大排序算法合集
07-20
c语言
必须知道的C语言八大排序算法(收藏)
12-31
我们这里说说八大排序就是内部排序。  当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序序。  快速排序：是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是...
排序算法实战练习
uiop_uiop_uiop的博客
01-25 1321
排序总的来说可以分为两种： 内排序：排序过程全部在内存中进行。外排序：排序过程需要不断地进行内存和外存之间的数据交换。外部排序时，要将数据分批调入内存来排序，中间结果还要及时放入外存，显然外部排序要复杂得多。 下面主要实战练习内排序。 目录 直接插入排序 （二路）归并排序 希尔排序   快速排序 左右指针法 挖坑法 前后指针法 快速排序的优化 堆排序 冒泡排序 直...
8种排序算法-测评对比（c语言程序）
06-11
按严蔚敏《数据结构》教材中的数据结构，实现了多种排序算法的程序设计，并进行实际数据输入测试对比。
八大排序算法C/C++实现
09-11
八大排序算法C/C++实现
C语言的八大排序详细
01-17
八大排序的详解、代码、例题、图解，各种排序的算法比较和用法。
C语言编程八大排序汇总
05-07
C语言编程八大排序汇总
C语言八大排序算法，一文带你弄清所有
qq_43813140的博客
05-20 2054
C语言八大排序 前言：感谢各位老前辈的写的算法解析，下面的图解也是由网上很多老前辈的图，收下我的膝盖。 代码全部由我实测，全都是能用的，不存在不能用的。 写着这篇博客，一方面是自己搞懂八大排序的一个过程，也希望能够帮助到目前的你 如果有错，还请指正 1、插入排序 将第一个和第二个元素排好序，然后将第3个元素插入到已经排好序的元素中，依次类推（插入排序最好的情况就是数组已经有序了） #include <bits/stdc++.h> using...
十大排序算法基本原理及其实现
weixin_61543874的博客
07-09 1267
十大排序算法基本原理及其实现
C语言八大排序算法【详细 代码+图文】
qq_43579888的博客
11-22 9831
C语言八大排序算法 辅助方法代码 void ShowArr(int* arr, int len) //显示数组 { for (int i = 0; i < len; ++i) { printf("%d ", arr[i]); } printf("\n"); } bool IsSort(int* arr, int len) //判断数据是否有序，从小到大 { for (int i = 0; i < len - 1; ++i) { if (arr[i] > arr[
八大排序算法C语言实现
weixin_38988633的博客
04-22 1466
八大排序算法 1 插入排序 1.1 直接插入排序 基本原理： 将第n个数插入已经排序好的，长度为n-1的序列中。从n-1长度的序列中查找出待插入的元素应该插入的位置；给插入元素腾出空间。 操作方法： 从第2个数开始遍历到第n个数。插入第i个数时，先与第i-1个数进行比较。因为前i-1个数已经为有序序列，如果i-1号数数值小于第i号数，则仍然有序，无需操作。否则，先将第i号数暂存于A[0]出。然后从...
八大排序算法的实现--C语言
weixin_43554618的博客
04-16 325
八大排序算法的实现–C语言 1.插入排序 void InsertSort(int* arr, int size) { for (int i = 0; i < size - 1; i++) { int end = i; int tmp = arr[end + 1]; while (end >= 0) { if (arr[end] > tmp) { ...
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值