【2014.01】普林斯顿数学指南(第一卷) [英]Timothy Gowers编 齐民友译

转过头来，事实上，解决许多几何问题的好方法是"把它转换成代数"。

这种做法最著名的例子是使用笛卡儿坐标。

例如，如果想把一个圆对经过圆心的直线L作反射，再逆时针旋转40度，然后再对同一直线L反射一次。

这个问题的一种做法是把它可视化如下：

 

想象这个圆是用薄的木片做的。

不必对此直线反射，而可以(通过木片外的第3维)绕L旋转180度。

再把所得的结果翻一个面，其实，如果对木片的厚度忽略不计，翻面并不起作用。

现在如果从木片下方往上看，并且让它逆时针旋转40度，则从原来的位置看，木片是顺时针旋转了40度，现在再把木片翻回来，即绕L在第3维里再旋转180度，总的效果就是顺时针方向旋转40度。

 

不同的数学家利用上面这种论证方法的意愿与能力是大不相同的。

如果您还不能充分可视地看出上面这种论证肯定是对的，就会喜欢按照代数途径，即利用线性代数和矩阵理论的方法(详见(I.3 ~ 3.2))。

开始是把圆看成适合x² + y²≤ 1的数对(x, y)的集合。

那两个变换，即对通过圆心的直线L的反射，以及旋转40度都可以用2 x 2的矩阵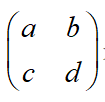来表示。

有一个稍微复杂一点的纯粹代数的法则把矩阵乘起来，而且这个法则就是这样来设计的，使之有这样的性质：如果矩阵A代表一个变换R(比如说是反射)，而矩阵B表示另一个变换T，则乘积AB就表示先作T再作R所得的变换。

因此我们可以这样来解决上面的问题：写出相应于这些变换的矩阵，把它们乘起来，再看是什么变换相应于这个乘积。

几何问题就这样转换成了一个代数问题，并且代数地解决。

 

    这样，尽管我们可以在几何与代数之间找出有用的区别，可是不要以为二者的界限是非常清晰的。

 事实上，数学的一个主要的分支就叫做代数几何[IV.4]。

 而上面的例子说明，时常可以把一点数学从代数变成儿何，反过来也一样。

 不论如何，在代数和几何的思维方式之间有确定的区别——一个比较注意符号，一个比较注意图像——这一点对于决定数学家追随哪个研究方向，有深刻的影响。