【读书2】【2014】基于MATLAB的雷达信号处理基础（第二版）——随角度变化的影响(2)

假设俯仰角ϕ是固定的，只考虑方位角θ的变化。

Suppose that theelevation angle ϕ is fixed, and consider only the variation in azimuth angle θ.

由于积分范围是一个完整的2π弧度，被积函数在θ上是以2π为周期的，方位角积分是周期函数的一个圆卷积。

Because theintegration is over a full 2π radians and the integrand is periodic in θ withperiod 2π, the integration over azimuth is a circular convolution of periodicfunctions.

如果θ是固定的，ϕ是变化的，因为被积函数仅在π弧度的范围内变化，则似乎不会出现这种情况。

This would not appearto be the case if instead θ is fixed and ϕ varies because the integrand is overa range of only π radians.

然而，也可以将式（2.119）有效地替换为

However, one couldequally well replace Eq. (2.119) as

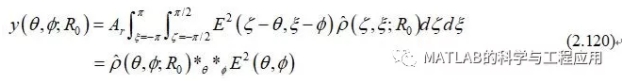
对于固定方位角，则在俯仰角上为周期函数的圆卷积。

For fixed azimuth,this is now a circular convolution of periodic functions in elevation.

总而言之，角变量上的两重积分在(θ, ϕ)空间上实现了二维加权平均。

Taken together, thetwo integrals over the angular variables implement a two-dimensional weightingand averaging over the (θ, ϕ) space.

只要天线波束宽度比2π小，该圆卷积将非常近似于(θ, ϕ)附近的线性卷积。

So long as theantenna beamwidths are small compared to 2π, this circular convolution willclosely approximate a linear convolution in the vicinity of (θ, ϕ).

图2.26直观地在一维角度上说明了式（2.119）所描述的过程。

Figure 2.26illustrates intuitively in one angle dimension the process described by Eq.(2.119).

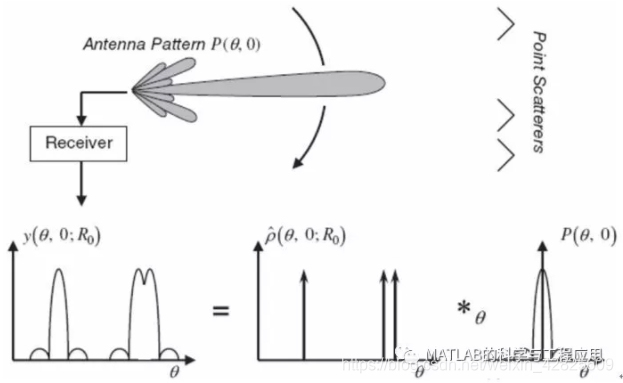
图2.26 当天线扫描经过点散射阵列时，接收机输出是天线方向图受点散射函数调制后的多重叠加When scanning past an array of point scatterers, the receiveroutput is a superposition of replicas of the antenna pattern.

——本文译自Mark A. Richards所著的《Fundamentals of Radar Signal Processing（Second edition）》

更多精彩文章请关注微信号：