判断一个数是否为4的幂

最新推荐文章于 2023-01-06 15:32:41 发布

原创最新推荐文章于 2023-01-06 15:32:41 发布 · 1k 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#2的幂 #4的幂

分析：

首先想到的肯定是for循环写出来，但是for循环写出来的肯定有大量的资源消耗，所以优化的话就是运用位运算来解决。

要想判断一个数是否为4的幂，先判断一个数是否为2的幂。

先看一下1到8 对应的二进制的数，能不能找到规律
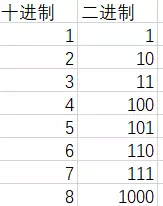
在这里插入图片描述

把2的幂单独摘出来，2的幂就是在上一个数的基础上乘2，而乘2在二进制中就是在后面补零。

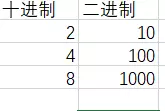
在这里插入图片描述

每个2的幂的数都是：首位为1后面都是0

那么怎么不用for循环判断呢？下面就是一个技巧：

在这里插入图片描述

2和1的二进制，进行&操作 ——> (10&1)==0

4和3的二进制，进行&操作 ——> (100&11)==0

8和7的二进制，进行&操作 ——> (1000&111)==0

这就是一个恒定的规律：如果(n&n-1)==0那么这个数一定是二的幂（限定：n-1>=0）。

接着那么怎么判断一个数是不是4的幂 ——> 找规律

把4的幂单独摘出来，4的幂就是在上一个数的基础上乘4，而乘4在二进制中就是在后面补两个零。
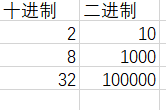
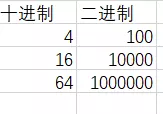
在这里插入图片描述

所以四进制的1一直都在奇数位上，那么找一个数进行&操作后，能判断出来1在奇数位还是在偶数位，那问题不就解决了。恰好，真有几个特殊的数

在这里插入图片描述
(n&0xaaaaaaaa)==0，那这个数不就是4的幂了，

(n&0x55555555）！=0，那这个数不就是4的幂了，

所以：

import java.util.Scanner;

public class exercise1 {

    public static void main(String[] args) {

        Scanner scan = new Scanner(System.in);

        long n = scan.nextLong();

        if((n&(n-1))==0&&n-1>=0&&(n&0x55555555)!=0) {

            System.out.println("true");

        }else {

            System.out.println("false");

        }

    }

}