Python数据分析---Numpy （3）_numpy 样本数据-优快云博客

本文详细介绍了使用NumPy进行数组操作的方法，包括数组的变形、组合与分割等常见操作，以及如何改编数组中的元素，例如插入、删除等，并提供了丰富的实例帮助理解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一.针对数组的操作

1.数组的变形
我们经常用 reshape ( )方法来变形数组
例如

   import   numpy   as   np
   np.arange( 10 )
   输出是0到9的一维数组
   
   np.arange( 10 ).reshape ( (2, 5 ) )
   输出为  array ( [ [0,1,2,3,4], [5,6,7,8,9] ] )
   这就将一维数组变成了二维数组
   尽管这两个数组的元素数量和内容一样，但两者不公用一个视图
   这里我们可以清楚看到参数里的2 就是数组的形状数
   当你需要转化回去时：
   np.arange (10).reshape( (10,) )

还有几种直接将多维数组转化成一维数组的方法

  b=np.array( [ [0,1,2,3,4], [5,6,7,8,9 ] ] )
  p=b.flatten( )
  p
  array([0,1,2,3,4,5,6,7,8,9 ] )
  flatten ( ) 方法       它与原数组不公用一个视图

以及
在这里插入图片描述
由此可以看出，通过ravel ( )方法获得的新数组与原数组公用一个视图，即改变其中部分，原数组跟着改变
既然有多维数组转化成一维数组的方法，当然也有一转多维的方法

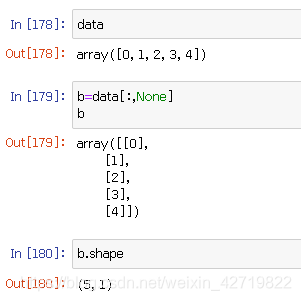
这是将一维数组转化成了二维数组

2.组合与分割
（1）水平组合
函数形式：np.hstack ( tup )，其中参数tup是一个元组,包含即将被组合在一起的数组
np.concatenate ( tup, axis=1 )也能实现
在这里插入图片描述
这其实是将两个数组水平拼接而成，相应的，也有垂直组合
（2）垂直组合
实现该功能的专有函数是 np.vstack ( )
但是此函数要求传入的数组在1轴方向上的形状相同

在这里插入图片描述

如上图，当1轴上的数值都是3时，才能用此方法，否则报错
而且，不难发现 b.T 其实就是将数组b旋转90度得到的

(3)数组的分割
这里用的时 split方法
在这里插入图片描述
这个方法传入三个参数，第一个是目标数组；第二个是分割成几部分；第三个参数，0代表水平分割，1代表竖直分割。
此外，针对每个方向的分割，也有专门的函数,如下

3.改编元素
用到的方法是np.append( )
这里有些不一样，也会有 "水平加” 和 “竖直加”
实验如下
在这里插入图片描述
如果指定 “水平加” ，那么就会和原来数组一致；如果不指定，默认合成的是一维数组。
注意：指定”竖直加 “会报错。

当然除了正常加入，还有插入，删除操作
我们来看一下
在这里插入图片描述

创建一个一维数组a1，插入操作用的是

insert 方法，注意，这里的 ‘1’ 是索引序号，即在第一个索引处添加数字100
delete方法，当指定 axis为0，删除的是水平分割后的第一个索引，留下的是第0个索引；当没有指定axis时，删除的时第一个索引值。
我们不难发现，这个所谓的删除，事实上是创建了一个不含指定元素的数组，对原来的数组没有丝毫的影响,即不公用一个视图