哈夫曼（huffman）树和哈夫曼编码

1、哈夫曼树
哈夫曼树是最优二叉树，树的结点度只有0和2，没有度为1的结点。n个叶子结点的哈夫曼树含有2*n-1个结点。
需要注意的点：
（1）满二叉树不一定是哈夫曼树；
（2）哈夫曼树中权越大的叶子结点距离根越近；
（3）具有相同带权结点的哈夫曼树不唯一；
（4）包含n棵树的森林要经过n-1次合并才能形成哈夫曼树，共产生n-1个新结点。
构造哈夫曼树：
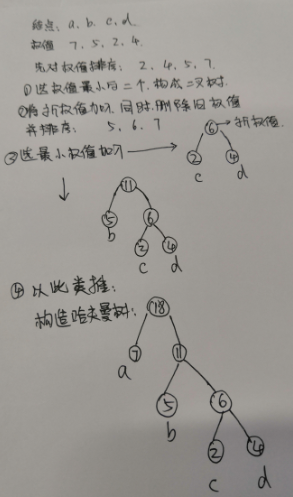
1.根据给定的n个权值{w1,w2,…,wn}构成二叉树集合F={T1,T2,…,Tn},其中每棵二叉树Ti中只有一个带权为wi的根结点,其左右子树为空.
2.在F中选取两棵根结点权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为左右子树根结点的权值之和.
3.在F中删除这两棵树,同时将新的二叉树加入F中.
4.重复2、3,直到F只含有一棵树为止.(得到哈夫曼树)
如： 有4 个结点 a, b, c, d，权值分别为 7, 5, 2, 4，构造哈夫曼树。

2、哈夫曼编码
必须保证译码的唯一性，任一字符的编码都不能是另一编码的前缀。
用二叉树设计二进制前缀编码
以电文中的字符作为叶子结点构造二叉树。然后将二叉树中结点引向 其左孩子的分支标 ‘0’，引向其右孩子的分支标 ‘1’； 每个字符的编码即为从根到每个叶子的路径上得到的 0, 1 序列。如此得到的即为二进制前缀编码。
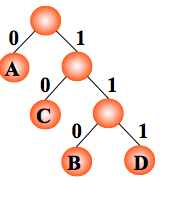电文译码的总长度：
权值为字符在电文中出现的次数 。