浮点数转字符字符串转换工具包-优快云博客

本文还有配套的精品资源，点击获取

简介：在嵌入式系统中，浮点数到字符字符串的转换是一项重要任务，主要应用于LCD或LED显示。这个过程涉及浮点数的存储和运算特点，特别是在资源有限的环境下，需要手动控制转换过程。本压缩包包含了浮点数到字符的转换程序或代码片段，以及相关的算法说明文档。它涵盖了浮点数的小数点位置和精度控制，以及特定硬件平台上可能遇到的浮点运算支持问题。通过使用本工具包，开发者可以更有效地处理显示数据的格式化问题，同时考虑到性能优化和硬件限制。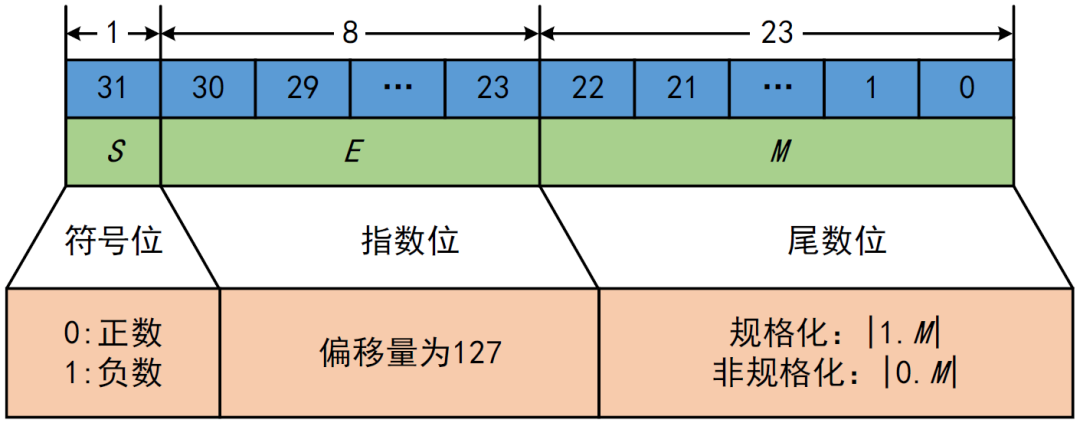

1. 浮点数的定义与IEEE 754标准

在现代计算机系统中，浮点数是表示实数的重要数据类型，尤其是当数值的范围和精度超出整数类型所能表达的范畴时。浮点数的表示方法虽然可以追溯到20世纪初期的科学计算，但直到1985年IEEE（电气和电子工程师协会）推出了IEEE 754标准，它才成为计算机界广泛接受的浮点数表示和运算规则。

1.1 浮点数的定义

浮点数由三部分组成：符号位、指数位和尾数位（也称为有效数字或分数位）。符号位决定了数值是正数还是负数，指数位用于确定数值的范围，尾数位则提供具体的精度。在实际应用中，浮点数可以表示非常大的数值，比如天文距离，也可以是极其微小的数值，比如物理常数。

1.2 IEEE 754标准

IEEE 754标准是一套国际公认的浮点数运算规则，它详细规定了浮点数的二进制表示方法、四则运算、舍入模式和异常处理等。该标准目前有两个广泛使用的版本：单精度（32位）和双精度（64位）。标准还定义了特殊的数值，比如正负无穷大和NaN（非数字），用于表示运算错误或其他特定情况。

1.2.1 IEEE 754标准的结构组成

IEEE 754格式中的单精度浮点数包含一个符号位、8位指数位和23位尾数位。双精度浮点数则有1位符号位、11位指数位和52位尾数位。这些不同的部分共同工作，允许计算机以一种标准化的方式处理浮点数的运算。

1.2.2 浮点数在标准下的表示方式

根据IEEE 754标准，浮点数的指数部分是偏移量编码（或称作指数偏移），它使得指数可以表示负数。以单精度为例，指数部分的偏移量是127。这样，如果指数字段是全零，则表示的实际指数是-127，用于表示非常接近零的数；如果指数字段是全1，则用于表示特殊数值，如无穷大或NaN。

通过理解这些基础定义和标准，我们能够更精确地处理和理解在计算过程中涉及浮点数的各种场景和问题。这不仅有助于编写更准确的数值计算程序，还可以更好地诊断和修复那些因浮点数表示不精确而导致的问题。

2. 浮点数转换为字符的理论基础

浮点数在计算机中是以特定的二进制格式存储的，而字符是在人类可以识别的文本形式中展示的。将浮点数转换为字符涉及到二进制到十进制的转换，以及格式化输出的处理。在本章节中，我们将深入探讨这一转换过程的原理，并对IEEE 754标准进行解析。

2.1 浮点数到字符字符串的转换原理

浮点数转换为字符涉及到了计算机科学中的一些核心概念，这包括数字的表示、二进制到十进制的转换，以及格式化输出的实现。

2.1.1 数据表示方法的演变

在计算机出现初期，整数的表示十分直接，直接使用二进制数即可。然而，随着科学计算的发展，人们需要一种方法来表示小数以及非常大或非常小的数值。这就是浮点数表示法的由来。早期的浮点数表示并不统一，不同的计算机系统可能会使用不同的浮点数表示方法。

2.1.2 转换过程中的精度问题

在将浮点数转换为字符的过程中，如何处理精度问题是一个重要的考量。由于浮点数通常是一个无限循环的小数，在转换为有限长度的字符时必然会导致精度损失。比如，浮点数表示中的尾数部分如果无限长，而字符表示只能精确到小数点后几位。这就要求在转换时进行合理的四舍五入处理，以确保输出结果既准确又符合使用场景的要求。

2.2 IEEE 754标准的深入解析

2.2.1 标准的结构组成

IEEE 754标准是国际上广泛认可的浮点数表示法。该标准定义了浮点数的存储格式、运算规则以及如何进行二进制到十进制的转换。一个标准的IEEE 754浮点数包括三个部分：符号位、指数位和尾数位。这种结构能够有效地表示范围广泛且精度各异的数值。

2.2.2 浮点数在标准下的表示方式

在IEEE 754标准中，一个32位的单精度浮点数包含1位符号位、8位指数位和23位尾数位。符号位表示数值的正负，指数位用于确定小数点的位置，尾数位则表示有效数字。对于双精度浮点数，则有1位符号位、11位指数位和52位尾数位，提供更高的精度。

让我们通过一个示例来更直观地理解这个过程：

#include <stdio.h>

int main() {
    float number = 12.3456789f;
    printf("%f\n", number);
    return 0;
}

在这个简单的例子中，我们定义了一个 float 类型的变量 number 并赋值为12.3456789，然后使用 printf 函数输出这个浮点数。当执行此代码时， printf 函数会自动调用浮点数到字符的转换机制，根据当前运行平台的IEEE 754标准将 number 的值转换为对应的字符表示。

12.345679

这是因为在IEEE 754标准下，float类型的浮点数在内存中占用32位，其中1位用来表示符号，8位表示指数，剩下的23位表示尾数。由于位数的限制，输出的字符字符串实际上是12.345679，而非完全的12.3456789，体现了在浮点数表示中的精度损失。

为了更好地理解这个转换过程，我们可以用以下表格来详细描述IEEE 754浮点数的构成要素。

| 成分 | 描述 | 位数 | |----------|------------------------------------------------------------|--------| | 符号位 | 表示数值的正负，0表示正数，1表示负数。 | 1位 | | 指数位 | 表示数值的大小，通过移码编码，将实际指数加上偏移量来表示。 | 8位 | | 尾数位 | 表示数值的有效数字部分，有时称为小数位。 | 23位 |

通过这样的表格，我们可以更清楚地看到IEEE 754浮点数各个组成部分的具体作用，以及它们在转换为字符形式输出时所起的关键作用。

在后续的章节中，我们将详细介绍嵌入式系统中浮点数显示的特殊要求，以及C/C++中浮点数格式化的实践应用，进一步探讨如何优化浮点数到字符的转换过程，以及如何在不同的硬件和软件环境中实现高效的浮点数处理。

3. 嵌入式系统中浮点数显示的特殊性

嵌入式系统由于其运行环境和硬件资源的特殊性，对浮点数的显示提出了不同于通用计算机系统的要求。本章节将深入探讨嵌入式系统中浮点数显示的特殊需求，以及在实际应用中如何应对这些挑战。

3.1 嵌入式系统对浮点数显示的特殊要求

3.1.1 硬件资源的限制

嵌入式设备通常受到存储空间、处理能力和功耗的严格限制。浮点数的存储和处理相比整数运算占用更多的资源。因此，在嵌入式系统中，浮点数的表示和显示必须优化以最小化资源的消耗。

硬件资源限制带来的挑战

存储空间限制导致需要高效的内存管理策略。
处理能力限制要求执行更少的浮点数运算，或使用更高效的算法。
功耗限制需要减少处理器的使用频率或在不影响性能的前提下降低电压。

3.1.2 显示精度与性能的平衡

在嵌入式系统中，通常需要在显示精度和系统性能之间做出平衡。高精度显示需要更多的计算资源，而低精度可能不足以满足应用的需求。

平衡显示精度与性能的策略

选择合适的浮点数表示方法，比如半精度浮点数(f16)，在满足精度要求的同时减少资源消耗。
在软件中实现动态精度调整，根据实际情况动态调整计算精度。
对于实时系统，采用预计算和查表法以避免复杂的浮点数运算。

3.2 嵌入式系统中浮点数显示的实践技巧

3.2.1 实时操作系统中的应用

在实时操作系统中，浮点数的显示和处理需要遵循实时性能的要求，以保证系统响应的及时性。

实时系统中的浮点数处理

使用固定点数代替浮点数，减少处理器开销。
在必要使用浮点数的情况下，尽量减少转换次数和优化算法。
使用DMA（直接内存访问）和中断驱动方法来处理浮点数的输入输出。

3.2.2 低功耗设备的优化方法

对于电池供电的低功耗设备，浮点数显示和处理的优化尤为重要，以延长电池寿命。

低功耗设备优化策略

实现节能的浮点数算法，如使用低能耗的数学函数。
利用低功耗模式，在不需要高精度显示时降低处理器频率。
采用多线程技术，合理分配CPU资源，避免不必要的浮点运算。

为了更好地展示嵌入式系统中浮点数显示的特殊性，下面是一个简单的表格，展示了在嵌入式系统中处理浮点数时可能采用的不同方法及其适用场景：

| 方法 | 适用场景 | |---------------------|-----------------------------------------| | 半精度浮点数(f16) | 显示精度要求不高，节约资源的应用 | | 动态精度调整 | 对精度和性能有动态要求的应用 | | 预计算和查表法 | 性能要求高，且计算模式可预测的应用 | | 固定点数代替 | 对浮点精度要求不高，节约资源的应用 | | DMA和中断驱动方法 | 实时系统中，减少处理器开销 | | 节能的浮点数算法 | 电池供电的设备，减少能耗 | | 多线程技术 | 合理分配资源，降低不必要的浮点运算开销 |

在嵌入式系统中，浮点数显示的优化和实现是一个复杂的过程，需要综合考虑硬件资源、功耗和实时性能等多种因素。通过以上技巧的合理应用，可以在满足应用需求的同时，最大限度地优化资源消耗。

4. C/C++中浮点数格式化的实践应用

4.1 C/C++中的标准浮点数格式化方法

4.1.1 `printf` 函数的使用与自定义格式

printf 函数是C/C++中常用的格式化输出函数，它允许程序员按照指定的格式输出数据。当涉及到浮点数时， printf 同样提供了一系列的格式化选项，其中最常用的是 %f 、 %e 和 %g 。

%f 用于以十进制形式输出浮点数，小数点后的位数可以通过 %.nf 指定。
%e 以科学计数法的形式输出，同样支持小数位数的指定。
%g 根据数值的大小自动在 %f 和 %e 之间选择较短的一种格式。

例如：

float num = 123.456f;
printf("Number = %f\n", num); // 输出: Number = 123.456002
printf("Number = %.2f\n", num); // 输出: Number = 123.46

4.1.2 `sprintf` 函数的使用与安全实践

sprintf 函数类似于 printf ，但是它将输出结果保存到字符串中而不是直接输出到标准输出设备。由于 sprintf 不直接显示结果，因此需要确保目标字符串有足够的空间来存储格式化后的数据。

这里有一个重要点： sprintf 容易引起缓冲区溢出，因为开发者有时会忽略对目标字符串大小的检查。因此，在使用 sprintf 时，推荐使用 snprintf ，后者允许你指定最大写入字符数，从而避免溢出：

char buffer[100];
float num = 123.456f;
snprintf(buffer, sizeof(buffer), "%.2f", num);

4.2 格式化输出的高级技巧与常见问题

4.2.1 精确度控制与四舍五入

精确度控制在金融和科学计算中尤为重要。 printf 的 %.*f 可以指定小数点后的精度，而 %.0f 可以实现四舍五入到整数。

double precise = 123.456789;
printf("Precision = %.3f\n", precise); // 输出: Precision = 123.457
printf("Rounded = %.0f\n", precise); // 输出: Rounded = 123

4.2.2 输出限制与异常处理

当浮点数的大小超出标准输出格式的范围时，会发生溢出。这通常在非常大或非常小的数值时发生。为了避免这种情况，可以使用 %g 或者自定义处理逻辑来根据数值的范围动态选择合适的格式。

异常处理还包括对NaN(非数字)和无穷大数值的处理。例如：

double nan = sqrt(-1);
double infinity = INFINITY;
printf("NaN = %f\n", nan); // 输出: NaN = -nan
printf("Infinity = %f\n", infinity); // 输出: Infinity = inf

对于上述情况，可能需要编写自定义代码来确保输出格式的正确性。此外，由于浮点运算的精度限制，可能需要编写额外的代码来校验结果的合理性。

5. 自定义浮点数到字符的转换算法

5.1 算法设计的理论基础

5.1.1 数学原理与算法结构

在自定义浮点数到字符的转换算法中，首先要理解基本的数学原理，因为这将构成算法的基础。浮点数通常由尾数（Mantissa）、基数（Base）、指数（Exponent）和符号位（Sign）组成。将浮点数转换为字符涉及以下步骤：

分离浮点数的各个组成部分。
将尾数部分转换成整数或者小数表示。
根据基数和指数调整尾数，确保转换后的数值准确无误。
根据符号位添加负号（如果数值为负）。
格式化最终的字符串，使其符合特定的输出要求。

算法结构上，我们通常采用以下模式进行实现：

输入：浮点数及其精度要求。
处理：将浮点数拆分、转换和调整。
输出：符合要求的字符串表示。

为了优化转换过程中的性能，算法往往采用舍入、缩放以及缓存等技术手段。

5.1.2 转换算法的性能评估

性能评估是设计转换算法不可忽视的一环。一个好的转换算法应当具备高效率、高准确性和良好的可扩展性。在性能评估时，我们通常关注以下指标：

转换速度：算法处理数据的能力，即单位时间内可以转换的浮点数的数量。
资源消耗：算法在内存和处理器上的消耗情况。
准确性：转换后字符的精确度与原始浮点数的对比。
可扩展性：算法是否能够处理不同精度和范围的浮点数。

通过对这些指标的测试和分析，我们可以不断优化算法，提高其在实际应用中的表现。

5.2 算法的实现与优化

5.2.1 编码实践与调试技巧

在实际编码实现中，我们首先需要选择合适的编程语言。通常，C或C++因其高效和接近硬件的特性成为这类任务的首选。以C语言为例，下面是一个简单的浮点数到字符串转换的函数实现。

#include <stdio.h>
#include <math.h>

// 将浮点数转换为字符串的示例函数
void float_to_string(double value, char* result, int precision) {
    // 使用sprintf函数进行基本转换
    sprintf(result, "%.*lf", precision, value);

    // 这里可以添加更多优化和错误处理逻辑
}

int main() {
    double value = 123.456789;
    char result[256];
    int precision = 6;
    float_to_string(value, result, precision);
    printf("Converted string: %s\n", result);
    return 0;
}

调试技巧主要围绕着理解各种边界条件、异常输入和数据类型限制。使用调试工具逐步执行代码，观察变量的变化，验证逻辑的正确性。对于浮点数转换，特别要注意浮点数在计算机内部的表示限制和舍入误差。

5.2.2 性能优化的方法与案例

在性能优化方面，关键在于减少不必要的计算和提高算法的效率。优化方法通常包括：

使用快速算法减少计算步骤，例如快速幂运算。
避免在循环中进行动态内存分配。
利用现代编译器的优化选项，如开启并行编译或向量化。

案例分析：针对上文中的转换函数，我们可以考虑以下优化措施：

#include <stdio.h>
#include <math.h>
#include <string.h>

// 优化后的浮点数到字符串转换函数
void optimized_float_to_string(double value, char* result, int precision) {
    // 使用快速幂和整数运算避免浮点运算
    // 以提高性能
    double temp = value;
    int exponent = 0;
    char buffer[512]; // 提前分配足够大的缓冲区以避免重分配
    // 此处省略了具体的快速幂算法实现和字符串构造过程...
    // 调整尾数以符合精度要求
    char* adjusted_result = buffer + strlen(buffer) - precision;
    sprintf(adjusted_result, "%.*lf", precision, temp);

    // 将结果复制到输出缓冲区
    memcpy(result, buffer, strlen(buffer) + 1);
}

int main() {
    double value = 123.456789;
    char result[512]; // 扩大缓冲区以适应优化后的算法
    int precision = 6;
    optimized_float_to_string(value, result, precision);
    printf("Optimized converted string: %s\n", result);
    return 0;
}

优化案例中，我们通过减少浮点运算，避免在处理过程中进行不必要的内存分配，同时将计算结果直接存储在预先分配的缓冲区内，以减少对 malloc 等调用的依赖，从而提升性能。优化后的算法，尤其在处理大量数据时，能够显著提高效率。

6. 硬件限制对浮点数格式化的影响

在现代计算系统中，硬件限制对浮点数格式化的影响是一个重要的考虑因素。浮点数的运算和表示方式在不同的硬件架构中可能有所不同，特别是对于CPU架构的差异性和浮点运算单元(FPU)的作用进行深入理解，对于开发高性能、高精度的应用程序至关重要。

6.1 硬件架构对浮点数处理的影响

硬件架构的设计直接影响着浮点数处理的效率和精度。现代CPU通过专门的浮点运算单元(FPU)来执行浮点数相关的运算任务，这些硬件设计上的差异性对于浮点数格式化的实现有着深远的影响。

6.1.1 CPU架构的差异性分析

CPU架构的不同设计选择，例如指令集、流水线深度、执行单元的宽度等，都会影响到浮点数的处理能力。例如，x86架构的CPU通常包含了成熟的x87 FPU指令集，而ARM架构的CPU则可能使用NEON指令集来处理浮点运算。这些差异意味着同样的浮点数格式化代码在不同的硬件架构上可能具有不同的性能表现。开发人员需要对目标硬件架构的特点有充分的理解，以便选择合适的算法和优化手段来提高程序的效率。

6.1.2 浮点运算单元(FPU)的作用

浮点运算单元(FPU)是CPU中的一个专门处理浮点数运算的硬件部分。FPU的效率和精度直接影响浮点数格式化的速度和结果的准确性。在不同架构中，FPU的设计也不尽相同。比如，某些FPU支持向量化的浮点运算，这可以显著提高并行处理能力，而有的FPU则可能更专注于单个浮点数的精确定义和运算。开发者需要考虑FPU的这些特性，并在程序设计中加以利用，以确保在特定硬件上获得最佳的性能表现。

6.2 硬件限制下的解决方案

了解了硬件架构对浮点数处理的影响后，我们可以探讨在硬件限制下，开发者应如何通过软件方法或者利用特定的硬件加速技术，来解决浮点数格式化过程中的性能和精度问题。

6.2.1 软件模拟方法

在没有专门的FPU或者FPU性能较差的硬件平台上，软件模拟浮点运算是一种可行的解决方案。这通常涉及使用整数运算来模拟浮点数的运算过程。虽然这种方法可能会显著降低运算速度，但可以通过算法优化来部分缓解性能损失。例如，采用查表法、基于二进制小数的运算技巧等技术，可以在没有硬件浮点单元的情况下，仍能有效地进行浮点数的格式化和运算处理。

6.2.2 硬件加速技术的应用

硬件加速技术，如使用GPU或专用的浮点运算芯片，可以大幅提高浮点运算的性能。例如，GPU中包含大量的并行处理单元，非常适合处理大规模并行的浮点数运算任务。针对特定的计算任务，比如图形渲染或者深度学习计算，使用专门设计的硬件加速器可以实现比传统CPU高几个数量级的性能提升。在软件层面，需要配合特定的编程接口和库，例如CUDA或OpenCL，以充分利用硬件加速技术的优势。

代码块示例与分析

考虑在ARM平台上实现一个浮点数到字符的转换函数，代码可能如下所示：

// 一个简单的浮点数到字符串的转换函数示例
char* float_to_string(float number) {
    static char buffer[32];
    sprintf(buffer, "%.6f", number);
    return buffer;
}

上述代码使用了 sprintf 函数来将浮点数转换为带有6位小数的字符串。在ARM这样的处理器上，由于其NEON指令集的高效性，这样的操作通常执行速度较快，但开发者应该关注浮点数的精度问题。

参数说明与执行逻辑

%.6f 指定了字符串的格式，即浮点数转换后的小数点后有六位数字。使用 sprintf 时，需要保证 buffer 的大小足够存放最终的字符串，以避免缓冲区溢出。

优化与扩展讨论

为了优化性能，可以考虑直接使用硬件加速的数学库，如ARM的NEON库，来实现浮点数到字符的转换。这通常涉及更底层的汇编指令操作，可以获得比标准库函数更高的性能，但也会牺牲一定的可移植性。

在第六章中，我们了解到硬件架构差异对浮点数格式化的深远影响，并探讨了解决方案，包括软件模拟和硬件加速技术的应用。通过合理的软件设计和硬件利用，可以在不同硬件平台上实现高效的浮点数处理，满足各种应用场景的精度和性能需求。

7. 浮点数显示的字符限制处理与平台支持问题

在浮点数的显示过程中，字符限制的处理和不同硬件平台的支持是确保数据准确性和可用性的重要方面。本章节将深入探讨这些方面的具体实践和解决方案。

7.1 字符限制的处理方法

当处理浮点数显示时，我们可能会遇到字符编码的限制，尤其是在资源受限的环境中。这通常发生在嵌入式系统或老旧的硬件平台上。处理这些问题的关键在于了解限制的来源并采取相应的策略。

7.1.1 字符编码的限制与解决方案

字符编码的限制通常来自于显示设备或终端对字符集的支持程度。例如，一些设备可能不支持Unicode字符集，或者显示空间有限，无法容纳长格式的浮点数字符串。

解决方案：

简化显示内容 ：对于不支持复杂字符集的设备，可以通过简化浮点数的显示内容，只保留用户关心的有效数字位数，来减少字符数。
自定义字符编码 ：如果标准字符集无法满足需求，可以考虑实现自定义的字符编码方案，以便更有效地利用显示资源。
使用缩写和符号 ：利用科学记数法或特定符号来代替长数字串，减少字符数同时保持信息的完整。

// 示例：使用科学记数法格式化浮点数输出
#include <stdio.h>

int main() {
    double number = ***.***;
    printf("%.3e\n", number); // 输出：1.234e+08
    return 0;
}

7.1.2 显示分辨率与用户界面优化

在拥有图形用户界面（GUI）的设备上，显示分辨率对浮点数的显示有很大影响。为了优化用户体验，需要考虑到浮点数的显示效果以及界面的整体美观。

解决方案：

动态调整显示格式 ：根据设备的屏幕大小和分辨率动态调整浮点数的显示格式，避免用户界面元素的挤压或拉伸。
增加用户自定义选项 ：允许用户根据个人喜好和需求调整浮点数的显示精度，比如设置小数点后的位数。
提供缩略图或缩放功能 ：在必要时，提供浮点数显示的缩略图，或者支持用户放大查看详细信息。

7.2 不同硬件平台上的浮点数支持

不同的硬件平台有着不同的浮点数处理能力和标准支持。了解这些差异性以及如何处理跨平台的浮点数支持，是实现应用兼容性的关键。

7.2.1 平台间兼容性分析

不同硬件平台可能使用不同的浮点数表示标准或指令集，比如IEEE 754标准在不同的处理器架构下可能会有不同的实现。

分析步骤：

检查浮点数支持 ：确定目标平台是否支持IEEE 754标准，以及支持的精度级别（单精度或双精度）。
检查指令集兼容性 ：了解平台是否支持常用的浮点运算指令集，如SSE或AVX。
软件模拟支持 ：如果目标平台不支持浮点数运算，考虑使用软件模拟方法。

7.2.2 跨平台浮点数处理的最佳实践

为了在不同的硬件平台上实现浮点数的正确和一致处理，采取一些最佳实践是必要的。

最佳实践：

使用浮点数库 ：使用可移植的浮点数库，如libm，确保在所有平台上具有一致的行为。
标准化测试 ：在不同平台上执行广泛的测试，确保浮点数的处理符合预期。
清晰的文档 ：记录浮点数处理的依赖和限制，并提供清晰的使用文档给最终用户。

// 示例：使用libm库的数学函数进行浮点数运算
#include <math.h>
#include <stdio.h>

int main() {
    double x = 1.0;
    double y = sqrt(x); // 使用libm的sqrt函数计算平方根
    printf("The square root of %.1f is %.1f\n", x, y);
    return 0;
}

这些方法和实践策略保证了浮点数显示在各种限制和平台上的适应性，不仅优化了用户体验，同时也保障了应用的功能性和稳定性。

本文还有配套的精品资源，点击获取