单循环链表结构详解与实现（带头结点与不带头结点）

本文还有配套的精品资源，点击获取

简介：单循环链表是一种重要的线性数据结构，通过节点间的指针连接形成一个闭环，适用于动态数据存储与处理场景。本文详细讲解了带头结点和不带头结点两种单循环链表的结构特点、操作实现及优缺点，并提供C++示例代码。通过学习，读者可以掌握链表的创建、插入、删除和遍历等核心操作，理解其在实际开发中的应用价值。

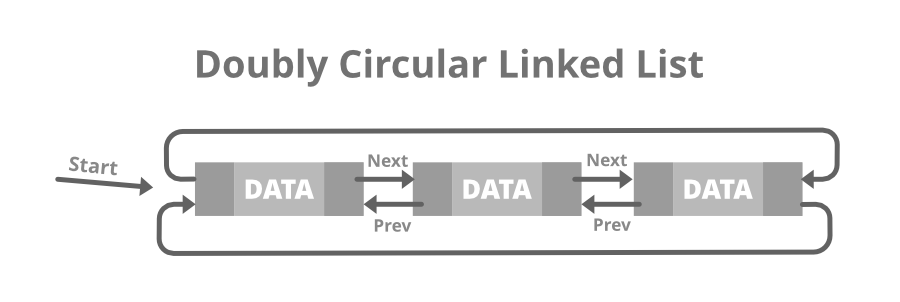
1. 单循环链表的基本概念与结构

单循环链表是一种特殊的链式数据结构，其核心特征在于 最后一个节点的指针不为空，而是指向头节点 ，从而形成一个闭环。这种结构继承了普通单链表的动态特性，同时通过“循环”机制增强了特定场景下的操作便利性。

从结构上看，单循环链表由多个节点组成，每个节点包含 数据域 和 指针域 。数据域用于存储数据元素，指针域则指向下一个节点。与普通链表不同的是，其尾节点不再指向 NULL，而是指向链表的头节点，形成一个环形结构。这种结构在实现如 循环队列、轮询调度 等场景中具有天然优势。

理解单循环链表的关键在于把握“循环”特性的实现机制，包括尾节点如何连接头节点、遍历时如何判断结束等。下一章将深入解析其结构特性与底层实现原理。

2. 单循环链表的结构特性与原理分析

单循环链表是一种特殊的链式数据结构，它通过在单链表的基础上将尾节点指向头节点，形成一个闭环。这种结构赋予了链表更强的遍历能力与灵活性，尤其适用于需要循环处理的场景。本章将深入探讨单循环链表的结构组成、工作原理、与数组的对比以及头结点与非头结点链表的结构差异，帮助读者建立对单循环链表的系统性理解。

2.1 单循环链表的基本结构

单循环链表的核心结构与普通单链表相似，但关键区别在于其最后一个节点的 next 指针不再指向 NULL ，而是指向链表的头节点，从而形成一个循环结构。

2.1.1 节点结构定义

一个基本的单循环链表节点通常由两部分组成：数据域和指针域。

typedef struct Node {
    int data;            // 数据域，存储节点的值
    struct Node* next;   // 指针域，指向下一个节点
} Node;

• data ：用于存储节点的值，可以是任意数据类型（本例中为 int ）。
• next ：指向下一个节点的指针。在单循环链表中，最后一个节点的 next 指向头节点，形成闭环。

⚠️ 注意：在初始化链表时，若链表为空，则头指针应指向 NULL 。当插入第一个节点时，该节点的 next 指针应指向自身，形成自循环。

2.1.2 指针的循环连接方式

单循环链表的循环特性通过指针连接实现。假设我们有如下节点结构：

Node* head = NULL;
Node* node1 = (Node*)malloc(sizeof(Node));
node1->data = 10;
node1->next = node1;  // 自循环
head = node1;

• 逻辑分析 ：
• node1->next = node1 表示当前节点的 next 指针指向自己。
• 这样，当链表只有一个节点时，仍然满足循环链表的定义。
• 后续添加节点时 ，需将新节点插入到链表中，并将最后一个节点的 next 指针重新指向头节点。

🧠 扩展思考：在实际开发中，为了简化插入和删除操作，通常会在链表头部引入一个“头结点”（dummy node），即使链表为空，头结点也始终存在。

2.2 单循环链表与数组的对比

单循环链表和数组是两种常见的线性结构，它们在存储方式、访问效率、插入删除操作等方面有显著差异。

2.2.1 存储方式与访问效率

特性	数组	单循环链表
存储方式	连续内存空间	非连续内存空间
访问效率	O(1)，支持随机访问	O(n)，必须顺序访问
插入/删除效率	O(n)，需移动元素	O(1)（已知插入位置）
空间灵活性	固定大小	动态扩展
循环访问能力	需手动控制	原生支持循环遍历

📈 图表说明：单循环链表虽然在访问效率上不如数组，但在动态插入和删除操作中表现更优，尤其是在需要频繁插入删除的场景下。

2.2.2 插入与删除操作的灵活性

• 数组插入/删除 ：
• 需要移动大量元素，时间复杂度为 O(n)。
• 无法动态扩展，除非使用动态数组（如 C++ 中的 vector ）。
• 链表插入/删除 ：
• 只需修改指针即可完成插入或删除。
• 在已知插入位置的情况下，时间复杂度为 O(1)。

// 插入节点示例：在 nodeA 后插入 nodeB
void insertAfter(Node* nodeA, Node* nodeB) {
    nodeB->next = nodeA->next;  // 新节点指向原节点的下一个节点
    nodeA->next = nodeB;        // 原节点指向新节点
}

• 逻辑分析 ：
• 第一行：将新节点 nodeB 的 next 指针指向 nodeA 的下一个节点。
• 第二行：将 nodeA 的 next 指针指向 nodeB 。
• 循环处理 ：
• 如果 nodeA 是尾节点，插入 nodeB 后，需将 nodeB 的 next 指针重新指向头节点以维持循环结构。

2.3 循环特性的工作原理

单循环链表的核心特性是“循环”，即最后一个节点指向头节点。这种结构使得链表可以无限遍历，适用于如任务调度、轮询机制等场景。

2.3.1 尾节点指向头节点的实现

构建单循环链表时，尾节点的 next 必须指向头节点。例如：

Node* createList(int n) {
    Node* head = (Node*)malloc(sizeof(Node));
    head->data = 1;
    head->next = NULL;

    Node* current = head;
    for (int i = 2; i <= n; ++i) {
        Node* newNode = (Node*)malloc(sizeof(Node));
        newNode->data = i;
        current->next = newNode;
        current = newNode;
    }
    current->next = head;  // 尾节点指向头节点，形成循环
    return head;
}

• 逻辑分析 ：
• current->next = head 是构建循环结构的关键步骤。
• 当 current 是最后一个节点时，将其 next 指向 head ，完成循环。
• 注意事项 ：
• 若链表为空（仅头结点），则 head->next = head ，实现自循环。

2.3.2 循环遍历的边界处理

由于链表是循环的，遍历时必须设置终止条件，否则会进入无限循环。

void traverse(Node* head) {
    if (head == NULL) return;
    Node* current = head;
    do {
        printf("%d -> ", current->data);
        current = current->next;
    } while (current != head);  // 终止条件：回到头节点
    printf("HEAD\n");
}

• 逻辑分析 ：
• 使用 do-while 循环确保至少执行一次打印。
• 终止条件为 current == head ，即回到起始节点。
• 优化建议 ：
• 可以使用计数器限制循环次数，防止链表结构异常导致死循环。

📊 mermaid 流程图：

graph TD
    A[开始遍历] --> B{链表是否为空?}
    B -- 是 --> C[返回]
    B -- 否 --> D[初始化 current 为 head]
    D --> E[打印 current 数据]
    E --> F[移动 current 到 next]
    F --> G{current == head?}
    G -- 否 --> E
    G -- 是 --> H[结束遍历]

2.4 头结点与非头结点链表的结构差异

在链表实现中，是否引入“头结点”对链表的逻辑统一性与操作简化有重要影响。

2.4.1 带头结点链表的逻辑统一性

带头结点的链表是指链表中始终存在一个不存储实际数据的节点，作为操作的统一入口。

typedef struct Node {
    int data;
    struct Node* next;
} Node;

Node* createDummyHeadedList() {
    Node* dummy = (Node*)malloc(sizeof(Node));
    dummy->next = dummy;  // 自循环
    return dummy;
}

• 优势 ：
• 插入、删除操作无需区分是否为头节点。
• 简化边界条件判断，提升代码可维护性。
• 逻辑分析 ：
• dummy->next = dummy 形成自循环，便于统一操作。
• 所有实际数据节点都插入在 dummy 之后，操作逻辑一致。

2.4.2 不带头结点链表的实现难点

不带头结点的链表中，头指针直接指向第一个数据节点，这在操作过程中需要额外判断头指针是否为空。

Node* head = NULL;

void insertAtHead(int value) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->data = value;
    if (head == NULL) {
        newNode->next = newNode;  // 自循环
        head = newNode;
    } else {
        newNode->next = head->next;
        head->next = newNode;
    }
}

• 逻辑分析 ：
• 判断 head == NULL 决定是否为首次插入。
• 若为首次插入，新节点形成自循环，并作为头节点。
• 否则，将新节点插入到头节点之后。
• 缺点 ：
• 插入、删除操作需频繁判断头指针状态。
• 边界条件处理复杂，容易引入逻辑错误。

对比维度	带头结点链表	不带头结点链表
插入操作	统一逻辑	需判断头节点是否存在
删除操作	无需特殊处理头节点	需处理头节点删除
实现复杂度	低	高
可读性与维护性	高	低

📌 结论：在实际开发中，推荐使用带头结点的单循环链表，以提高代码的健壮性和可维护性。

本章系统分析了单循环链表的基本结构、与数组的对比、循环特性的工作原理以及头结点与非头结点链表的结构差异。通过代码示例、流程图和对比表格，帮助读者深入理解其结构原理和实现方式，为后续的操作原理与算法分析打下坚实基础。

3. 单循环链表的操作原理与算法分析

在掌握了单循环链表的结构特性和基本概念后，接下来我们将深入探讨其核心操作的实现原理与算法逻辑。本章内容将围绕插入、删除、遍历等常见操作展开，详细分析其在单循环链表中的具体实现方式，以及如何通过头结点简化边界条件处理。通过对操作流程的逐步剖析，帮助读者理解单循环链表在实际开发中的使用方式和优化策略。

3.1 插入操作的基本原理

插入操作是链表中最常见的操作之一，它涉及到节点的创建、指针的调整和链表结构的维护。在单循环链表中，插入操作需要特别注意尾节点指向头节点的循环特性，确保插入后的链表仍然保持完整的循环结构。

3.1.1 插入位置的判断与定位

在单循环链表中，插入操作可以分为以下几种情况：

插入类型	描述
头部插入	在链表头部插入新节点，即在头结点之后插入新节点（若无头结点则直接插入为新的头节点）
中间插入	在指定位置的节点前或节点后插入新节点
尾部插入	在链表的最后一个节点之后插入新节点，同时更新尾节点指向头节点

插入操作的关键在于定位插入位置。通常我们会使用一个游标指针从头节点出发，遍历链表直到找到目标位置。例如，在尾部插入时，我们需要遍历到当前尾节点（即头节点的前一个节点），然后将新节点插入其后。

3.1.2 插入过程中指针的调整

以头部插入为例，假设我们有一个带头结点的单循环链表，其结构如下图所示：

graph LR
    head((head)) --> node1((1))
    node1 --> node2((2))
    node2 --> node3((3))
    node3 --> head

现在我们想要在头部插入一个值为 0 的新节点。插入过程如下：

1. 创建新节点 newNode ，将其 next 指针指向 head->next 。
2. 更新 head->next 指针，使其指向 newNode 。

代码实现如下：

typedef struct Node {
    int data;
    struct Node* next;
} ListNode;

void insertAtHead(ListNode* head, int value) {
    ListNode* newNode = (ListNode*)malloc(sizeof(ListNode));
    if (!newNode) {
        printf("Memory allocation failed\n");
        return;
    }
    newNode->data = value;

    // 1. 新节点的next指向原头节点的下一个节点
    newNode->next = head->next;

    // 2. 更新头节点的next指向新节点
    head->next = newNode;
}

逐行分析：

• 第 5 行：动态分配新节点内存空间。
• 第 8 行：判断内存分配是否成功，若失败则返回错误提示。
• 第 9 行：为新节点赋值。
• 第 12 行：将新节点的 next 指针指向当前链表的第一个有效节点。
• 第 15 行：更新头节点的 next 指针，完成插入。

通过这种方式，我们可以在头部快速插入新节点，时间复杂度为 O(1)。

3.2 删除操作的基本原理

与插入操作类似，删除操作也涉及节点的查找和指针的调整。在单循环链表中，删除操作需要特别注意链表的循环特性，确保删除节点后链表仍然保持循环结构。

3.2.1 删除节点的查找与释放

删除节点的流程包括以下几个步骤：

1. 从头节点出发，使用两个指针（ prev 和 curr ）遍历链表。
2. 查找目标节点，若找到则执行删除操作。
3. 释放目标节点内存，更新指针关系。

例如，我们要删除值为 target 的节点：

void deleteNode(ListNode* head, int target) {
    if (head == NULL || head->next == head) {
        printf("List is empty or head only\n");
        return;
    }

    ListNode* prev = head;
    ListNode* curr = head->next;

    // 查找目标节点
    while (curr != head && curr->data != target) {
        prev = curr;
        curr = curr->next;
    }

    // 判断是否找到目标节点
    if (curr == head) {
        printf("Node not found\n");
        return;
    }

    // 删除节点
    prev->next = curr->next;
    free(curr);
}

逐行分析：

• 第 1 行：定义删除函数，传入头节点和目标值。
• 第 3-5 行：检查链表是否为空或仅有头节点。
• 第 8-9 行：初始化双指针 prev 和 curr 。
• 第 12-15 行：遍历链表查找目标节点， curr == head 表示未找到。
• 第 18-20 行：若未找到目标节点，输出提示。
• 第 23 行：将前驱节点的 next 指向目标节点的下一个节点。
• 第 24 行：释放目标节点内存，完成删除。

3.2.2 删除后链表循环结构的维护

在删除操作中，我们需要确保链表仍然保持循环特性。例如，当删除尾节点时，新的尾节点应重新指向头节点：

graph LR
    head((head)) --> node1((1))
    node1 --> node2((2))
    node2 --> head

此时 node2 是新的尾节点，应将其 next 指向 head 。代码中可通过如下方式判断并更新：

if (curr->next == head) {
    // 若删除的是尾节点，则prev变为新的尾节点
    prev->next = head;
}

这样可以确保链表结构始终完整，避免断链。

3.3 遍历与打印的实现逻辑

遍历是访问链表所有节点的基础操作，而打印则是将节点数据输出到控制台或日志文件。在单循环链表中，遍历的终止条件尤为重要，因为链表本身是循环的。

3.3.1 终止条件的设置与判断

遍历操作的典型实现如下：

void traverseList(ListNode* head) {
    if (head == NULL || head->next == head) {
        printf("List is empty\n");
        return;
    }

    ListNode* curr = head->next;

    do {
        printf("%d -> ", curr->data);
        curr = curr->next;
    } while (curr != head);

    printf(" (back to head)\n");
}

逐行分析：

• 第 1 行：定义遍历函数。
• 第 3-5 行：检查链表是否为空。
• 第 8 行：从头节点的下一个节点开始遍历。
• 第 11-14 行：使用 do-while 循环确保至少执行一次循环体，直到 curr 回到头节点为止。
• 第 16 行：输出循环结束标志。

使用 do-while 而不是 while 是为了避免头节点自身被跳过，确保所有有效节点都被访问。

3.3.2 遍历过程中指针的移动

在遍历过程中，指针的移动逻辑非常关键。每次循环中， curr 指针会指向下一个节点，直到回到头节点为止。如下图所示：

graph LR
    head((head)) --> node1((1))
    node1 --> node2((2))
    node2 --> node3((3))
    node3 --> head

遍历顺序为： head → 1 → 2 → 3 → head ，形成完整的循环路径。

3.4 头结点在插入与删除中的作用

头结点的存在可以极大简化链表操作的边界条件处理，使插入和删除操作更加统一和高效。

3.4.1 简化边界条件处理

在没有头结点的链表中，插入和删除操作需要分别处理头节点和非头节点的情况。例如，在插入操作中：

• 插入头节点：需要修改头指针。
• 插入中间或尾节点：只需修改局部指针。

而引入头结点后，所有插入操作都可以统一为“在某个节点之后插入”，无需额外判断是否为头节点。

3.4.2 统一操作流程

以插入操作为例，无论插入位置是头部、中间还是尾部，都可以使用相同的插入逻辑：

// 插入新节点到prev节点之后
newNode->next = prev->next;
prev->next = newNode;

这样可以减少代码冗余，提高可维护性。

此外，在删除操作中，头结点也起到了统一作用。例如，在查找目标节点时，头结点可以作为“哨兵”节点，避免空指针异常。

本章从插入、删除、遍历等基本操作入手，详细分析了单循环链表在这些操作中的具体实现逻辑和算法流程。通过对头结点作用的探讨，我们了解到其在简化边界条件处理和统一操作流程中的重要作用。下一章我们将进入代码实现阶段，结合具体编程语言（如 C/C++）实现这些操作，并展示完整的代码示例和调试技巧。

4. 单循环链表的代码实现与操作实践

在本章中，我们将深入探讨单循环链表的代码实现，涵盖从链表的初始化、插入、删除到遍历与打印等基本操作。我们将分别实现带 头结点 与 不带头结点 的单循环链表，通过代码与图示结合的方式，帮助读者理解不同结构下的操作逻辑和边界处理。所有操作将基于C语言进行讲解，代码中包含详细的注释与逻辑分析，帮助读者掌握其实现原理。

4.1 单循环链表的初始化实现

链表的初始化是构建其结构的第一步。根据是否引入 头结点 （dummy node），我们可以将链表分为两种结构：带 头结点 和 不带头结点 。本节将分别介绍这两种结构的初始化方式。

4.1.1 带头结点链表的初始化

带头结点的链表在操作时可以统一处理各种边界情况，例如空链表插入、删除等，因此在工程实践中被广泛使用。

代码实现：

#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    int data;
    struct Node* next;
} Node;

// 初始化带头结点的单循环链表
Node* init带头链表() {
    Node* head = (Node*)malloc(sizeof(Node));  // 创建头结点
    if (!head) {
        printf("内存分配失败\n");
        exit(1);
    }
    head->next = head;  // 头结点指向自己，形成循环
    return head;
}

逻辑分析：

• 第4行定义了节点结构体 Node ，包含数据域 data 和指针域 next 。
• 第8行函数 init带头链表() 返回指向头结点的指针。
• 第10行使用 malloc 分配内存空间给头结点。
• 第13行设置头结点的 next 指针指向自己，形成一个空的循环链表结构。

参数说明：

参数名	类型	含义
无参数	-	初始化操作无需参数

小结：

带头结点的初始化结构在后续操作中能统一处理各种插入、删除情况，特别适用于复杂逻辑的工程代码。

4.1.2 不带头结点链表的初始化

不带头结点的链表结构更节省内存空间，但在实际操作中需要处理更多边界条件。

代码实现：

// 初始化不带头结点的单循环链表
Node* init无头链表() {
    return NULL;  // 初始为空指针
}

逻辑分析：

• 由于不带头结点，链表的起始指针直接为 NULL ，表示空链表。
• 插入第一个节点时，需要单独处理其循环特性。

参数说明：

参数名	类型	含义
无参数	-	初始化操作无需参数

表格对比：

项目	带头结点链表	不带头结点链表
初始化结构	指向自身循环的头节点	初始为 NULL 指针
内存占用	多一个头节点空间	节省一个节点空间
操作复杂度	操作统一，边界处理简单	插入删除需要判断空链表情况

4.2 插入操作的代码实现

插入操作是链表中最常见的操作之一。我们分别讨论带 头结点 与 不带头结点 情况下的插入逻辑。

4.2.1 带头结点情况下的插入实现

插入逻辑流程图：

graph TD
    A[开始] --> B[定位插入位置]
    B --> C[创建新节点]
    C --> D[调整指针连接]
    D --> E[完成插入]

代码实现：

// 在带头结点链表的第pos位置插入值为value的节点
void insert带头链表(Node* head, int pos, int value) {
    Node* current = head;
    int i = 0;

    // 定位插入位置的前一个节点
    while (i < pos - 1 && current->next != head) {
        current = current->next;
        i++;
    }

    Node* newNode = (Node*)malloc(sizeof(Node));
    if (!newNode) {
        printf("内存分配失败\n");
        exit(1);
    }

    newNode->data = value;

    // 插入新节点
    newNode->next = current->next;
    current->next = newNode;
}

逻辑分析：

• 第8~12行：通过 while 循环找到插入位置的前一个节点。
• 第15~18行：创建新节点并赋值。
• 第21~22行：将新节点插入到链表中，保持循环结构。

参数说明：

参数名	类型	含义
head	Node*	链表的头节点指针
pos	int	插入位置（从1开始计数）
value	int	插入节点的值

4.2.2 不带头结点情况下的插入实现

代码实现：

// 在不带头结点链表的第pos位置插入值为value的节点
Node* insert无头链表(Node* head, int pos, int value) {
    if (pos == 1) {  // 插入到链表头部
        Node* newNode = (Node*)malloc(sizeof(Node));
        newNode->data = value;
        if (!head) {  // 空链表
            newNode->next = newNode;
        } else {
            newNode->next = head->next;
            head->next = newNode;
        }
        return newNode;
    }

    Node* current = head;
    int i = 1;
    while (i < pos - 1 && current->next != head) {
        current = current->next;
        i++;
    }

    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->data = value;
    newNode->next = current->next;
    current->next = newNode;

    return head;
}

逻辑分析：

• 第3~12行处理插入位置为1（即头节点）的情况。
• 若链表为空，则新节点自己指向自己形成循环。
• 第14~24行处理插入中间或尾部的情况，与带头结点方式类似。

4.3 删除操作的代码实现

删除操作是链表中较为复杂的操作之一，需要特别注意循环结构的维护。

4.3.1 带头结点情况下的删除实现

代码实现：

// 删除带头结点链表中值为value的第一个节点
void delete带头链表(Node* head, int value) {
    Node* prev = head;
    Node* current = head->next;

    while (current != head && current->data != value) {
        prev = current;
        current = current->next;
    }

    if (current == head) {
        printf("未找到要删除的节点\n");
        return;
    }

    prev->next = current->next;
    free(current);
}

逻辑分析：

• 第4~7行：从头结点的下一个节点开始查找目标节点。
• 第10~12行：若未找到目标节点，则输出提示。
• 第14~15行：将前一个节点的 next 指向目标节点的下一个节点，并释放目标节点内存。

参数说明：

参数名	类型	含义
head	Node*	链表的头节点指针
value	int	要删除节点的值

4.3.2 不带头结点情况下的删除实现

代码实现：

// 删除不带头结点链表中值为value的第一个节点
Node* delete无头链表(Node* head, int value) {
    if (!head) {
        printf("链表为空\n");
        return NULL;
    }

    Node* current = head;
    Node* prev = NULL;

    do {
        if (current->data == value) {
            if (current == current->next) {  // 只有一个节点
                free(current);
                return NULL;
            }
            if (prev) {
                prev->next = current->next;
            } else {
                // 删除的是头节点
                Node* temp = current;
                while (temp->next != head) {
                    temp = temp->next;
                }
                head = current->next;
                temp->next = head;
            }
            free(current);
            return head;
        }
        prev = current;
        current = current->next;
    } while (current != head);

    printf("未找到要删除的节点\n");
    return head;
}

逻辑分析：

• 第3~5行处理空链表情况。
• 使用 do...while 循环确保至少执行一次。
• 第11行判断是否为最后一个节点。
• 第17~24行处理删除头节点的情况，需要重新连接尾节点。

4.4 链表遍历与打印功能实现

遍历是访问链表每个节点的基础操作，而打印功能是调试链表结构的重要工具。

4.4.1 遍历函数的编写与调用

代码实现：

// 遍历带头结点链表并打印
void traverse带头链表(Node* head) {
    Node* current = head->next;
    while (current != head) {
        printf("%d -> ", current->data);
        current = current->next;
    }
    printf("HEAD\n");
}

逻辑分析：

• 从头结点的下一个节点开始遍历。
• 当 current == head 时，说明已回到起点，遍历结束。

参数说明：

参数名	类型	含义
head	Node*	链表的头节点指针

4.4.2 打印输出的格式设计与优化

为了增强可读性，我们可以在打印时使用更直观的格式。

优化打印代码：

void print带头链表(Node* head) {
    Node* current = head->next;
    printf("HEAD -> ");
    while (current != head) {
        printf("%d -> ", current->data);
        current = current->next;
    }
    printf("HEAD\n");
}

输出示例：

HEAD -> 10 -> 20 -> 30 -> HEAD

小结与后续

本章详细讲解了单循环链表的初始化、插入、删除以及遍历与打印功能的实现过程。通过代码与图示的结合，帮助读者理解了不同结构下的操作逻辑，特别是在带头结点与不带头结点之间的实现差异。

在下一章中，我们将进一步探讨单循环链表的实际应用场景、性能评估以及优化思路，帮助读者将其应用到真实项目中。

5. 单循环链表的应用场景与进阶思考

5.1 单循环链表的实际应用场景

5.1.1 缓存机制与循环队列实现

单循环链表的循环特性使其非常适合用于实现 循环队列 或 缓存淘汰策略 中的LRU（Least Recently Used）机制。在缓存系统中，当缓存容量达到上限时，需要将最久未使用的数据移除。通过单循环链表，可以将最近使用的节点移动到链表头部，从而在遍历时始终保留最近访问的数据。

以下是一个简单的循环缓存结构的伪代码示例：

typedef struct CacheNode {
    int key;
    int value;
    struct CacheNode *next;
} CacheNode;

// 查找并更新缓存
CacheNode* cache_get(CacheNode* head, int key) {
    CacheNode* current = head;
    CacheNode* prev = NULL;
    do {
        if (current->key == key) {
            // 将该节点移动到头部
            if (prev != NULL && current->next != head) {
                prev->next = current->next;
                current->next = head;
                head = current;
            }
            return current;
        }
        prev = current;
        current = current->next;
    } while (current != head);
    return NULL; // 未找到
}

代码说明：
- CacheNode 结构体表示缓存项。
- cache_get 函数在缓存中查找指定 key，若找到则将其移动到链表头部，体现最近使用。
- 使用 do-while 循环确保遍历整个循环链表。

5.1.2 游戏开发中的角色轮询机制

在游戏开发中，常需要实现 角色轮询 （如回合制游戏中的角色顺序执行）。例如，三个角色 A、B、C 按照顺序依次执行操作，使用单循环链表可以方便地实现这种轮询机制。

class PlayerNode:
    def __init__(self, name):
        self.name = name
        self.next = None

def create_player_list(names):
    head = PlayerNode(names[0])
    current = head
    for name in names[1:]:
        new_node = PlayerNode(name)
        current.next = new_node
        current = new_node
    current.next = head  # 构成循环
    return head

def next_player(current):
    return current.next

# 创建玩家循环链表
players = create_player_list(["A", "B", "C"])
current = players
for _ in range(6):  # 轮询6次
    print(f"当前角色：{current.name}")
    current = next_player(current)

输出示例：

当前角色：A
当前角色：B
当前角色：C
当前角色：A
当前角色：B
当前角色：C

代码说明：
- PlayerNode 类用于表示游戏角色节点。
- create_player_list 函数创建一个单循环链表，角色按顺序连接。
- next_player 函数返回下一个角色，实现轮询机制。

5.2 单循环链表的性能评估

5.2.1 时间复杂度与空间复杂度分析

操作类型	时间复杂度	空间复杂度	说明
插入（已知位置）	O(1)	O(1)	只需调整指针
删除（已知节点）	O(1)	O(1)	只需调整前后指针
查找	O(n)	O(1)	需要遍历链表
遍历	O(n)	O(1)	遍历整个链表一次

性能分析：
- 插入和删除操作的时间复杂度较低，但前提是已经定位到插入或删除位置。
- 查找操作的时间复杂度为 O(n)，不如数组的 O(1) 快速访问。
- 空间复杂度恒为 O(1)，仅用于指针操作，不涉及额外存储。

5.2.2 插入删除效率与数组对比

操作	单循环链表	数组
插入头部	O(1)	O(n)
插入尾部	O(1)（维护尾指针）	O(1)
插入中间	O(n)（查找） + O(1)	O(n)（复制）
删除头部	O(1)	O(n)
删除尾部	O(n)（无尾指针）	O(1)
删除中间	O(n)（查找） + O(1)	O(n)（复制）

分析结论：
- 单循环链表在插入和删除头部时效率显著优于数组。
- 数组在尾部操作和访问效率上更优，但插入中间或头部时需要移动大量元素。
- 单循环链表适合频繁插入删除、不常随机访问的场景。

5.3 单循环链表的扩展与优化思路

5.3.1 支持双向循环的链表结构

在某些应用场景中，如需 双向遍历 ，可以将单循环链表扩展为 双向循环链表 。每个节点不仅保存下一个节点的地址，还保存前一个节点的地址，形成双向循环结构。

typedef struct DoublyNode {
    int data;
    struct DoublyNode *prev;
    struct DoublyNode *next;
} DoublyNode;

// 初始化双向循环链表
DoublyNode* init_doubly_circular_list(int data) {
    DoublyNode* node = (DoublyNode*)malloc(sizeof(DoublyNode));
    node->data = data;
    node->prev = node;
    node->next = node;
    return node;
}

代码说明：
- DoublyNode 包含 prev 和 next 指针，支持双向遍历。
- 初始化时，节点的 prev 和 next 都指向自己，形成循环结构。
- 双向循环链表适用于需要频繁前后移动的场景，如浏览器的历史记录管理。

5.3.2 链表与哈希表的结合应用

为了提高查找效率，可以在链表结构中引入 哈希表 ，实现 O(1) 时间复杂度的查找操作。例如，在 LRU 缓存中，使用哈希表保存 key 到链表节点的映射。

class LRUCache:
    def __init__(self, capacity):
        self.capacity = capacity
        self.cache = {}  # key -> node
        self.head = None
        self.tail = None

    def get(self, key):
        if key in self.cache:
            node = self.cache[key]
            self._move_to_head(node)
            return node.value
        return -1

    def put(self, key, value):
        if key in self.cache:
            node = self.cache[key]
            node.value = value
            self._move_to_head(node)
        else:
            if len(self.cache) == self.capacity:
                self._remove_tail()
            new_node = Node(key, value)
            self.cache[key] = new_node
            self._add_to_head(new_node)

    # 辅助函数：移动节点到头部、删除尾节点等

说明：
- cache 字典用于 O(1) 时间查找节点。
- get 和 put 操作通过链表维护 LRU 顺序。
- 结合哈希表与链表，实现高效缓存管理。

5.4 从工程实践角度思考链表设计

5.4.1 代码可维护性与结构清晰性

良好的代码结构是工程实践中的关键。对于单循环链表，建议将操作封装为独立函数，如 insert_after 、 delete_node 、 traverse 等，以提高可读性和复用性。

// 插入节点的函数封装
void insert_after(Node* prev_node, int data) {
    Node* new_node = (Node*)malloc(sizeof(Node));
    new_node->data = data;
    new_node->next = prev_node->next;
    prev_node->next = new_node;
}

优点：
- 函数职责单一，便于调试和维护。
- 可在多个模块中复用，减少代码冗余。

5.4.2 头结点设计的利弊权衡

头结点（dummy node）在链表操作中起到简化边界条件的作用。例如，在插入或删除操作中，无需单独处理头节点的特殊情况。

Node* dummy = (Node*)malloc(sizeof(Node));
dummy->next = head;

Node* prev = dummy;
Node* current = head;
while (current != NULL) {
    if (current->data == target) {
        prev->next = current->next;
        free(current);
        break;
    }
    prev = current;
    current = current->next;
}
head = dummy->next;
free(dummy);

优点：
- 统一处理所有节点，避免头节点特殊判断。
- 提高代码健壮性，减少 bug。

缺点：
- 增加额外内存开销。
- 对新手而言理解成本略高。

（本章节内容到此结束）

本文还有配套的精品资源，点击获取

简介：单循环链表是一种重要的线性数据结构，通过节点间的指针连接形成一个闭环，适用于动态数据存储与处理场景。本文详细讲解了带头结点和不带头结点两种单循环链表的结构特点、操作实现及优缺点，并提供C++示例代码。通过学习，读者可以掌握链表的创建、插入、删除和遍历等核心操作，理解其在实际开发中的应用价值。

本文还有配套的精品资源，点击获取