一、单项选择题(共15题,每题2分,共计30分;每题有且仅有一个正确选项)
- 一个32位无符号整数可以表示的最大值,最接近下列哪个选项?( )
A. 4∗1094*10^94∗109
B. 3∗10103*10^{10}3∗1010
C. 2∗1092*10^92∗109
D. 2∗10102*10^{10}2∗1010
答案解析: A
32 位无符号整数最大值为232−1=42949672952^{32}-1=4294967295232−1=4294967295 ,最接近 4∗1094*10^94∗109。
- 在C++中,执行int x = 255; cout << (x & (x - 1));后,输出的结果是?( )
A. 255
B. 254
C. 128
D. 0
答案解析:B
255可以用28−12^8-128−1表示,他的8位补码=1111 1111,那么254就是1111 1110,按位与的结果最后一位变成0即254。
- 函数 calc(n) 的定义如下,则 calc(5) 的返回值是多少?( )
int calc(int n) {
if (n <= 1) return 1;
if (n % 2 == 0) return calc(n / 2) + 1;
else return calc(n - 1) + calc(n - 2);
}
A. 5
B. 6
C. 7
D. 8
答案解析:B
f(5)=f(4)+f(3)
简单打表👇
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| f(x) | 1 | 1 | ? | ? | ? | ? |
递归f(4)=f(2)+1
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| f(x) | 1 | 1 | ? | ? | ? | ? |
递归f(2)=f(1)+1, f(1)=1,所以f(2)=1+1=2
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| f(x) | 1 | 1 | 2 | ? | ? | ? |
回溯f(4)=f(2)+1=3
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| f(x) | 1 | 1 | 2 | ? | 3 | ? |
递归f(3)=f(2)+f(1)=2+1=3
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| f(x) | 1 | 1 | 2 | 3 | 3 | ? |
回溯f(5)=f(4)+f(3)=3+3=6
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| f(x) | 1 | 1 | 2 | 3 | 3 | 6 |
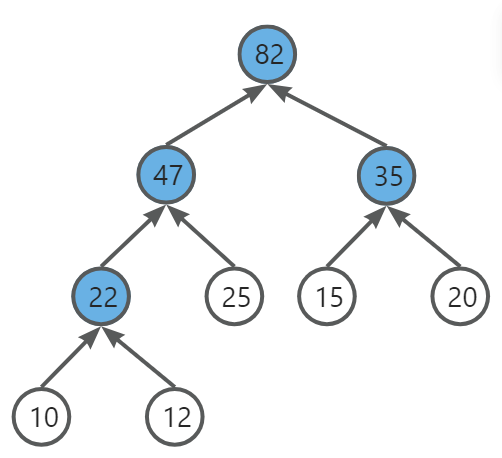
- 用5个权值10、12、15、20、25构造哈夫曼树,该树的带权路径长度是多少?( )
A. 176
B. 186
C. 196
D. 206
答案解析:B
带权路径长度是每个叶子节点的权值乘以其到根节点的路径长度,然后将所有叶子节点的这个乘积相加 ,又等于所有非叶子节点的权值之和。
10∗3+12∗3+25∗2+15∗2+20∗210*3+12*3+25*2+15*2+20*210∗3+12∗3+25∗2+15∗2+20∗2
=22+47+35+82=22+47+35+82=22+47+35+82
=186=186=186
- 在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和,这个总和等于?( )
A. 顶点数
B. 边数
C. 顶点数 + 边数
D. 顶点数 × 2
答案解析:B
根据握手定理,无向图中所有顶点的度数之和=边数的两倍, 有向图入度和 = 出度和 = 边数 。
- 从 5 位男生和 4 位女生中选出 4 人组成一个学习小组,要求学习小组中男生和女生都有。有多少种不同的选举方法?( )
A. 126
B. 121
C. 120
D. 100
答案解析:
C
减法:总选法-全男-全女
总选法=C94C_{9}^4C94 ,全男C54C_{5}^4C54 ,全女 C44C_{4}^4C44
答案=C94−C54−C44=126−5−1=120C_{9}^4-C_{5}^4-C_{4}^4=126-5-1=120C94−C54−C44=126−5−1=120。
加法:
1男3女+2男2女+3男1女
C51∗C43+C52∗C42+C53∗C41=20+10∗6+10∗4=120C_{5}^1*C_{4}^3+C_{5}^2*C_{4}^2+C_{5}^3*C_{4}^1=20+10*6+10*4=120C51∗C43+C52∗C42+C53∗C41=20+10∗6+10∗4=120。
- 假设a,b,c都是布尔变量,逻辑表达式(a && b) || (!c && a)的值与下列哪个表达式不始终相等? ( )
A. a && (b || !c)
B. (a || !c) && (b || !c)&&(a || a)
C. a && (!b || c)
D. !(!a || !b) || (a && !c)
答案解析:
C
(a && b) || (!c && a)可以写成a && (b || !c)
选项A:
完全一样。
选项 B:
(a||!c) && (b||!c) && (a||a)等价(a||!c) && (b||!c) && a
(a||a) 简化为 a(同一变量的逻辑或等价于自身)
a=1时(1||!c) && (b||!c) && 1
同1 && (b||!c) && 1
同(b||!c),跟题目结果一样
a=0时(0||!c) && (b||!c) && 0 = 0,跟题目结果一样。
选项C:
a && (!b || c)
a=0时答案同题目结果,a=1时中b和c的值会明显影响最终答案,所以选项C和题目不完全一样。
选项 D:
!(!a||!b) || (a&&!c)
a=1时!(0||!b) || (1&&!c)同!(!b) || !c = b || !c,跟题目结果一样
a=0时!(1||!b) || (0&&!c) = !(1) || 0 = 0,跟题目结果一样。
- 已知f[0] = 1, f[1] = 1,并且对于所有n≥2n \ge 2n≥2有f[n] = (f[n - 1] + f[n - 2]) % 7,那么 f[2025] 的值是多少? ( )
A. 2
B. 4
C. 5
D. 6
答案解析:D
发现十六个数字一周期,2025%16=9,f[9]=6。
- 下列关于C++ string类的说法,正确的是?( )
A. string 对象的长度在创建后不能改变。
B. 可以使用 + 运算符直接连接一个 string 对象和一个 char 类型的字符。
C. string 的 length() 和 size() 方法返回的值可能不同。
D. string 对象必须以 ‘\0’ 结尾,且这个结尾符计入 length()。
答案解析:B
string创建后长度可以修改
length() 和 size() 方法返回的值一样,不计\0。
- 考虑以下C++函数,在main函数调用solve后,x和y的值分别是?( )
void solve(int &a, int b) {
a = a + b;
b = a - b;
a = a - b;
}
int main() {
int x = 5, y = 10;
solve(x, y);
}
A. 5,10
B. 10,5
C. 10,10
D. 5,5
答案解析:
C
模拟即可 :a 传引用、b 传值。过程后 x=10,y 仍为 10。
- 一个8×8的棋盘,左上角坐标为 (1,1),右下角为 (8,8)。一个机器人从 (1,1)出发,每次只能向右或向下走一格。要到达 (4,5),有多少种不同的路径?( )
A. 20
B. 35
C. 56
D. 70
答案解析:B
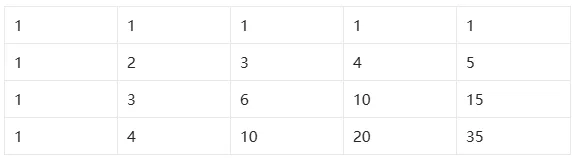
递推法:
排列组合:
共往右走4步,往下走3步,共7步, 每一步都可能往下或往右,所以7步里挑4个向右或7步里挑3个向下C73=C74=7∗6∗51∗2∗3=35C_{7}^3=C_{7}^4=\frac{7*6*5}{1*2*3}=35C73=C74=1∗2∗37∗6∗5=35。
- 某同学用冒泡排序对数组{6,1,5,2,4}\{6, 1, 5, 2,4\}{6,1,5,2,4}进行升序排序,请问需要进行多少次元素交换?( )
A. 5
B. 6
C. 7
D. 8
答案解析:B
模拟即可,或
冒泡交换次数 = 逆序数。序列 6 1 5 2 4 的逆序对数为 4+2=6。
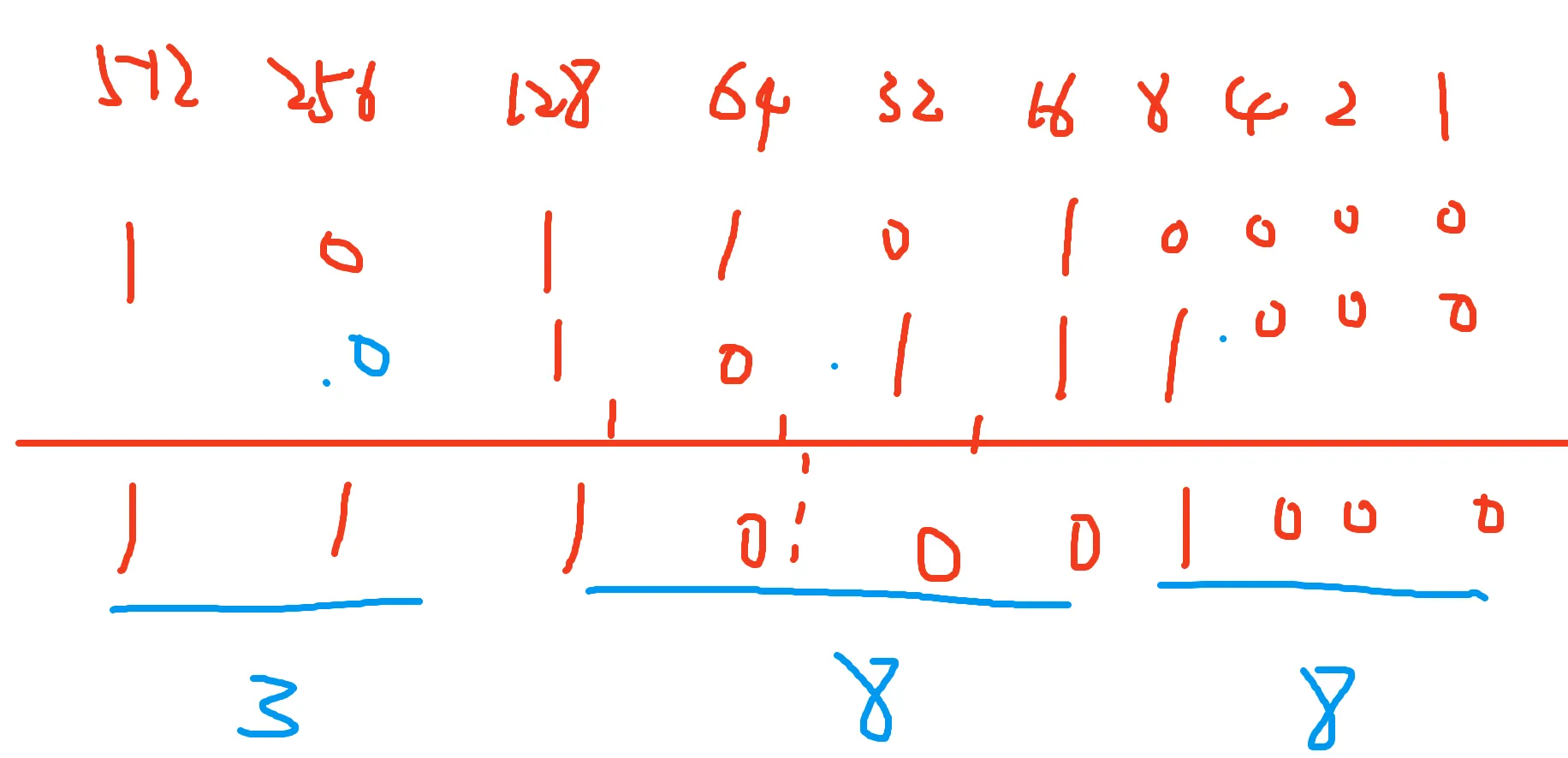
- 十进制数 72010720_1072010 和八进制数 2708270_82708 的和用十六进制表示是多少?( )
A. 38816
B. 3DE16
C. 28816
D. 99016
答案解析:A
方法不唯一,我喜欢10转2,8转2,相加,然后2转16。
- 一棵包含 1000 个结点的完全二叉树,其叶子结点的数量是多少?( )
A. 499
B. 512
C. 500
D. 501
答案解析:C
1000是最后一个节点,那么1000的父节点500是最后一个有子节点的节点,那么501~1000都是叶子,共500个,求父节点时向下取整,所以
完全二叉树叶子结点数=N−⌊N2⌋N-\lfloor \frac{N}{2} \rfloorN−⌊2N⌋===⌈N2⌉=⌈10002⌉=500\lceil \frac{N}{2} \rceil=\lceil \frac{1000}{2} \rceil=500⌈2N⌉=⌈21000⌉=500 。
- 给定一个初始为空的整数栈 S 和一个空的队列 P 。我们按顺序处理输入的整数队列 A:7,5,8,3,1, 4,2。对于队列 A 中的每一个数,执行以下规则:如果该数是奇数,则将其压入栈 S ;如果该数是偶数,且栈 S 非空,则弹出一个栈顶元素,并加入到队列P的末尾;如果该数是偶数,且栈S为空,则不进行任何操作。当队列 A 中的所有数都处理完毕后,队列 P 的内容是什么?( )
A. 5,1,3
B. 7,5,3
C. 3,1,5
D. 5,1,3,7
答案解析:A
模拟即可。
二、阅读程序(程序输入不超过数组或字符串定义的范围; 判断题正确填 ✓\checkmark✓,错误填×\times×;除特殊说明外,判断题1.5分, 选择题3分,共计40分)
(1)
#include <algorithm>
#include <cstdio>
#include <cstring>
inline int gcd(int a, int b) {
if (b == 0)
return a;
return gcd(b, a % b);
}
int main() {
int n;
scanf("%d", &n);
int ans = 0;
for (int i = 1; i <= n; ++i) {
for (int j = i + 1; j <= n; ++j) {
for (int k = j + 1; k <= n; ++k) {
if (gcd(i, j) == 1 && gcd(j, k) == 1 && gcd(i, k) == 1) {
++ans;
}
}
}
}
printf("%d\n", ans);
return 0;
}
判断题
- (1分)当输入为2时,程序并不会执行第 16 行的判断语句。( )
对
错
答案解析: ✓\checkmark✓
1<=i<j<k<=n,当n=2 时最内层 k 循环不进,判断语句不执行。
- 将第16行中的&& gcd(i, k)==1删去不会影响程序运行结果。( )
对
错
答案解析:X
程序计算的是1~n以内的三个数字两两互质,少写一个条件则增加满足条件的数字个数。
- 当输入的n≥3n \ge 3n≥3的时候,程序总是输出一个正整数。( )
对
错
答案解析: ✓\checkmark✓
当n=3时有1 2 3 三个数字两两互质,当n>3时答案不减。
单选题
4. 将第7行的gcd(b,a%b)改为gcd(a,a%b)后,程序可能出现的问题是( )。
A. 输出的答案大于原答案。
B. 输出的答案小于原答案。
C. 程序有可能陷入死循环。
D. 可能发生整型溢出问题。
答案解析:B
举例18%12==>18%6==>18%0,此时b为0输出a,则gcd(b,a%b)改为gcd(a,a%b)后输出a,但是gcd(j, k) == 1中j至少为2,所以条件永远为假,为1的情况=0。
- 当输入为8的时候,输出为( )。
A. 37
B. 42
C. 35
D. 25
答案解析:D
模拟即可:
当n=8时,三个8以内互素的数字组合有
1,2,【3,5,7】
1,3,【4,5,7,8】
1,4,【5,7】
1,5,【6,7,8】
1,6,【7】
1,7,【8】
2,3,【5,7】
2,5,【7】
3,4,【5,7】
3,5,【7,8】
3,7,8
4,5,7
5,6,7
5,7,8
共25个
- 调用gcd(36,42)会返回( )。
A. 6
B. 252
C. 3
D. 2
答案解析:A
欧几里得算法 36%42=42%36=36%6
(2)
#include <algorithm>
#include <cstdio>
#include <cstring>
#define ll long long
int n, k;
int a[200007];
int ans[200007];
int main() {
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
}
std::sort(a + 1, a + n + 1);
n = std::unique(a + 1, a + n + 1) - a - 1;
for (int i = 1, j = 0; i <= n; ++i) {
for (; j < i && a[i] - a[j + 1] > k; ++j)
;
ans[i] = ans[j] + 1;
}
printf("%d\n", ans[n]);
return 0;
}
判断题
- 当输入为“3 1 3 2 1”时,输出结果为2。( )
对
错
答案解析: ✓\checkmark✓
n=3,k=1,a[]={0,3,2,1},排序去重后a[]={0,1,2,3}
for (; j < i && a[i] - a[j + 1] > k; ++j);
i=1对第一个数来说是自己减自己,ans[1]=ans[0]+1=1
i=2对第二个数来说2-1也没有超过1,所以ans[2]=ans[0]+1=1
i=3对第三个数来说3-1超过了1,j++=1,3-2没有超过1,停止,ans[3]=ans[1]+1=2
所以该程序的主要功能是对输入的一组整数去重并排序后,划分成若干个区间,使得每个区间内最大值减最小值不超过 k,最后输出最少需要划分的区间数量
对于第一个数字来说为1个区间,自己和自己的距离是0
对于第二个数字来说,他和1的距离是1,没有超过1,所以也是一个区间
对于第三个数字来说,他不能和第一个数字合并,和第二个数字可以合并,所以总数量是2
ans[i] = ans[j] + 1表示前 i 个数最少需要划分的区间数量等于前 j 个数最少需要划分的区间数量加 1。
- 假设输入的n为正整数,输出的答案一定小于等于n,大于等于1。( )
对
错
答案解析: ✓\checkmark✓
最小一个区间,最大n个区间
- 将第14行的n = std::unique(a + 1, a + n + 1) - a - 1;删去后,有可能出现与原本代码不同的输出结果。 ( )
对
错
答案解析:X
unique 用于去重,删除去重部分,
当k为正数时,相同数字还是分在一个组,所以总组数不影响
讨论k为负的情况
模拟5个数1,2,2,2,2{1,2,2,2,2}1,2,2,2,2,k=-1
第一个数i=1,j=0,a[1]-a[1]=0,0大于-1,++j后j=1,不满足条件退循环,ans[1]=ans[1]+1=1
第二个数i=2,j=1,a[2]-a[2]=0,0大于-1,++j后j=2,不满足条件退循环,ans[2]=ans[2]+1=1
第三个数i=3,j=2,a[3]-a[3]=0,0大于-1,++j后j=3,不满足条件退循环,ans[3]=ans[3]+1=1
发现j会一直跟着i往后走到i,导致ans里的值一直是a[i]=a[i]+1=1,有没有可能j卡住不走然后再走呢?这样就可以i!=j,导致ans变大。
因为排好序了,所以a[i]减之前的数肯定>=0(因为没去重所以最小就是0),但是k为负数,所以a[i] - a[j + 1] > k一定满足,j一定会移动到i,所以答案不变为1
单选题
4. 假设输入的 a 数组和 k 均为正整数,执行第 18 行代码时,一定满足的条件不包括( )。
A. j≤ij \le ij≤i
B. a[i]−a[j]>ka[i]-a[j] \gt ka[i]−a[j]>k
C. j≤nj \le nj≤n
D. a[j]<a[i]a[j]\lt a[i]a[j]<a[i]
答案解析:B
对第一个数而言j肯定是0,因为自己减自己等于0
对第二个数字而言如果a[2]-a[1]>k,j走到1(也就是i-1),a[2]-a[2]=0,因为k>0则有j<i,因为i<=n,所以j小于n
对第一个数字而言,j=0,i=1,a[1]-a[0]=a[1]-0,a[1]-0(也就是a[i]-a[j])不一定大于k
因为排序去重了,所以 a[j]<a[i]
- 当输入的n=100、k=2、a={1,2,...,100}n=100 、k=2 、a=\{1,2,...,100\}n=100、k=2、a={1,2,...,100}时,输出为( )。
A. 34
B. 100
C. 50
D. 33
答案解析:A
每个区间内最大数-最小数最大可以为2,那么【1】,【2,3,4】,【5,6,7】,…,【98,99,100】,共34组
- 假设输入的 a 数组和 k 均为正整数,但 a 数组不一定有序,若误删去第13行的 std::sort(a+1,a+n+1);,程序有可能出现的问题有( )。
A. 输出的答案比原本答案更大
B. 输出的答案比原本答案更小
C. 出现死循环行为
D. 以上均可能发生
答案解析:B
对于纯逆序来说,比如3 2 1,除了第一个数字每个数字与之前的数字相减会变负数,所以组数会变小
(3)
#include <algorithm>
#include <cstdio>
#include <cstring>
#define ll long long
int f[5007][5007];
int a[5007], b[5007];
int n;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
}
for (int i = 1; i <= n; ++i) {
scanf("%d", &b[i]);
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
f[i][j] = std::max(f[i][j], std::max(f[i - 1][j], f[i][j - 1]));
if (a[i] == b[j]) {
f[i][j] = std::max(f[i][j], f[i - 1][j - 1] + 1);
}
}
}
printf("%d\n", f[n][n]);
return 0;
}
判断题
- 当输入“4 1 2 3 4 1 3 2 2”时,输出为2。( )
对
错
答案解析: ✓\checkmark✓
【1,2,3,4】【1,3,2,2】的最长公共子序列为【1,3】
- 当程序运行完毕后,对于所有的1≤i,j≤n1 \le i,j \le n1≤i,j≤n,都一定有f[i][j] <= f[n][n]。( )
对
错
答案解析: ✓\checkmark✓
整体最优 f[n][n] 一定大于等于任何前缀
- 将第18行的f[i][j] = std::max(f[i][j], std::max(f[i - 1][j], f[i][j - 1]));删去后,并不影响程序运行结果。( )
对
错
答案解析:X
//传递上侧与左侧答案
f[i][j] = std::max(f[i][j], std::max(f[i - 1][j], f[i][j - 1]));
//相同时传递左上角答案+1
if (a[i] == b[j])f[i][j] = std::max(f[i][j], f[i - 1][j - 1] + 1);
删去与上、左取最大值会使 DP 无法正确传递,答案改变
单选题
4. 输出的答案满足的性质有( )。
A. 小于等于 n
B. 大于等于 0
C. 不一定大于等于 1
D. 以上均是
答案解析:D
A肯定
B如果没有公共的部分则答案为0
C说的没错
- 如果在16行的循环前加上以下两行:std::sort(a + 1, a + n + 1);std::sort(b + 1, b + n + 1);,则答案会( )。
A. 变大或不变
B. 变小或不变
C. 一定变大
D. 不变
答案解析:A
不变是有可能的,【1,2】排序后【1,2】
变大是有可能的,【1,2】排序后【2,1】,变之前f[n][n]=1,变之后=2
不会变小
- 如果输入的a={1,2,...,n}\{1,2,...,n\}{1,2,...,n},而且b数组中数字均为1~n中的正整数,则上述代码等价于下面哪个问题:( )。
A. 求 b 数组去重后的长度
B. 求 b 数组的最长上升子序列
C. 求 b 数组的长度
D. 求 b 数组的最大值
答案解析:B
因为b可能无序,但是a有序,求最长公共子序列时b中被挑选的元素一定单调不降,所以求最长上升子序列
ACD无道理
三、完善程序(单选题,每小题3分,共计30分)
(1)字符串解码
“行程长度编码”(Run-Length Encoding)是一种无损压缩算法,常用于压缩重复字符较多的数据,以减少存储空间。假设原始字符串不包含数字字符,压缩规则如下:
● i) 如果原始字符串中一个字符连续出现N次(N≥2N \ge 2N≥2),在压缩字符串中它被表示为“字符+数字N”。例 如,编码“A12”代表12个连续的字符A。
● ii) 如果原始字符串中一个字符只出现1次,在压缩字符串中表示为该字符本身。例如,编码“B”代表1 个字符B。
以下程序实现读取压缩字符串并输出其原始的、解压后的形式,试补全程序。
#include <cctype>
#include <iostream>
#include <string>
using namespace std;
int main() {
string z;
cin >> z;
string s = "";
for (int i = 0; i < z.length(); ) {
char ch = z[i];
if (① && isdigit(z[i + 1])) {
i++;
int count = 0;
while (i < z.length() && isdigit(z[i])) {
count = ②;
i++;
}
for (int j = 0; j < ③; ++j) {
s += ch;
}
} else {
s += ④;
⑤;
}
}
cout << s << endl;
return 0;
}
- ①处应填( )
A. i < z.length()
B. i - 1 >= 0
C. i + 1 < z.length()
D. isdigit(z[i])
答案解析:C
如果【i+1】位不是数字的话,那么将当前字符拼到s里面去,如果当前位已经是最后一个字母的话,直接去拼字符串,保守做法C。
- ②处应填( )
A. count + (z[i]-‘0’)
B. count * 10 + (z[i]-‘0’)
C. z[i] - ‘0’
D. count + 1
答案解析:B
秦九韶算法,当前数字扩大进制倍加上下一个数字,一位z[i]是字符所以-‘0’。
- ③处应填( )
A. count - 1
B. count
C. 10
D. z[i] - ‘8’
答案解析:B
重复 count 次该字符。
- ④处应填( )
A. z[i + 1]
B. ch
C. z.back()
D. (char)z[i] + 1
答案解析:B
如果单次出现直接将字符加入当前字符串。
- ⑤处应填( )
A. i–
B. i = i + 2
C. i++
D. //不执行任何操作
答案解析:C
大循环没写i++,需要手动移动。
(2)精明与糊涂
有N个人,分为两类:
● i) 精明人:永远能正确判断其他人是精明还是糊涂;
● ii) 糊涂人:判断不可靠,会给出随机的判断。
已知精明人严格占据多数,即如果精明人有k个,则满足k>N/2k > N/2k>N/2 。
你只能通过函数query(i,j) 让第 i 个人判断第 j 个人:返回true表示判断结果为“精明人”;返回false表示判断结果为“糊涂人”。你的目标是通过互相判断,找出至少一个百分之百能确定的精明人。同时,你无需关心 query(i,j)的内部实现。
以下程序利用“精明人占多数”的优势,通过“消除”过程让人们互相判断并进行抵消,经过若干轮抵消后,最终留下的候选者必然属于多数派,即精明人。
例如,假设有三个人 0、1、2。如果0说1是糊涂人,而1也说0是糊涂人,则0和1至少有一个是糊涂人。程序将同时淘汰0和1。由于三人里至少有两个精明人,我们确定2是精明人。
试补全程序 。
#include <iostream>
#include <vector>
using namespace std;
int N;
bool query(int i, int j);
int main() {
cin >> N;
int candidate = 0;
int count = ①;
for (int i = 1; i < N; ++i) {
if (②) {
candidate = i;
count = 1;
} else {
if (③) {
④;
} else {
count++;
}
}
}
cout << ⑤<< endl;
return 0;
}
- ①处应填( )
A. 0
B. 1
C. N
D. -1
答案解析:B
可以想象用每一个精明人与糊涂人1v1消除的想法,因为精明人占多数,所以最后剩下来的一定是精明人,如果只有一个人,那么无法判断,直接保存第一个人为候选,总个数=1。
- ②处应填( )
A. count < 0
B. count == 1
C. count == 0
D. query(candidate, i) == false
答案解析:C
看到下面的程序是candidate = i;count = 1;重置了候选人与个数,说明已经没有可用候选人了,需要重置候选人与人数。
- ③处应填( )
A. query(candidate, i) == false
B. query(i, candidate) == true
C. query(candidate, i) == false && query(i, candidate) == false
D. query(candidate, i) == false || query(i, candidate) == false
答案解析:
else里面是++,说明if的情况是发现了某人说某人是糊涂人,这个时候我们的想法是成对抵消,用聪明人与糊涂人抵消或者糊涂人与糊涂人抵消。
- ④处应填( )
A. count–
B. break
C. count++
D. candidate = i
答案解析:
可用的候选个数减少一个。
- ⑤处应填( )
A. N - 1
B. count
C. candidate
D. 0
答案解析:C
输出最终的候选人。





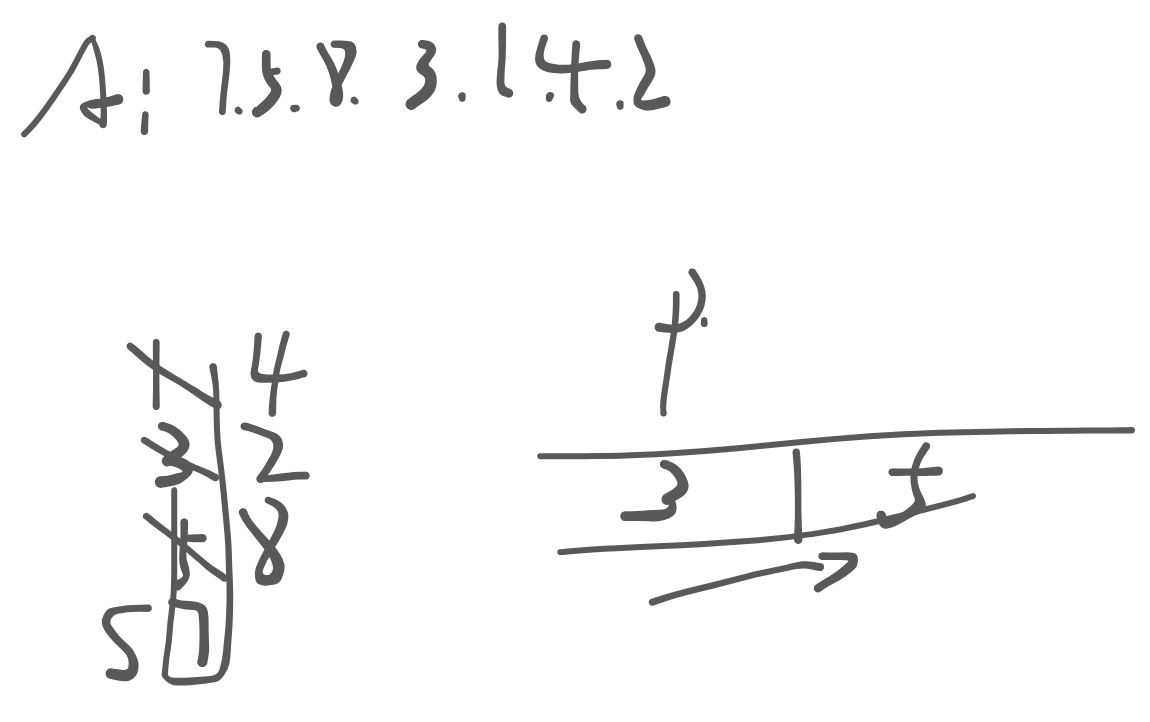
















 8975
8975

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








