IMU数据处理与位置计算实战

本文还有配套的精品资源，点击获取

简介：IMU（惯性测量单元）是能够测量三维空间中物体的线加速度和角速度的传感器，广泛用于多个领域。本文将详细解析如何利用IMU数据计算出经纬度坐标和高度信息，包括数据融合、姿态解算、位移积分和坐标转换等步骤。文章还将探讨如何通过优化算法提高定位精度和系统稳定性，以及在没有外部定位信号的情况下实现精确自主导航和运动跟踪的重要性。

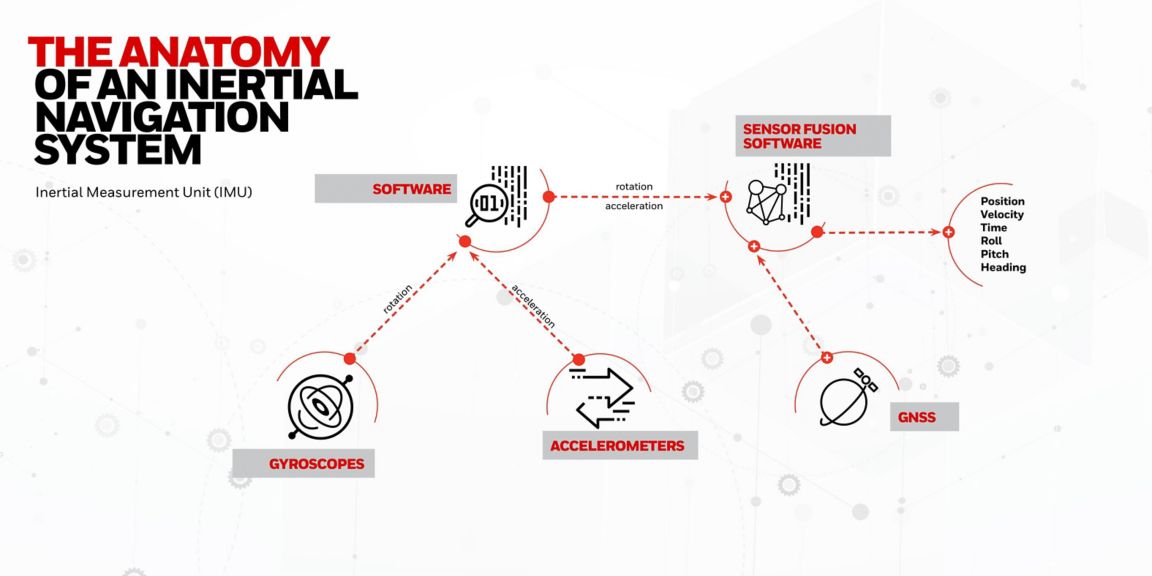
1. IMU传感器介绍

惯性测量单元（IMU）是用于测量和报告特定物体三维方向上加速度、角速度以及磁场的传感器系统。IMU广泛应用于航空、航天、机器人技术、虚拟现实、手机等移动设备，以实现定位、导航和稳定的控制。在深入了解IMU之前，我们需先认识其核心组成部分：加速度计和陀螺仪。

IMU的核心功能依赖于加速度计和陀螺仪的数据，它们分别负责检测线性加速度和角速度。加速度计能够测量传感器自身沿三维空间的加速度变化，而陀螺仪则负责测量围绕三个主轴的旋转速率。传感器的性能参数和误差特征，直接影响到数据的准确性与后续的数据融合算法效率。

IMU的标定对于提高系统整体性能至关重要。标定过程可确保传感器在实际应用中能提供准确的数据。标定技术包括静态和动态标定，它们能够修正传感器固有的偏差和校正环境因素带来的影响，从而提升整体系统的准确度和可靠性。

2. 加速度计和陀螺仪数据处理

2.1 基础数据获取

加速度计和陀螺仪是IMU（惯性测量单元）的核心传感器，负责提供设备运动状态的精确数据。理解这些数据的基础获取方式，对于后续的数据处理和应用至关重要。

2.1.1 加速度计的工作原理

加速度计能够测量物体的线性加速度，其工作原理基于牛顿第二运动定律（F=ma）。它通常由一组固定在某一轴上的质量块、弹簧以及位移测量装置组成。当物体加速时，质量块会由于惯性作用相对于周围结构产生位移，通过测量这个位移，加速度计可以计算出加速度值。

graph LR
A[加速度计感应组件] -->|物体加速度| B[质量块位移]
B -->|弹簧力与位移成正比| C[位移测量装置]
C -->|输出位移信号| D[加速度值计算]

2.1.2 陀螺仪的工作原理

陀螺仪则用于测量物体角速度，其核心是一个高速旋转的转子或光束，保持在特定的轴向。当外部环境使陀螺仪旋转时，根据角动量守恒原理，转子或光束会尝试维持其旋转轴方向不变，这个效应即为“陀螺效应”。通过检测转子或光束方向的微小变化，可以得到相应的角速度测量值。

graph LR
A[外部角速度] -->|作用于陀螺仪| B[转子/光束偏移]
B -->|陀螺效应| C[转子/光束保持方向]
C -->|偏移角度测量| D[角速度计算]

2.2 数据预处理

数据预处理是IMU数据处理的一个重要步骤，它通过滤波和去噪方法提高数据质量，为后续处理奠定基础。

2.2.1 去噪和滤波方法

传感器数据往往含有噪声，这些噪声可能来源于传感器内部的电子噪声，也可能来自于外部环境的干扰。去噪和滤波技术是减少噪声影响的有效手段。常用的滤波方法包括低通滤波器、高通滤波器和带通滤波器。它们根据特定的频率范围对信号进行过滤，以达到去噪的目的。

一个常见的低通滤波器实现示例如下：

# Python实现一个简单的一阶低通滤波器
alpha = 0.1  # 滤波系数
filtered_value = alpha * current_value + (1 - alpha) * prev_filtered_value

2.2.2 采样率的选择和影响

采样率，即单位时间内采集数据的频率，对数据质量和处理效率都有重要影响。一个较高的采样率可以捕获更多的动态变化细节，但同时也会增加数据量，对存储和处理能力提出更高要求。在实际应用中，需要根据具体场景的需求和设备的处理能力综合考虑采样率的选择。

2.3 数据标定技术

数据标定是确保数据准确性的关键步骤，它包括设备的校准和数据的校正，确保传感器输出与实际物理量之间的一致性。

2.3.1 静态标定过程

静态标定是指在没有外部运动和干扰的条件下对传感器进行标定的过程。它通常涉及到一系列已知的参考点，传感器在此环境下获取数据，通过计算可以得到传感器的偏移量和比例因子，从而校准传感器输出。

2.3.2 动态标定的影响因素

动态标定则是在有运动变化的条件下进行的标定，这比静态标定复杂，因为它涉及到运动状态的改变。在动态标定过程中，需要考虑加速度、振动、温度变化等因素的影响，这些因素可能会引起传感器输出的偏差，因此动态标定比静态标定需要更多的技术和设备支持。

通过以上的介绍，我们可以看到，从基础数据获取到数据预处理，再到数据标定技术，每一步都是IMU数据处理不可或缺的环节。它们共同构成了IMU数据处理的基础框架，为后续的复杂应用和深入分析提供了坚实的基础。

[注：此为示例内容，实际撰写时需根据章节顺序、结构深度以及内容丰富度进行详细扩展。]

3. 数据融合技术

3.1 卡尔曼滤波器基础

3.1.1 卡尔曼滤波器原理

卡尔曼滤波器是一种高效的递归滤波器，它能够从一系列的含有噪声的测量中估计动态系统的状态。卡尔曼滤波器的核心思想是利用系统的动态模型和测量模型，通过预测和更新两个过程来实现对系统的估计。

在数学上，卡尔曼滤波器通过以下步骤来更新状态估计：

1. 预测（Predict）：根据系统的动态模型对当前状态进行预测。
2. 更新（Update）：当新的测量数据到来时，根据测量数据对预测结果进行修正。

这个过程可以用以下公式来表达：

• 预测阶段：
  ( \hat{x} {k|k-1} = F_k \hat{x} {k-1|k-1} + B_k u_k )（预测状态）
  ( P_{k|k-1} = F_k P_{k-1|k-1} F_k^T + Q_k )（预测误差协方差）

• 更新阶段：
  ( K_k = P_{k|k-1} H_k^T (H_k P_{k|k-1} H_k^T + R_k)^{-1} )（卡尔曼增益）
  ( \hat{x} {k|k} = \hat{x} {k|k-1} + K_k (z_k - H_k \hat{x} {k|k-1}) )（更新状态）
  ( P {k|k} = (I - K_k H_k) P_{k|k-1} )（更新误差协方差）

在这些公式中：

• ( \hat{x}_{k|k-1} ) 是在时间 k 基于时间 k-1 的信息所做的状态预测。
• ( P_{k|k-1} ) 是预测状态的误差协方差。
• ( K_k ) 是卡尔曼增益，它体现了测量数据相对于预测数据的重要性。
• ( \hat{x}_{k|k} ) 是在时间 k 基于所有可用信息（包括新的测量 z_k）的状态更新。
• ( P_{k|k} ) 是更新后状态的误差协方差。

3.1.2 状态估计与误差协方差更新

在卡尔曼滤波器中，状态估计的准确性是通过误差协方差来度量的。误差协方差 ( P ) 是一个矩阵，它反映了状态估计的不确定性和误差。

更新过程包括两个主要步骤：

1. 预测误差协方差 ( P_{k|k-1} )：在没有新的测量数据的情况下，预测下一时刻的误差协方差。

2. 更新误差协方差 ( P_{k|k} )：在获得新的测量数据后，根据卡尔曼增益和测量残差来更新误差协方差。

误差协方差的更新反映了滤波器如何在预测和更新步骤之间平衡对系统状态的估计。卡尔曼滤波器的优势在于，它不仅提供了一个估计值，而且还提供了一个误差协方差，这个协方差可以帮助我们了解估计值的可信程度。

为了更好地理解卡尔曼滤波器的工作原理，我们可以考虑一个简单的一维动态系统例子。在这个例子中，状态更新和测量可以表示为以下形式：

状态方程：( x_k = x_{k-1} + w_{k-1} )
测量方程：( z_k = x_k + v_k )

其中，( x_k ) 是当前时刻的状态，( x_{k-1} ) 是前一时刻的状态，( w_{k-1} ) 是过程噪声，( z_k ) 是测量值，( v_k ) 是测量噪声。

在实际应用中，为了实现卡尔曼滤波器，需要对动态系统进行建模，确定系统矩阵 ( F_k )，控制输入矩阵 ( B_k )，测量矩阵 ( H_k )，过程噪声协方差 ( Q_k )，以及测量噪声协方差 ( R_k )。这些参数的设置对于滤波器的性能至关重要。

3.2 互补滤波器应用

3.2.1 互补滤波器原理

互补滤波器是一种简单有效的数据融合技术，特别适用于频率不匹配的传感器数据融合，如将陀螺仪与加速度计的数据结合起来估计角度或角速度。

互补滤波器的基本思想是利用低频信号的稳定性与高频信号的快速响应性来互补各自的优点。具体来说，互补滤波器使用一个低通滤波器对加速度计数据进行滤波，获取静态倾角信息；同时使用一个高通滤波器对陀螺仪数据进行滤波，获取动态旋转信息。然后，根据设定的权重参数，将这两种滤波后的信号进行加权求和，得到最终的角度估计。

数学表达如下：

• 高频滤波器（陀螺仪）：( \theta_{gyro} = \theta_{gyro} + \omega \Delta t )
• 低频滤波器（加速度计）：( \theta_{acc} = LPF(\theta_{acc}) )
• 互补滤波器输出：( \theta = \alpha \theta_{gyro} + (1 - \alpha) \theta_{acc} )

其中，( \theta_{gyro} ) 和 ( \theta_{acc} ) 分别是陀螺仪和加速度计输出的角度值，( \omega ) 是陀螺仪的角速度测量值，( \Delta t ) 是采样周期，( \alpha ) 是一个介于 0 和 1 之间的权重参数，( LPF ) 是低通滤波器函数。

3.2.2 应用场景与优势分析

互补滤波器广泛应用于飞行器、机器人和增强现实（AR）等领域的姿态估计。它之所以受到青睐，主要是因为其算法简单、计算效率高，并且易于实现。

应用场景：

1. 无人机控制 ：通过互补滤波器融合陀螺仪和加速度计数据，能够实时准确地估计飞行器的姿态，帮助实现稳定飞行。

2. 穿戴设备 ：在智能手表、健身追踪器等穿戴设备中，互补滤波器可以用来跟踪用户的运动，并提供姿态信息。

3. 移动机器人 ：机器人使用互补滤波器可以在复杂多变的环境中进行平衡和导航。

优势分析：

1. 低计算复杂度 ：相比于卡尔曼滤波器，互补滤波器对计算资源的要求更低，这在资源受限的嵌入式设备中尤为重要。

2. 抗噪声能力 ：通过调整低通和高通滤波器的截止频率和权重参数，互补滤波器可以很好地抑制噪声。

3. 快速响应性 ：在高权重参数时，互补滤波器能够快速响应加速度计的变化，从而获得较好的动态性能。

4. 易用性 ：互补滤波器的参数调整相对简单，便于开发人员根据具体应用进行优化。

需要注意的是，互补滤波器也有其局限性。它通常假设加速度计数据中没有由于动态运动引起的高频成分，这在某些应用场景中可能不成立。因此，选择使用互补滤波器还是其他更复杂的滤波技术，需要根据应用的特定需求和环境条件来决定。

3.3 多传感器融合策略

3.3.1 系统模型的建立

在进行多传感器数据融合时，第一步是建立一个准确的系统模型。系统模型是描述传感器如何与被观测环境相互作用的数学表示。一个基本的系统模型包括系统的动态模型和观测模型。

• 动态模型 ：描述了系统随时间的变化规律，通常用状态空间模型表示，包括状态转移方程和控制输入方程。状态转移方程描述了在没有外部输入的情况下，系统状态如何随时间变化；控制输入方程则描述了如何将外部控制输入转化为系统状态的变化。

• 观测模型 ：定义了系统状态与传感器测量值之间的关系。测量模型通常依赖于传感器的特性，包括其测量范围、精确度、噪声特性等。

在多传感器融合中，最常用的系统模型是扩展卡尔曼滤波器（EKF）和无迹卡尔曼滤波器（UKF）。扩展卡尔曼滤波器是对标准卡尔曼滤波器的扩展，它通过线性化非线性系统方程来近似处理非线性问题。无迹卡尔曼滤波器则是通过一组确定性采样点来捕捉非线性函数的统计特性，从而进行非线性估计。

3.3.2 数据融合算法的选择与优化

选择合适的数据融合算法对于最终的融合效果至关重要。算法的选择依赖于多个因素，包括但不限于传感器的类型、精度、噪声特性，以及系统的动态特性。

算法选择

• 卡尔曼滤波器 ：适用于线性系统或者可以通过线性化近似处理的非线性系统。由于其递归性，卡尔曼滤波器在处理时序数据上具有优势。

• 粒子滤波器 ：适用于非线性或非高斯噪声系统。粒子滤波器通过一组随机样本（粒子）来表示概率分布，可以处理更复杂的系统模型。

• 信息融合方法 ：例如分布式卡尔曼滤波器、联邦卡尔曼滤波器等，适用于多个传感器分布在不同地理位置的情况。

算法优化

• 噪声模型的校准 ：确保传感器噪声和过程噪声模型的准确性对于提高融合算法的性能至关重要。

• 初始化与参数调整 ：合理地初始化状态估计和协方差，以及调整滤波器的参数（如卡尔曼增益、粒子权重等），可以优化融合结果。

• 融合策略 ：选择合适的融合策略，如集中式融合、分布式融合或分层融合，以适应特定的应用需求。

• 硬件优化 ：使用更适合的硬件平台，如多核处理器或专用硬件加速器，可以提高数据处理速度，降低算法的延迟。

代码实例

import numpy as np
from scipy.linalg import expm, block_diag

# 假设F为状态转移矩阵，H为观测矩阵，Q为过程噪声协方差，R为测量噪声协方差
F = np.array([[1, 1], [0, 1]])  # 示例状态转移矩阵
H = np.array([[1, 0]])  # 示例观测矩阵
Q = np.eye(2) * 0.01  # 示例过程噪声协方差
R = np.eye(1) * 0.1  # 示例测量噪声协方差

# 构造初始状态和初始协方差矩阵
x = np.array([[0], [0]])  # 初始状态
P = block_diag(np.eye(2), np.eye(2))  # 初始协方差矩阵

# 预测和更新函数（简化的EKF过程）
def predict(x, P, F, Q):
    """预测步骤"""
    x = F @ x
    P = F @ P @ F.T + Q
    return x, P

def update(x, P, z, H, R):
    """更新步骤"""
    y = z - H @ x  # 计算测量残差
    S = H @ P @ H.T + R  # 计算残差协方差
    K = P @ H.T @ np.linalg.inv(S)  # 计算卡尔曼增益
    x = x + K @ y  # 更新状态估计
    P = (np.eye(2*2) - K @ H) @ P  # 更新误差协方差
    return x, P

# 运行一次预测和更新过程的示例
x, P = predict(x, P, F, Q)
x, P = update(x, P, np.array([[1]]), H, R)

在这个代码示例中，我们简要地实现了一个扩展卡尔曼滤波器的预测和更新步骤。需要注意的是，实际应用中的状态转移矩阵F和观测矩阵H可能要复杂得多，并且需要根据实际问题进行调整。

为了处理复杂的非线性问题，我们可能需要使用更高级的技术，比如无迹卡尔曼滤波器（UKF），该技术通过使用Sigma点来避免线性化带来的误差。

4. 姿态解算方法

姿态解算是IMU传感器应用中的核心技术之一，广泛应用于机器人、航空航天、无人机和虚拟现实等领域。姿态信息能够帮助我们了解设备的朝向和旋转状态，这对于维持平衡、导航定位以及用户交互体验至关重要。解算出准确的姿态信息，需要理解不同的表示方法，掌握高效的解算算法，并且进行细致的误差分析与补偿。

4.1 姿态表示方法

4.1.1 欧拉角与四元数的对比

在讨论姿态表示方法时，欧拉角和四元数是两种最常见的方法。欧拉角是一种简单的表示方法，通过三个角度来描述三维空间中的旋转，易于理解和计算。然而，欧拉角存在万向节锁（Gimbal Lock）的问题，当两个旋转轴对齐时，会丢失一个自由度，导致无法通过增加旋转角度来描述所有的旋转状态。

相比之下，四元数是一种四维复数，可以避免万向节锁，并且能够更高效地进行旋转计算。四元数由一个实数部分和三个虚数部分组成，表示为 (q = w + xi + yj + zk)。四元数的这种表示方法可以保证在连续旋转时，始终保持一个单一且连续的旋转路径。

4.1.2 姿态更新与插值技术

在实际应用中，姿态需要频繁更新以反映设备的实时状态。四元数插值技术（如球面线性插值SLERP）能够平滑地在两个四元数之间插值，非常适合在动态场景下维持连续的旋转路径。通过四元数插值，可以在保持旋转轴不变的前提下，平滑地改变旋转速度。

4.2 姿态解算算法

4.2.1 静态姿态解算

静态姿态解算是指在没有加速度影响的情况下，仅使用陀螺仪进行的姿态估计。在这种情况下，陀螺仪的数据可以被直接积分以获得旋转角度。由于陀螺仪输出的是角速度，因此将角速度积分得到的姿态角需要通过某种形式的反馈校准来消除累积误差。

import numpy as np

# 假设gyro_data为陀螺仪输出的角速度数组
# dt为积分的时间间隔，单位为秒

def integrate_gyro(gyro_data, dt):
    angles = []
    theta = np.zeros(3)  # 初始化角度为零
    for rate in gyro_data:
        theta += rate * dt  # 角速度积分得到角度变化
        angles.append(theta)
    return angles

# 以下为示例数据和函数调用
# gyro_data = [0.1, -0.2, 0.1]  # 三个轴的角速度示例
# angles = integrate_gyro(gyro_data, 0.01)  # 假设积分时间为0.01秒

4.2.2 动态姿态解算技术

动态姿态解算通常会结合加速度计和陀螺仪的数据，利用卡尔曼滤波器或互补滤波器等方法，来提高姿态估计的准确性和稳定性。与静态解算相比，动态解算在处理过程中需要考虑外部加速度对姿态的影响，因此需要对数据进行更复杂的处理。

4.3 姿态解算中的误差分析

4.3.1 误差来源与分类

在姿态解算过程中，误差来源可分为两类：静态误差和动态误差。静态误差主要来源于传感器本身，如传感器的零偏、噪声、非线性误差等；动态误差则是由设备的运动引起，例如由于加速度引起的姿态误差。

4.3.2 误差补偿策略

误差补偿是提高姿态解算精度的关键步骤。常见的补偿策略包括标定传感器，以获取和校正零偏和噪声；使用先进的滤波算法来平滑数据并减少噪声影响；以及设计更复杂的动态误差模型来预测和补偿动态误差。

为了有效实施误差补偿策略，可以采取以下步骤：
1. 通过静态和动态测试收集传感器数据。
2. 利用数学模型分析误差的特性。
3. 应用补偿算法，比如在线性模型中应用偏置校正，在动态模型中应用卡尔曼滤波器。
4. 通过实验验证补偿效果。

graph TD;
    A[开始] --> B[数据收集]
    B --> C[误差分析]
    C --> D[误差模型建立]
    D --> E[补偿算法设计]
    E --> F[补偿效果验证]
    F --> G[结束]

上述流程图展现了从开始到结束的误差补偿过程，每一步都是为了得到更准确的姿态解算结果。通过这个流程，我们可以系统地对误差进行分析和补偿，最终达到提高整个系统的稳定性和精确度的目的。

5. 位移积分与定位误差校正

5.1 位移积分原理

5.1.1 位移积分的方法

在应用IMU传感器进行运动跟踪时，位移积分是一种根据速度和时间计算位移的方法。位移积分的关键在于准确获得速度信息。通常情况下，速度信息可以通过对加速度计数据进行积分得到。

为确保位移积分的准确性，需要采用正确的积分方法，常见的方法包括：

• 离散积分：对于离散的加速度数据，可以通过数值积分方法（如梯形法则、辛普森法则）来计算位移。
• 连续积分：理论上，如果加速度数据是连续且平滑的，可以通过解析方式直接积分得到速度和位移。
• 过滤后的积分：在实际应用中，通常使用低通滤波器处理后的加速度数据进行积分，以降低噪声影响。

下面的代码示例演示了如何通过离散梯形法则积分加速度数据得到速度和位移：

import numpy as np

def trapezoidal_integration(acc, dt):
    """
    使用梯形法则对加速度进行位移积分

    :param acc: 加速度数据数组，单位 m/s^2
    :param dt: 时间间隔，单位 s
    :return: 速度和位移数据数组
    """
    vel = np.cumsum(acc * dt)
    disp = np.cumsum(vel * dt)
    return vel, disp

# 示例数据
acc = np.array([0, 1, 2, 3, 4, 5])  # 加速度数据示例
dt = 0.1  # 时间间隔示例

# 进行位移积分
velocity, displacement = trapezoidal_integration(acc, dt)

print("速度: ", velocity)
print("位移: ", displacement)

在上述代码中，我们首先定义了一个 trapezoidal_integration 函数，它接受加速度数据数组和时间间隔，然后通过 np.cumsum 函数实现了梯形积分，得到速度和位移数据。

5.1.2 积分误差的来源

位移积分过程中可能会产生多种误差，主要包括：

• 初始条件误差：如果初始速度或位置不确定，将导致整体位移积分产生偏差。
• 加速度测量误差：传感器本身的噪声和非线性特性会造成加速度测量误差。
• 离散化误差：离散积分是近似连续积分，当采样率不足时，会导致较大误差。
• 数值积分方法误差：不同的数值积分方法会产生不同大小的误差。

5.2 定位误差校正技术

5.2.1 系统偏差校正

系统偏差校正是确保传感器数据准确性的关键步骤。偏差校正通常包括以下几个方面：

• 硬件校正：调整传感器的物理位置或角度以消除硬件安装偏差。
• 软件校正：通过算法对数据进行校正，这包括对传感器数据进行标定，消除系统误差。
• 环境补偿：针对特定环境因素（如温度、气压）进行补偿，修正测量数据。

在软件校正方法中，常见的做法是建立一个校正模型，将传感器的原始数据映射到校正后的数据。例如，通过建立加速度计和陀螺仪的零偏校正模型，来补偿其静止状态下的输出误差。

5.2.2 实时误差补偿方法

对于实时系统，采用实时误差补偿技术可以显著提高定位精度。实时误差补偿通常包括：

• 在线校准：通过不断采样和分析数据，实时调整校正模型的参数。
• 状态反馈控制：采用控制理论中的反馈机制，将误差信息反馈到传感器系统，动态调节输出。

下面的代码示例演示了在线校准过程中调整传感器零偏的方法：

# 假设acc_raw是原始加速度数据，陀螺仪数据gyro_raw类似
# acc_calib是校正后的加速度数据，acc_offset是零偏校正参数

acc_offset = np.array([0.01, -0.02, 0.01])  # 初始零偏校正参数

for i in range(len(acc_raw)):
    acc_calib[i] = acc_raw[i] - acc_offset  # 校正零偏

    # 实时更新零偏校正参数
    # 假设我们有一个函数可以实时估计零偏
    acc_offset = estimate_zero_offset(acc_calib[i], dt)

在上述代码中，我们使用一个零偏校正参数 acc_offset 对原始加速度数据进行校正。同时，假设有一个 estimate_zero_offset 函数能够实时估计并更新零偏校正参数，从而实现在线校准。

5.3 精度评估与提升

5.3.1 精度评估方法

精度评估是任何测量系统不可或缺的一部分。通常采用以下方法评估IMU的定位精度：

• 基准比较：将IMU系统与其他已知精度更高的系统（例如GPS）进行比较，通过统计分析来评估误差。
• 多次重复测量：对同一路径进行多次测量，然后计算平均值和标准偏差来评估系统的稳定性。
• 统计测试：使用各种统计分析方法（如误差分布、置信区间）来分析定位误差。

5.3.2 精度提升策略与案例分析

为了提升IMU定位精度，可以采取以下策略：

• 硬件升级：改进传感器硬件设计，比如采用更高精度的陀螺仪和加速度计。
• 数据融合：使用多传感器数据融合技术（如卡尔曼滤波器）来综合不同传感器的优势，减少单一传感器的误差。
• 算法优化：改进滤波算法和校准算法，通过深度学习等先进技术进行误差预测和校正。

下面的表格展示了不同策略对IMU定位精度的影响：

策略类别	描述	预期效果	优势	劣势
硬件升级	更换为高精度传感器	提高静态和动态精度	长期稳定性好	成本增加
数据融合	使用多传感器融合技术	减少环境干扰	抗干扰性强	实时性降低
算法优化	改进滤波和校准算法	提升系统响应速度	实时性强	需要专业人员设计

通过分析这些策略，结合实际应用场景，可以有效提升IMU的定位精度。例如，在一个移动机器人导航系统中，通过引入高精度的陀螺仪和使用先进的卡尔曼滤波算法，实现了对机器人位置和姿态的准确估计，显著提升了导航精度。

6. 地理坐标系转换

6.1 坐标系基础知识

6.1.1 地理坐标系与地心坐标系

在空间定位和导航领域，不同的地理坐标系被用来描述地球表面上的点。地理坐标系通常指的是基于地球表面特征的坐标系统，最常见的包括经纬度坐标系。在这一坐标系中，点的位置由其经度、纬度以及高度来定义。经度和纬度分别对应于东西和南北方向的角度测量，从赤道和本初子午线开始计算。

地心坐标系是以地球的质心作为坐标原点的坐标系统，常用的是地心地固坐标系（Earth-Centered, Earth-Fixed, ECEF）。在这种坐标系中，所有的坐标点都相对于地球中心来定义，因此这种坐标系不受地球自转的影响，非常适合用于全球定位系统（GPS）等应用，因为它可以提供全球统一的参考框架。

6.1.2 坐标系转换的基本原理

坐标转换通常是为了将一个坐标系下的点的位置表示转换到另一个坐标系中。这种转换通常依赖于一系列数学操作，如旋转、平移等。在地理坐标系转换中，我们经常需要进行旋转和平移操作，以将地理坐标（经度、纬度、高度）转换为地心坐标系下的X、Y、Z坐标。

例如，从地理坐标转换到地心地固坐标系可以通过以下步骤实现：

1. 将地理坐标（经度、纬度）转换为弧度。
2. 计算位置相对于地球质心的角度。
3. 应用旋转矩阵以考虑地球自转。
4. 考虑地球椭球模型进行平移。

代码示例：

import numpy as np

# 经纬度转弧度
def deg_to_rad(degrees):
    return degrees * np.pi / 180

# 经纬度和高度转ECEF坐标
def llh_to_ecef(lat, lon, h):
    R = 6378137  # WGS84椭球体的长半轴
    flattening = 1 / 298.257223563  # WGS84椭球体扁率
    N = R / np.sqrt(1 - flattening * (2 - flattening) * np.sin(lat)**2)
    x = (N + h) * np.cos(lat) * np.cos(lon)
    y = (N + h) * np.cos(lat) * np.sin(lon)
    z = ((1 - flattening)**2 * N + h) * np.sin(lat)
    return x, y, z

# 示例转换
lat = 40.7128 # 纬度
lon = -74.0060 # 经度
h = 10         # 高度（米）

x, y, z = llh_to_ecef(deg_to_rad(lat), deg_to_rad(lon), h)

在上述代码中，我们定义了将经纬度和高度转换为ECEF坐标点的函数 llh_to_ecef 。注意，这个例子使用的是WGS84椭球模型参数，实际应用中可根据具体情况进行调整。

6.2 坐标转换算法

6.2.1 欧拉角转换方法

欧拉角是描述刚体在三维空间中的方向的一种方法，其本质是通过三次旋转将一个坐标系下的点转换到另一个坐标系。对于地理坐标转换来说，常常使用三个欧拉角：偏航角（Yaw）、俯仰角（Pitch）、翻滚角（Roll）。这在航空和船舶的导航中特别常见。

代码示例：

def euler_to_rotation_matrix(yaw, pitch, roll):
    """
    生成基于欧拉角的旋转矩阵
    """
    cy, sy = np.cos(yaw), np.sin(yaw)
    cp, sp = np.cos(pitch), np.sin(pitch)
    cr, sr = np.cos(roll), np.sin(roll)

    R_x = np.array([[1, 0, 0],
                    [0, cp, -sp],
                    [0, sp, cp]])

    R_y = np.array([[cy, 0, sy],
                    [0, 1, 0],
                    [-sy, 0, cy]])

    R_z = np.array([[cp, -sp, 0],
                    [sp, cp, 0],
                    [0, 0, 1]])

    R = np.dot(R_z, np.dot(R_y, R_x))

    return R

6.2.2 四元数与旋转矩阵的应用

四元数是一种扩展了复数的数学工具，它包括一个实部和三个虚部，能够避免万向节锁问题，并能够以更加高效和准确的方式描述三维空间中的旋转。四元数特别适用于实时应用，如机器人、游戏和虚拟现实等。

代码示例：

import quaternion

def rotation_matrix_to_quaternion(rot_matrix):
    """
    将旋转矩阵转换为四元数
    """
    q = quaternion.from_rotation_matrix(rot_matrix)
    return q

# 示例：将上面欧拉角生成的旋转矩阵转换为四元数
R = euler_to_rotation_matrix(deg_to_rad(lat), deg_to_rad(lon), deg_to_rad(alt))
q = rotation_matrix_to_quaternion(R)

在上面的代码中，我们利用 quaternion 库中的 from_rotation_matrix 函数，将旋转矩阵转换为四元数。这样，在需要进行旋转操作时，使用四元数可以简化计算，并能确保更高的精度。

6.3 实际应用中的坐标转换

6.3.1 地图匹配与路径规划

在地图匹配和路径规划中，坐标系转换是关键步骤之一。地图通常基于地图制作者定义的特定坐标系，而用户设备或车辆可能使用GPS坐标（地心地固坐标系）。在进行路径规划或地图匹配时，需要将GPS坐标转换为地图坐标系，或者反之。

6.3.2 多传感器数据融合中的坐标转换实例

在使用多个传感器进行定位和导航时，不同传感器可能使用不同的坐标系统。例如，IMU传感器可能提供基于设备的局部坐标系下的加速度和角速度数据，而GPS提供地心地固坐标系下的位置数据。为了整合这些数据，需要通过坐标转换将它们转换到统一的坐标系中，通常为地心地固坐标系。

代码示例：

# 假设我们有来自GPS和IMU传感器的数据
gps_data = (lat, lon, h) # GPS提供的经纬度和高度
imu_data = (acc_x, acc_y, acc_z, gyro_x, gyro_y, gyro_z) # IMU数据

# 将GPS数据转换为ECEF坐标
x, y, z = llh_to_ecef(*gps_data)

# 将IMU数据转换到同一ECEF坐标系下（需要进行相应的传感器校准和对齐）
# 此步骤通常涉及到复杂的信号处理和校准算法，这里不展开

# 在统一的ECEF坐标系下进行数据融合和处理
# ...

在这个例子中，我们用GPS和IMU两个传感器的数据说明了坐标转换在多传感器数据融合中的应用。在实际操作中，需要进行一系列复杂的校准和处理步骤，才能将不同传感器的数据融合到一个统一的坐标系中，例如使用卡尔曼滤波器进行状态估计。

通过上述方法的应用和操作步骤的介绍，我们可以看出地理坐标系转换在多个领域的实用性和重要性。无论是地图匹配、路径规划还是多传感器数据融合，准确的坐标转换都是确保导航和定位精度的关键。

7. 高度信息的获取与计算

高度是导航、测绘及运动分析中不可或缺的数据之一。不论是航空飞行、登山探险，还是移动设备中的地图应用，高度信息都是重要的参考指标。获取准确的高度信息对很多应用场景至关重要，而高度误差的分析与校正则是保障高度数据质量的关键环节。接下来将围绕高度信息的测量原理、处理与应用，以及误差分析与校正进行深入探讨。

7.1 高度测量原理

7.1.1 海拔高度与相对高度的区别

在地理信息系统（GIS）中，高度分为两类：海拔高度和相对高度。海拔高度是相对于海平面的垂直距离，用来表示某个点的绝对高度。相对高度则指两点间的垂直高差，常用于描绘地形起伏和建筑物高度。IMU传感器主要测量的是相对高度，而在GPS定位中则可以获得海拔高度。

7.1.2 测量高度的方法与技术

测量高度的方法很多，使用IMU传感器时，常用的技术包括压力传感器（气压计）和雷达/激光测高。气压计根据大气压强与高度的关系来计算高度变化，而雷达或激光测高则是通过发射信号并接收反射信号的时间差来计算目标高度。

flowchart LR
A[开始高度测量] --> B[确定高度类型]
B --> C{是否使用IMU}
C -->|是| D[使用IMU传感器]
C -->|否| E[使用GPS]
D --> F[气压计法]
D --> G[雷达/激光测高]
E --> H[GPS定位法]
F --> I[计算气压差]
G --> J[时间差测高]
H --> K[解析GPS数据]
I --> L[海拔高度]
J --> M[相对高度]
K --> N[海拔高度]

7.2 高度信息的处理与应用

7.2.1 高度数据的滤波与平滑

在获取高度数据时，受到多种因素如风力、振动等影响，会出现数据噪声。应用滤波和平滑技术能有效减少噪声，提高数据的准确性。常用的滤波算法包括低通滤波器、卡尔曼滤波器和中值滤波器。

7.2.2 高度信息在导航中的应用

高度信息对于飞行器的三维导航尤为重要。在飞行器的航迹规划和姿态控制中，高度信息能帮助避免碰撞并确保安全飞行高度。在移动设备中，地图应用使用高度信息来提供地形视图和等高线信息，增强用户体验。

7.3 高度误差分析与校正

7.3.1 高度误差的来源分析

高度误差可能来源于多个方面，包括传感器的硬件限制、算法误差、环境因素（如气压变化）及GPS信号的多路径效应。要准确分析误差，需要对测量系统的整体性能有深入理解。

7.3.2 高度误差的校正方法与实践

校正高度误差通常需要结合多种数据源和校正技术。例如，可以使用GPS辅助气压计数据，结合地形数据库校正海拔误差；在室内外导航中，可以使用Wi-Fi或蓝牙信标辅助定位，减少GPS多路径效应带来的误差。

通过上述内容的阐述，可以看出高度信息在多领域应用中的重要性以及测量准确性的必要性。高度的测量、处理和校正不仅对技术实现有要求，更是提高服务质量和用户体验的关键环节。在后续章节中，我们将继续探讨如何通过系统集成和创新技术进一步提高高度数据的精确度和可靠性。

本文还有配套的精品资源，点击获取

简介：IMU（惯性测量单元）是能够测量三维空间中物体的线加速度和角速度的传感器，广泛用于多个领域。本文将详细解析如何利用IMU数据计算出经纬度坐标和高度信息，包括数据融合、姿态解算、位移积分和坐标转换等步骤。文章还将探讨如何通过优化算法提高定位精度和系统稳定性，以及在没有外部定位信号的情况下实现精确自主导航和运动跟踪的重要性。

本文还有配套的精品资源，点击获取