第五章 二叉树和基于树的DFS
在这一章节的学习中,我们将要学习一个数据结构——二叉树(Binary Tree),和基于二叉树上的搜索算法。
在二叉树的搜索中,我们主要使用了分治法(Divide Conquer)来解决大部分的问题。之所以大部分二叉树的问题可以使用分治法,是因为二叉树这种数据结构,是一个天然就帮你做好了分治法中“分”这个步骤的结构。
二叉树上的遍历法
定义
遍历(Traversal),顾名思义,就是通过某种顺序,一个一个访问一个数据结构中的元素。比如我们如果需要遍历一个数组,无非就是要么从前往后,要么从后往前遍历。但是对于一棵二叉树来说,他就有很多种方式进行遍历:
- 层序遍历(Level order)
- 先序遍历(Pre order)
- 中序遍历(In order)
- 后序遍历(Post order)
我们在之前的课程中,已经学习过了二叉树的层序遍历,也就是使用 BFS 算法来获得二叉树的分层信息。通过 BFS 获得的顺序我们也可以称之为 BFS Order。而剩下的三种遍历,都需要通过深度优先搜索的方式来获得。而这一小节中,我们将讲一下通过深度优先搜索(DFS)来获得的节点顺序,
二叉树上的分治法
分治法(Divide & Conquer Algorithm)是说将一个大问题,拆分为2个或者多个小问题,当小问题得到结果之后,合并他们的结果来得到大问题的结果。
在一棵二叉树(Binary Tree)中,如果将整棵二叉树看做一个大问题的话,那么根节点(Root)的左子树(Left subtree)就是一个小问题,右子树(Right subtree)是另外一个小问题。这是一个天然就帮你完成了“分”这个步骤的数据结构。
遍历法和分治法实战
二叉树的最大深度
既可遍历又可分治
判断平衡二叉树
分治法,多个return value时可以用resultType
判断二叉搜索树
中序遍历从小到大,或者分治法
递归,分治法,遍历法的联系与区别
联系
分治法(Divide & Conquer)与遍历法(Traverse)是两种常见的递归(Recursion)方法。
分治法解决问题的思路
先让左右子树去解决同样的问题,然后得到结果之后,再整合为整棵树的结果。
遍历法解决问题的思路
通过前序/中序/后序的某种遍历,游走整棵树,通过一个全局变量或者传递的参数来记录这个过程中所遇到的点和需要计算的结果。
两种方法的区别
从程序实现角度分治法的递归函数,通常有一个返回值,遍历法通常没有。
递归、回溯和搜索
什么是递归 (Recursion) ?
很多书上会把递归(Recursion)当作一种算法。事实上,递归是包含两个层面的意思的:
- 一种由大化小,由小化无的解决问题的算法。类似的算法还有动态规划(Dynamic Programming)。
- 一种程序的实现方式。这种方式就是一个函数(Function / Method / Procedure)自己调用自己。
与之对应的,有非递归(Non-Recursion)和迭代法(Iteration),你可以认为这两个概念是一样的概念(番茄和西红柿的区别)。不需要做区分。
什么是搜索 (Search)?
搜索分为深度优先搜索(Depth First Search)和宽度优先搜索(Breadth First Search),通常分别简写为 DFS 和 BFS。搜索是一种类似于枚举(Enumerate)的算法。比如我们需要找到一个数组里的最大值,我们可以采用枚举法,因为我们知道数组的范围和大小,比如经典的打擂台算法:
int max = nums[0];
for (int i = 1; i < nums.length; i++) {
max = Math.max(max, nums[i]);
}
枚举法通常是你知道循环的范围,然后可以用几重循环就搞定的算法。比如我需要找到 所有 x^2 + y^2 = K 的整数组合,可以用两重循环的枚举法:
// 不要在意这个算法的时间复杂度
for (int x = 1; x <= k; x++) {
for (int y = 1; y <= k; y++) {
if (x * x + y * y == k) {
// print x and y
}
}
}
而有的问题,比如求 N 个数的全排列,你可能需要用 N 重循环才能解决。这个时候,我们就倾向于采用递归的方式去实现这个变化的 N 重循环。这个时候,我们就把算法称之为搜索。因为你已经不能明确的写出一个不依赖于输入数据的多重循环了。
通常来说 DFS 我们会采用递归的方式实现(当然你强行写一个非递归的版本也是可以的),而 BFS 则无需递归(使用队列 Queue + 哈希表 HashMap就可以)。所以我们在面试中,如果一个问题既可以使用 DFS,又可以使用 BFS 的情况下,一定要优先使用 BFS。因为他是非递归的,而且更容易实现。
什么是回溯(Backtracking)?
有的时候,深度优先搜索算法(DFS),又被称之为回溯法,所以你可以完全认为回溯法,就是深度优先搜索算法。在我的理解中,回溯实际上是深度优先搜索过程中的一个步骤。比如我们在进行全子集问题的搜索时,假如当前的集合是 {1,2} 代表我正在寻找以 {1,2}开头的所有集合。那么他的下一步,会去寻找 {1,2,3}开头的所有集合,然后当我们找完所有以 {1,2,3} 开头的集合时,我们需要把 3 从集合中删掉,回到 {1,2}。然后再把 4 放进去,寻找以 {1,2,4} 开头的所有集合。这个把 3 删掉回到 {1,2} 的过程,就是回溯。
subset.add(nums[i]);
subsetsHelper(result, subset, nums, i + 1);
subset.remove(list.size() - 1) // 这一步就是回溯
递归三要素
1. 递归的定义
每一个递归函数,都需要有明确的定义,有了正确的定义以后,才能够对递归进行拆解。
2. 递归的拆解
一个
大问题如何拆解为若干个小问题去解决。
3. 递归的出口
什么时候可以直接知道答案,不用再拆解,直接 return
使用 ResultType 返回多个值
什么是 ResultType
通常是我们定义在某个文件内部使用的一个类。比如:
class ResultType {
int maxValue, minValue;
ResultType(int maxValue, int minValue) {
this.maxValue = maxValue;
this.minValue = minValue;
}
};
什么时候需要 ResultType
当我们定义的函数需要返回多个值供调用者计算时,就需要使用 ResultType了。
所以如果你只是返回一个值就够用的话,就不需要。
什么是平衡二叉树
定义
平衡二叉树(Balanced Binary Tree,又称为AVL树,有别于AVL算法)是二叉树中的一种特殊的形态。二叉树当且仅当满足如下两个条件之一,是平衡二叉树:
- 空树。
- 左右子树高度差绝对值不超过1且左右子树都是平衡二叉树。
AVL树的高度为 O(logN)
AVL树有什么用?
若二叉搜索树是AVL树,则最大作用是保证查找的最坏时间复杂度为O(logN)。而且较浅的树对插入和删除等操作也更快。
AVL树必定是二叉搜索树,反之则不一定。
Set/Map
Set/Map 是底层运用了红黑树的数据结构
对比 unordered_set/unordered_map
- unordered_set/unordered_map 存取的时间复杂度为O(1),而 Set/Map 存取的时间复杂度为 O(logn) 所以在存取上并不占优。
- unordered_set/unordered_map 内元素是无序的,而Set/Map 内部是有序的(可以是按自然顺序排列也可以自定义排序)。
- unordered_set/unordered_map 还提供了类似 lowerBound 和 upperBound 这两个其他数据结构没有的方法
- 对于 Set, 实现上述两个方法的方法为:
- lowerBound
- public E lower(E e) --> 返回set中严格小于给出元素的最大元素,如果没有满足条件的元素则返回 null。
- public E floor(E e) --> 返回set中不大于给出元素的最大元素,如果没有满足条件的元素则返回 null。
- upperBound
- public E higher(E e) --> 返回set中严格大于给出元素的最小元素,如果没有满足条件的元素则返回 null。
- public E ceiling(E e) --> 返回set中不小于给出元素的最小元素,如果没有满足条件的元素则返回 null。
- lowerBound
- 对于 Map , 实现上述两个方法的方法为:
- lowerBound
- public Map.Entry<K,V> lowerEntry(K key) --> 返回map中严格小于给出的key值的最大key对应的key-value对,如果没有满足条件的key则返回 null。
- public K lowerKey(K key) --> 返回map中严格小于给出的key值的最大key,如果没有满足条件的key则返回 null。
- public Map.Entry<K,V> floorEntry(K key) --> 返回map中不大于给出的key值的最大key对应的key-value对,如果没有满足条件的key则返回 null。
- public K floorKey(K key) --> 返回map中不大于给出的key值的最大key,如果没有满足条件的key则返回 null。
- upperBound
- public Map.Entry<K,V> higherEntry(K key) --> 返回map中严格大于给出的key值的最小key对应的key-value对,如果没有满足条件的key则返回 null。
- public K higherKey(K key) --> 返回map中严格大于给出的key值的最小key,如果没有满足条件的key则返回 null。
- public Map.Entry<K,V> ceilingEntry(K key) --> 返回map中不小于给出的key值的最小key对应的key-value对,如果没有满足条件的key则返回 null。
- public K ceilingKey(K key) --> 返回map中不小于给出的key值的最小key,如果没有满足条件的key则返回 null。
- lowerBound
- lowerBound 与 upperBound 均为二分查找(因此要求有序),时间复杂度为O(logn).
- 对于 Set, 实现上述两个方法的方法为:
对比 priority_queue(Heap)
priority_queue是基于Heap实现的,它可以保证队头元素是优先级最高的元素,但其余元素是不保证有序的。
Heap 是完全二叉树
- 方法时间复杂度对比:
- 添加元素 add() / offer()
- Set: O(logn)
- priority_queue: O(logn)
- 删除元素 poll() / remove()
- Set: O(logn)
- priority_queue: O(logn)
- 查找 contains()
- Set: O(logn)
- priority_queue: O(n)
- 取最小值 first() / peek()
- Set: O(logn)
- priority_queue: O(1)
- 添加元素 add() / offer()
什么是二叉搜索树
定义
二叉搜索树(Binary Search Tree,又名排序二叉树,二叉查找树,通常简写为BST)定义如下:
空树或是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有节点值均小于或等于它的根节点值;
(2)若右子树不空,则右子树上所有节点值均大于或等于它的根节点值;
(3)左、右子树也为二叉搜索树;
BST 的特性
- 按照中序遍历(inorder traversal)打印各节点,会得到由小到大的顺序。
- 在BST中搜索某值的平均时间复杂度为O(logN),其中N为节点个数。类似binary search,将待寻值与节点值比较,若不相等,则通过是小于还是大于,可断定该值只可能在左子树还是右子树,继续向该子树搜索。故一次比较平均排除半棵树。
BST 的作用
- 通过中序遍历,可快速得到升序节点列表。
- 在BST中查找元素,只需要平均O(logN)的时间,这与有序数组(sorted array)一样。但BST平均log(N)即可实现元素的增加和删除,有序数组却需要O(N)。
BST基本操作——增删改查(CRUD)
基本操作之查找(Retrieve)
-
思路
- 查找值为val的节点,如果val小于根节点则在左子树中查找,反之在右子树中查找
基本操作之修改(Update)
-
思路
- 修改仅仅需要在查找到需要修改的节点之后,更新这个节点的值就可以了
基本操作之增加(Create)
-
思路
- 根节点为空,则待添加的节点为根节点
- 如果待添加的节点值小于根节点,则在左子树中添加
- 如果待添加的节点值大于根节点,则在右子树中添加
- 我们统一在树的叶子节点(Leaf Node)后添加
基本操作之删除(Delete)
-
思路(最为复杂)
- 考虑待删除的节点为叶子节点,可以直接删除并修改父亲节点(Parent Node)的指针,需要区分待删节点是否为根节点
- 考虑待删除的节点为单支节点(只有一棵子树——左子树 or 右子树),与删除链表节点操作类似,同样的需要区分待删节点是否为根节点
- 考虑待删节点有两棵子树,可以将待删节点与左子树中的最大节点进行交换,由于左子树中的最大节点一定为叶子节点,所以这时再删除待删的节点可以参考第一条
用 Morris 算法实现 O(1) 额外空间遍历二叉树
什么是 Morris 算法
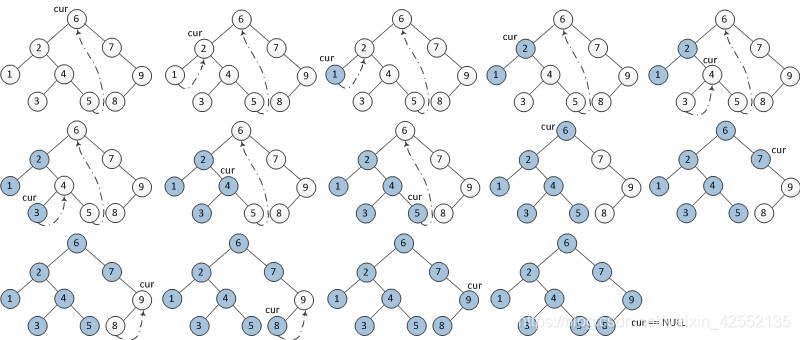
与递归和使用栈空间遍历的思想不同,Morris 算法使用二叉树中的叶节点的right指针来保存后面将要访问的节点的信息,当这个right指针使用完成之后,再将它置为null,但是在访问过程中有些节点会访问两次,所以与递归的空间换时间的思路不同,Morris则是使用时间换空间的思想。
class TreeNode{
int val;
TreeNode left;
TreeNode right;
pubic TreeNode(int val) {
this.val = val;
this.left = this.right = null;
}
}1. 如果当前节点的左孩子为空,则输出当前节点并将其右孩子作为当前节点。
2. 如果当前节点的左孩子不为空,在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。
1. 如果前驱节点的右孩子为空,将它的右孩子设置为当前节点。当前节点更新为当前节点的左孩子。
2. 如果前驱节点的右孩子为当前节点,将它的右孩子重新设为空(恢复树的形状)。输出当前节点。当前节点更新为当前节点的右孩子。
3. 重复1、2两步直到当前节点为空。public class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> nums = new ArrayList<>();
TreeNode cur = null;
while (root != null) {
if (root.left != null) {
cur = root.left;
while (cur.right != null && cur.right != root) {
cur = cur.right;
}
if (cur.right == root) {
nums.add(root.val);
cur.right = null;
root = root.right;
} else {
cur.right = root;
root = root.left;
}
} else {
nums.add(root.val);
root = root.right;
}
}
return nums;
}
}非递归的方式实现二叉树遍历
先序遍历
思路
遍历顺序为根、左、右
- 如果根节点非空,将根节点加入到栈中。
- 如果栈不空,弹出出栈顶节点,将其值加加入到数组中。
- 如果该节点的右子树不为空,将右子节点加入栈中。
- 如果左子节点不为空,将左子节点加入栈中。
- 重复第二步,直到栈空。
中序遍历
思路
遍历顺序为左、根、右
- 如果根节点非空,将根节点加入到栈中。
- 如果栈不空,取栈顶元素(暂时不弹出),
- 如果左子树已访问过,或者左子树为空,则弹出栈顶节点,将其值加入数组,如有右子树,将右子节点加入栈中。
- 如果左子树不为空,则将左子节点加入栈中。
- 重复第二步,直到栈空。
后序遍历
思路
遍历顺序为左、右、根
- 如果根节点非空,将根节点加入到栈中。
- 如果栈不空,取栈顶元素(暂时不弹出),
- 如果(左子树已访问过或者左子树为空),且(右子树已访问过或右子树为空),则弹出栈顶节点,将其值加入数组,
- 如果左子树不为空,切未访问过,则将左子节点加入栈中,并标左子树已访问过。
- 如果右子树不为空,切未访问过,则将右子节点加入栈中,并标右子树已访问过。
- 重复第二步,直到栈空。





















 313
313

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








