python深度优先非递归_小张学算法之基础算法：6.树的广度优先遍历和深度优先遍历(非递归python)...

广度优先遍历

思想：使用队列，每一层，先将自己遍历后，在将孩子进队列，左先右后。

def broad_travel(self, root, func):

queue = [root]

while queue:

node = queue.pop(0)

func(node.data)

if node.lchild:

queue.append(node.lchild)

if node.rchild:

queue.append(node.rchild)

深度优先遍历(非递归)

思想采用栈来保存先驱节点。

线序中序侯旭分开做。先序即遍历时第一次经过是就处理，中序是第二次，后续是第三次。

先序遍历：

思想：一直沿着树向左走，遍历自己的时候，同时将左右字节点入栈，由于栈是先入后出的，所以，要先压右孩子再压左孩子，初始值先将root节点入栈。

def deep_travel_first(self, root, func):

stack = [root]

last_pop=None

while stack:

node = stack.pop() #last item

func(node.data)

if node.rchild :

stack.append(node.rchild)

if node.lchild :

stack.append(node.lchild)

中序遍历

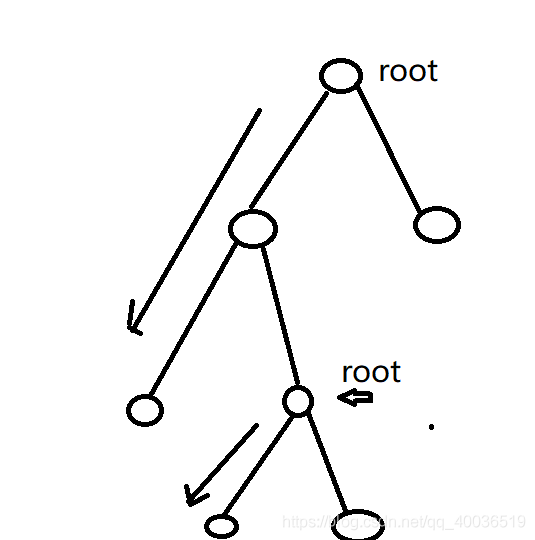
思想：一直沿着树向左走，如果左孩子为空，则pop自己，处理，然后将右孩子作为根节点，然后再继续向左走。

def deep_travel_middle(self, root, func):

stack = []

last_pop=None

while stack or root:

while root:

stack.append(root)

root = root.lchild

if stack:

node = stack.pop()

func(node.data)

root = node.rchild

后序遍历

思想： 后续遍历，顺序是：左右中，但是我们遍历都是从中间走向孩子节点，没法分开左右，解决办法：可以走中右中左的顺序，但是在第二次经过中的时候不做处理，然后，利用栈的属性，将其顺序逆置，得到左右中，一直向右走，然后走不动时，将左孩子设置为root，然后继续往右走。

def deep_travel_final(self, root, func):

stack = []

last_pop=None

result=[]

while stack or root:

while root:

stack.append(root)

result.append(root.data)

root = root.rchild

if stack:

node = stack.pop()

root = node.lchild

result=result[::-1] #reverse middle->right->left to left->right->middle

for dat in result:

func(dat)

整个代码：

class bNode:

def __init__(self, dat):

self.data = dat

self.lchild = None

self.rchild = None

class bTree:

def __init__(self):

self.root = None

# from left to right to insert

def insert(self, node):

if self.root == None:

self.root = node

return

cur_node = self.root #board travel

queue = [cur_node]

while queue :

node_itr = queue.pop(0)

if node_itr.lchild:

queue.append(node_itr.lchild)

else:

node_itr.lchild = node

return

if node_itr.rchild:

queue.append(node_itr.lchild)

else:

node_itr.rchild = node

return

def first_travel(self, root, func):

if not root:

return

if func:

func(root.data)

self.first_travel(root.lchild, func)

self.first_travel(root.rchild, func)

def middle_travel(self, root, func):

if not root:

return

self.middle_travel(root.lchild, func)

if func:

func(root.data)

self.middle_travel(root.rchild, func)

def last_travel(self, root, func):

if not root:

return

self.last_travel(root.lchild, func)

self.last_travel(root.rchild, func)

if func:

func(root.data)

def broad_travel(self, root, func):

queue = [root]

while queue:

node = queue.pop(0)

func(node.data)

if node.lchild:

queue.append(node.lchild)

if node.rchild:

queue.append(node.rchild)

def deep_travel_first(self, root, func):

stack = [root]

last_pop=None

while stack:

node = stack.pop() #last item

func(node.data)

if node.rchild :

stack.append(node.rchild)

if node.lchild :

stack.append(node.lchild)

def deep_travel_middle(self, root, func):

stack = []

last_pop=None

while stack or root:

while root:

stack.append(root)

root = root.lchild

if stack:

node = stack.pop()

func(node.data)

root = node.rchild

def deep_travel_final(self, root, func):

stack = []

last_pop=None

result=[]

while stack or root:

while root:

stack.append(root)

result.append(root.data)

root = root.rchild

if stack:

node = stack.pop()

root = node.lchild

result=result[::-1] #reverse middle->right->left to left->right->middle

for dat in result:

func(dat)

def printf(data):

print("%d " % data)

root_tree = bTree()

root_tree.insert(bNode(8))

root_tree.insert(bNode(10))

root_tree.insert(bNode(12))

root_tree.insert(bNode(0))

root_tree.insert(bNode(100))

root_tree.insert(bNode(101))

print("first_travel:")

root_tree.first_travel(root_tree.root, printf)

print("middle_travel:")

root_tree.middle_travel(root_tree.root, printf)

print("last_travel:")

root_tree.last_travel(root_tree.root, printf)

print("broad_travel:")

root_tree.broad_travel(root_tree.root, printf)

print("deep_travel_first:")

root_tree.deep_travel_first(root_tree.root, printf)

print("deep_travel_middle:")

root_tree.deep_travel_middle(root_tree.root, printf)

print("deep_travel_final:")

root_tree.deep_travel_final(root_tree.root, printf)

if __name__ == "__main__":

main()

原文链接:https://blog.youkuaiyun.com/qq_40036519/article/details/107136059