什么是机器学习
机器学习就是从数据中自动分析获得模型,并利用模型对未知数据进行预测。
数据集的构成
特征值+目标值
机器学习算法分类
监督学习:
目标值:类别–分类问题 K-近邻算法、贝叶斯算法、决策树与随机森林、逻辑回归
目标值:连续型的数据–回归问题 线性回归、岭回归
无监督学习:
目标值:无 聚类 K-means
机器学习开发流程
1)获取数据
2)数据处理
3)特征工程
4)机器学习算法训练 —— 模型
5)模型评估
6)应用
机器学习算法
KNN算法
K近邻算法,当需要表示一个样本的值的时候,就使用与该样本最接近的K个邻居来决定。KNN既可以用于分类,也可以用于回归。
过程:
1.从训练集中选择离待预测样本最近的K个样本
2.根据这k个样本计算待预测样本的值(属于哪个类别或者一个具体的数值)
KNN分类
import numpy as np
import pandas as pd
#读取鸢尾花数据集,header参数来指定标题的行,默认为0,如果没有标题,则使用None
data = pd.read_csv(r"iris_training.csv")
#print(data)
#显示前n行记录,默认n为5
#print(data.head())
#显示末尾的n行记录,默认n为5
#print(data.tail())
#随机抽取n条记录,默认n为1
#print(data.sample())
class KNN:
def __init__(self,k):
#k邻居个数
self.k = k
def fit(self,X,y):
#训练方法
#将X转换成ndarray数组类型
self.X = np.asarray(X)
self.y = np.asarray(y)
def predict(self,X):
#根据参数传递的样本,对样本数据进行预测
X = np.asarray(X)
result = []
#对ndarray数组进行遍历,每次取数组中的一行
for x in X:
#对于测试集中的每一个样本,依次与训练集中的所有样本求距离 欧氏距离
dis = np.sqrt(np.sum((x - self.X) ** 2,axis = 1))
#返回数组排序后,每个元素在原数组中的索引
index = dis.argsort()
#进行截断,只取前k个元素[取距离最近的k个元素的索引]
index = index[:self.k]
#返回数组中每个元素出现的次数,元素必须是非负的整数
count = np.bincount(self.y[index])
#返回ndarray数组中,值最大的元素对应的索引,该索引就是我们判定的类别
#最大元素索引,就是出现次数最多的元素
result.append(count.argmax())
return np.asarray(result)
#考虑权重,使用距离的倒数作为权重
def predict1(self,X):
#根据参数传递的样本,对样本数据进行预测
X = np.asarray(X)
result = []
#对ndarray数组进行遍历,每次取数组中的一行
for x in X:
#对于测试集中的每一个样本,依次与训练集中的所有样本求距离 欧氏距离
dis = np.sqrt(np.sum((x - self.X) ** 2,axis = 1))
#返回数组排序后,每个元素在原数组中的索引
index = dis.argsort()
#进行截断,只取前k个元素[取距离最近的k个元素的索引]
index = index[:self.k]
#返回数组中每个元素出现的次数,元素必须是非负的整数,[使用weights考虑权重,权重为距离的倒数]
count = np.bincount(self.y[index],weights = 1/dis[index])
#返回ndarray数组中,值最大的元素对应的索引,该索引就是我们判定的类别
#最大元素索引,就是出现次数最多的元素
result.append(count.argmax())
return np.asarray(result)
#提取出每个类别的鸢尾花数据
t0 = data[data["Species"]==0]
t1 = data[data["Species"]==1]
t2 = data[data["Species"]==2]
#对每个类别数据进行洗牌
t0 = t0.sample(len(t0),random_state=0)
t1 = t1.sample(len(t1),random_state=0)
t2 = t2.sample(len(t2),random_state=0)
#构建训练集与测试集
train_X = pd.concat([t0.iloc[:30,:-1],t1.iloc[:30,:-1],t2.iloc[:30,:-1]],axis=0)
train_y = pd.concat([t0.iloc[:30,-1],t1.iloc[:30,-1],t2.iloc[:30,-1]],axis=0)
test_X = pd.concat([t0.iloc[30:,:-1],t1.iloc[30:,:-1],t2.iloc[30:,:-1]],axis=0)
test_y = pd.concat([t0.iloc[30:,-1],t1.iloc[30:,-1],t2.iloc[30:,-1]],axis=0)
#创建KNN对象,进行训练与测试
knn = KNN(k = 4)
#进行训练
knn.fit(train_X,train_y)
#进行测试,获得测试结果
#result = knn.predict(test_X)
result = knn.predict1(test_X) #对于距离不均匀,差距很大的,可能会产生很大变化
# print(result)
# print(test_y)
print(np.sum(result == test_y))
print(len(result))
print(np.sum(result == test_y)/len(result))
import matplotlib as mpl
import matplotlib.pyplot as plt
#设置字体为黑体,以支持中文显示
mpl.rcParams["font.family"] = "SimHei"
#设置在中文字体时,可以正常显示负号
mpl.rcParams["axes.unicode_minus"] = False
plt.figure(figsize=(10,10))
#绘制训练集数据
plt.scatter(x=t0["SepalLength"][:30],y=t0["PetalLength"][:30],color ="r")
plt.scatter(x=t1["SepalLength"][:30],y=t1["PetalLength"][:30],color ="g")
plt.scatter(x=t2["SepalLength"][:30],y=t2["PetalLength"][:30],color ="b")
#绘制测试集数据
right = test_X[result == test_y]
wrong = test_X[result != test_y]
plt.scatter(x=right["SepalLength"],y=right["PetalLength"],color="c",marker="x")
plt.scatter(x=wrong["SepalLength"],y=wrong["PetalLength"],color="m",marker=">")
plt.xlabel("花萼长度")
plt.ylabel("花瓣长度")
plt.title("KNN分类结果显示")
plt.show()
KNN回归
import numpy as np
import pandas as pd
#读取鸢尾花数据集,header参数来指定标题的行,默认为0,如果没有标题,则使用None
data = pd.read_csv(r"iris.csv")
class KNN:
# 根据前三个特征属性,寻找最近的K个邻居,然后根据k个邻居的第四个特征属性,去预测当前样本的第四个特征值
def __init__(self,k):
self.k = k
def fit(self,X,y):
"""训练方法
X:类数组类型(矩阵类型)。形状为【样本数量,特征数量】
待训练的样本特征(属性)
y:类数组类型(目标标签)。形状为【样本数量】
每个样本的目标值(标签)
"""
#将X,y转换成ndarray数组的形式,方便统一进行操作
self.X = np.asarray(X)
self.y = np.asarray(y)
def predict(self,X):
"""
根据参数传递的X,对样本数据进行预测
:param X: 类数组类型(矩阵类型)。形状为【样本数量,特征数量】
待预测的样本特征(属性)
:return: result:数组类型。预测的结果值
"""
#转换成数组类型
X = np.asarray(X)
#保存预测的结果值
result = []
for x in X:
#计算距离。计算与训练集中的每个X个距离
dis = np.sqrt(np.sum((x-self.X) ** 2,axis=1))
#返回数组排序后,每个元素在原数组中(排序之前的数组)的索引
index = dis.argsort()
#取前k个距离最近的索引(在原数组中的索引)
index = index[:self.k]
#计算均值加入返回的结果列表中
result.append(np.mean(self.y[index]))
return np.array(result)
def predict1(self,X):
"""
根据参数传递的X,对样本数据进行预测(考虑权重)
权重的计算方法:使用每个节点(邻居)距离的倒数/所有节点距离倒数之和
:param X: 类数组类型(矩阵类型)。形状为【样本数量,特征数量】
待预测的样本特征(属性)
:return: result:数组类型。预测的结果值
"""
#转换成数组类型
X = np.asarray(X)
#保存预测的结果值
result = []
for x in X:
#计算距离。计算与训练集中的每个X个距离
dis = np.sqrt(np.sum((x-self.X) ** 2,axis=1))
#返回数组排序后,每个元素在原数组中(排序之前的数组)的索引
index = dis.argsort()
#取前k个距离最近的索引(在原数组中的索引)
index = index[:self.k]
#计算所有邻居节点距离的倒数之和【注意:最后加上一个很小的值,就是为了避免除数距离为0的情况】
s = np.sum(1/(dis[index]+0.001))
#使用每一个节点距离的倒数,除以倒数之和,得到权重
weight = (1/(dis[index]+0.001))/s
#使用邻居节点的标签值乘以对应的权重,然后相加得到最终的预测结果
result.append(np.sum(self.y[index] * weight))
return np.array(result)
t = data.sample(len(data),random_state=0)
train_X = t.iloc[:120,:-2]
train_y = t.iloc[:120,-2]
test_X = t.iloc[120:,:-2]
test_y = t.iloc[120:,-2]
knn = KNN(k=1)
knn.fit(train_X,train_y)
#result = knn.predict(test_X)
result = knn.predict1(test_X)
print(result)
print(np.mean((result-test_y)**2))
print(test_y.values)
import matplotlib as mpl
import matplotlib.pyplot as plt
#设置字体为黑体,以支持中文显示
mpl.rcParams["font.family"] = "SimHei"
#设置在中文字体时,可以正常显示负号
mpl.rcParams["axes.unicode_minus"] = False
plt.figure(figsize=(10,10))
#绘制预测值
plt.plot(result,"ro-",label="预测值")
#绘制真实值
plt.plot(test_y.values,"go--",label="真实值")
plt.title("KNN连续值预测展示")
plt.xlabel("节点序号")
plt.ylabel("花瓣宽度")
plt.legend()
plt.show()
线性回归
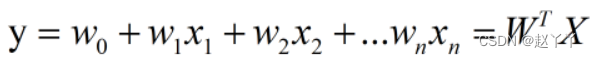
线性回归的目标函数:
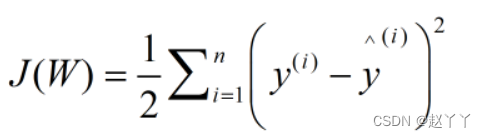
采用两种方式进行求解:
1、最小二乘法
不考虑截距
import numpy as np
import pandas as pd
data = pd.read_csv(r"boston.csv")
#print(data)
#查看数据的基本信息,同时,也可以用来查看,各个特征值是否存在缺省值
#print(data.info())
#查看是否存在重复值
#print(data.duplicated().any())
class LinearRegression:
def fit(self,X,y):
"""
#根据提供的训练数据X,对模型进行训练
:param X: 类数组类型。形状为【样本数量,特征数量】
特征矩阵,用来对模型进行训练
:param y: 类数组类型。形状为【样本数量】
"""
#说明:如果X是数组对象的一部分,而不是完整的对象数据(例如:X是由其他对象通过切片传递过来)
#则无法完成矩阵的转换
#这里创建X的拷贝对象,避免转换矩阵的时候失败
X = np.asmatrix(X.copy())
# y是一维数据(行向量或列向量),一维结构可以不用进行拷贝
# 注意:进行矩阵的运算,需要二维结构,所以通过reshape方法进行转换
y = np.asmatrix(y).reshape(-1,1)
#通过最小二乘公式,求解出最佳的权重值
self.w_ = (X.T * X).I * X.T * y
def predict(self,X):
"""
#根据参数传递的样本X,对样本数据进行预测
:param X:类数组类型。形状为【样本数量,特征数量】
待预测的样本特征(属性)
:return:数组类型,预测结果。
"""
#将X转换成矩阵,注意,需要对X进行拷贝
X = np.asmatrix(X.copy())
result = X * self.w_
#将矩阵转换成ndarray数组,进行扁平化处理,然后返回结果
return np.array(result).ravel()
#不考虑截距
# t = data.sample(len(data),random_state=0)
# train_X = t.iloc[:400,:-1]
# train_y = t.iloc[:400,-1]
# test_X = t.iloc[400:,:-1]
# test_y = t.iloc[400:,-1]
#
# lr = LinearRegression()
# lr.fit(train_X, train_y)
# result = lr.predict(test_X)
# #print(result)
# print(np.mean((result-test_y)**2))
#
# #查看模型的权重值
# print(lr.w_)
考虑截距
#考虑截距,增加一列,该列的所有值都是1
t = data.sample(len(data),random_state=0)
#print(t)
#截距作为w0,为之配上一个x0,x0列放到最前面
new_colums = t.columns.insert(0,"Intercept")
#重新安排列的顺序,如果值为空,则使用fill_value值指定的参数进行填充
t = t.reindex(columns=new_colums,fill_value=1)
train_X = t.iloc[:400,:-1]
train_y = t.iloc[:400,-1]
test_X = t.iloc[400:,:-1]
test_y = t.iloc[400:,-1]
lr = LinearRegression()
lr.fit(train_X, train_y)
result = lr.predict(test_X)
#print(result)
print(np.mean((result-test_y)**2))
print(lr.w_)
import matplotlib as mpl
import matplotlib.pyplot as plt
#设置字体为黑体,以支持中文显示
mpl.rcParams["font.family"] = "SimHei"
#设置在中文字体时,可以正常显示负号
mpl.rcParams["axes.unicode_minus"] = False
plt.figure(figsize=(10,10))
#绘制预测值
plt.plot(result,"ro-",label="预测值")
#绘制真实值
plt.plot(test_y.values,"go--",label="真实值")
plt.title("线性回归预测-最小二乘法")
plt.xlabel("样本序号")
plt.ylabel("房价")
plt.legend()
plt.show()
2、梯度下降法
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
data = pd.read_csv(r"boston.csv")
class LinearRegression:
def __init__(self,alpha,times):
"""
#初始化方法
:param alpha: float 学习率,用来控制步长(权重调整的幅度)
:param times: 循环迭代的次数
"""
self.alpha = alpha
self.times = times
def fit(self,X,y):
"""
#根据提供的训练数据X,对模型进行训练
:param X: 类数组类型。形状为【样本数量,特征数量】
特征矩阵,用来对模型进行训练
:param y: 类数组类型。形状为【样本数量】
目标值(标签信息)
"""
X = np.asarray(X)
y = np.asarray(y)
#创建权重的向量,初始值为0(或任何其他的值),一维的形式,长度比特征数量多1(多出的一个值就是截距)
self.w_ = np.zeros(1 + X.shape[1])#索引为0是样本数量的值,索引为1是特征数量的值
#创建损失列表,用来保存每次迭代后的损失值,损失值计算:(预测值-真实值)的平方除以2
self.loss_ = []
#进行循环,多次迭代,在每次迭代的过程中,不断的去调整权重值,使得损失值不断减小
for i in range(self.times):
y_hat = np.dot(X,self.w_[1:]) + self.w_[0]
#计算真实值与预测值之间的差距
error = y - y_hat
#将损失值加入到损失列表当中
self.loss_.append(np.sum(error ** 2) /2)
#根据差距调整群众w_,根据公式:权重(j) = 权重(j) + 学习率 * sum((y - y_hat) * x(j))
self.w_[0] += self.alpha * np.sum(error)
self.w_[1:] += self.alpha * np.dot(X.T,error)
def predict(self,X):
"""
根据参数传递的样本,对样本数据进行预测
:param X: 类数组类型,形状[样本数量,特征数量]
待测试的样本
:return: result:数组类型 预测的结果
"""
X = np.asarray(X)
result = np.dot(X,self.w_[1:]) + self.w_[0]
return result
# lr = LinearRegression(alpha=0.0005,times=20)
# t = data.sample(len(data),random_state=0)
# train_X = t.iloc[:400,:-1]
# train_y = t.iloc[:400,-1]
# test_X = t.iloc[400:,:-1]
# test_y = t.iloc[400:,-1]
#
# lr.fit(train_X, train_y)
# result = lr.predict(test_X)
#
# print(np.mean((result-test_y)**2)) #误差值
# print(lr.w_)
# print(lr.loss_)
标准化处理
class StandarScaler:
"""
对数据进行标准化处理 标准的正态分布形式,均值为0,标准差为1
"""
def fit(self, X):
"""
根据传递的样本,计算每个特征列的均值和标准差
:param X:类数组类型,训练数据,用来计算均值与标准差
:return:
"""
X = np.asarray(X)
self.std_ = np.std(X, axis=0) # 标准差
self.mean_ = np.mean(X, axis=0) # 平均数
def transform(self, X):
"""
对给定的数据X进行标准化处理(将X的每一列都变成标准正态分布的数据)
:param X: 类数组类型,待转换的数据
:return: 参数X转换成标准正态分布的结果
"""
return (X - self.mean_) / self.std_
def fit_transform(self, X):
"""
对数据进行训练,并转换,返回转换后的结果
:param X: 类数组类型,待转换的数据
:return: 参数X转换成标准正态分布的结果
"""
self.fit(X)
return self.transform(X)
# #为了避免每个特征数量集的不同,从而在梯度下降的过程中带来影响,考虑对每个特征进行标准化处理
# lr = LinearRegression(alpha=0.0005,times=20)
# t = data.sample(len(data),random_state=0)
# train_X = t.iloc[:400,:-1]
# train_y = t.iloc[:400,-1]
# test_X = t.iloc[400:,:-1]
# test_y = t.iloc[400:,-1]
#
# #对数据集进行标准化的处理
# s = StandarScaler()
# train_X = s.fit_transform(train_X)
# #print(train_X)
# test_X = s.transform(test_X)
# s1 = StandarScaler()
# train_y = s1.fit_transform(train_y)
# test_y = s1.transform(test_y)
# lr.fit(train_X,train_y)
# result = lr.predict(test_X)
# print(np.mean((result-test_y)**2))
# print(lr.w_)
# print(lr.loss_)#损失值随着迭代不断下降
绘制测试集的真实值与预测值
# import matplotlib as mpl
# import matplotlib.pyplot as plt
# #设置字体为黑体,以支持中文显示
# mpl.rcParams["font.family"] = "SimHei"
# #设置在中文字体时,可以正常显示负号
# mpl.rcParams["axes.unicode_minus"] = False
#
# plt.figure(figsize=(10,10))
#
# #绘制预测值
# plt.plot(result,"ro-",label="预测值")
# #绘制真实值
# plt.plot(test_y.values,"go--",label="真实值")
# plt.title("线性回归预测-梯度下降法")
# plt.xlabel("样本序号")
# plt.ylabel("房价")
# plt.legend()
# plt.show()
#
# #绘制累计误差值
# plt.plot(range(1,lr.times + 1),lr.loss_,"o-")
# plt.show()
绘制直线拟合
#房价涉及多个维度,只选取一个维度进行可视化,实现拟合
lr = LinearRegression(alpha=0.0005,times=20)
t = data.sample(len(data),random_state=0)
train_X = t.iloc[:400,5:6]
train_y = t.iloc[:400,-1]
test_X = t.iloc[400:,5:6]
test_y = t.iloc[400:,-1]
#对数据集进行标准化的处理
s = StandarScaler()
train_X = s.fit_transform(train_X)
#print(train_X)
test_X = s.transform(test_X)
s1 = StandarScaler()
train_y = s1.fit_transform(train_y)
test_y = s1.transform(test_y)
lr.fit(train_X,train_y)
result = lr.predict(test_X)
print(np.mean((result-test_y)**2))
plt.scatter(train_X["RM"],train_y)
#查看方程系数
print(lr.w_)
#构建方程
x = np.arange(-5,5,0.1)
y = -2.58681965e-16 + 6.47442390e-01 * x
#plt.plot(x,y,"r")
plt.plot(x,lr.predict(x.reshape(-1,1)),"r")
plt.show()
逻辑回归
是一种分类模型
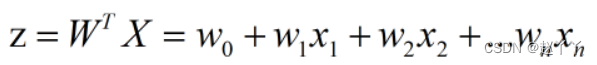
逻辑回归通过sigmoid函数将输入值
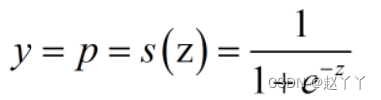
当z大于0,s(z)大于0.5,将类别判定为1
当z小于0,s(z)小于0.5,将类别判定为0
目标函数:损失函数
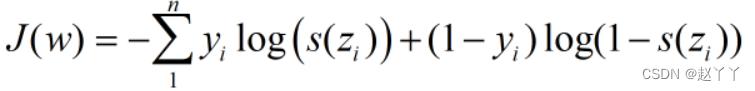
y=1,p=1,J=0
y=1,p=0,J=正无穷大
因此,目标函数最小时,w的值,就是我们要求的最终权重值
K-means聚类算法
属于无监督学习
K-means可以在数据集中分为相似的组(簇),使得组内数据的相似度较高,组间之间的相似度较低
步骤如下:
1.从样本中选择k个点作为初始簇中心
2.计算每个样本到各个簇中心的距离,将样本划分到距离最近的簇中心所对应的簇中
3.根据每个簇中的所有样本,重新计算簇中心,并更新
4.重复步骤2与3,直到簇中心的位置变化小于指定的阈值或者达到最大迭代次数为止
感知器
感知器是一种人工神经网络,其模拟生物上的神经元结构
其净输入为:
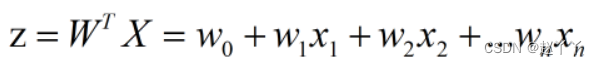
通过激活函数,就可以将其映射为1或-1
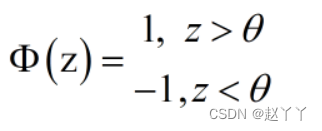




 本文介绍了机器学习,即从数据中自动分析获得模型并预测未知数据。阐述了数据集由特征值和目标值构成,对机器学习算法进行分类,包括监督学习和无监督学习。还说明了开发流程,最后详细介绍了KNN、线性回归、逻辑回归、K-means聚类算法和感知器等算法。
本文介绍了机器学习,即从数据中自动分析获得模型并预测未知数据。阐述了数据集由特征值和目标值构成,对机器学习算法进行分类,包括监督学习和无监督学习。还说明了开发流程,最后详细介绍了KNN、线性回归、逻辑回归、K-means聚类算法和感知器等算法。
















 2107
2107

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








