逻辑回归学习

逻辑回归

• 逻辑回归是解决二分类问题的利器
• 
• sigmoid函数
  -
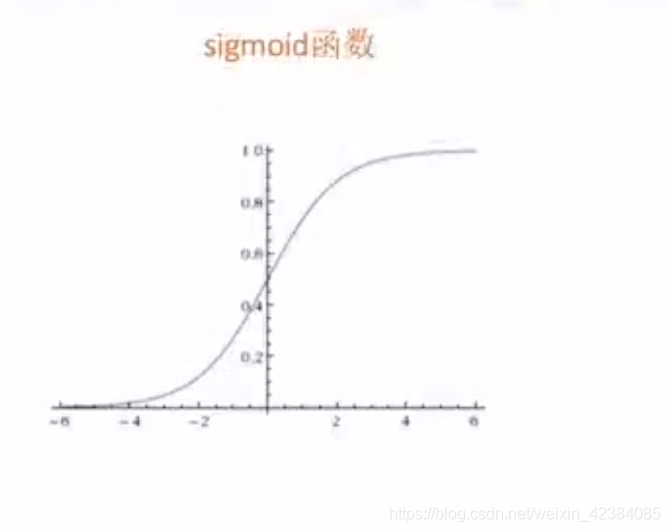
• sigmoid函数输出值[0,1]之间。
• 逻辑回归公式
• 
• Z = 回归的结果
• 逻辑回归损失函数
  -
• 
  -
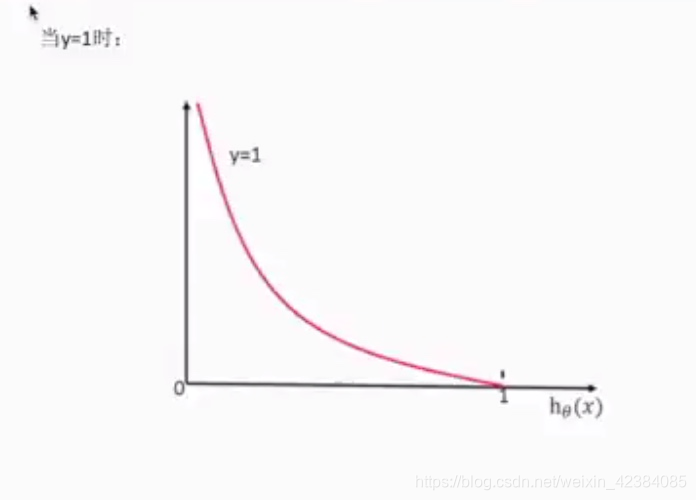
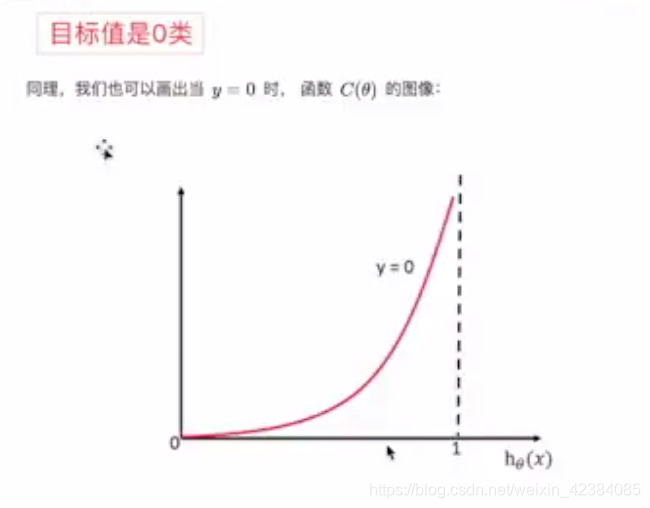
• 损失函数：
  • 均方误差（不存在多个局部最低点）只有一个最小值
  • 对数似然损失：多个局部最小值
  • 多个局部最小值解决方案：（尽量改善）
    • 1，多次随机初始化，多次比较最小值
    • 2，求解过程中，调整学习率

逻辑回归API

• sklearn.linear_model.LogisticRegression(penalty=‘l2’,C=1.0)
  • Logistic回归分类器
  • coef_:回归系数
• 逻辑回归案例：
  • 癌症预测。
  • https://archive.ics.uci.edu/ml/machine-learning-databases/
  • 1，网上获取数据（pandas）
  • 2，数据缺失值处理，标准化
  • 3，LogisticRegression估计器流程

LogisticRegression总结

• 应用：广告点击率预测、是否患病、金融诈骗、是否为虚假账号
• 优点：适合需要得到一个分类概率的场景，简单，速度快
• 缺点：不好处理多分类问题。

非监督学习

• 没有目标值，只有特征值

• k-means聚类分析

  • 1，随机在数据当中抽取k个样本，当作k个类别的中心点
  • 2，计算其余的点分别到这个中心点的距离，每一个样本有k个距离，从中选出距离最近的一个点作为自己的标记，形成k个族群
  • 3，分别计算着k个族群的平均值，把k个平均值与之前的k个旧中心点进行比较。如果相同：结束聚类；如果不相同：把k个平均值当作新的中心点，重复第二步。

• k-means的API

• sklearn.cluster.KMeans(n_clusters=8,init=‘k-means++’)

  • k-means聚类
  • n_clusters:开始的聚类中心数量
  • init：初始化方法，默认为‘k-means++’
  • labels_:默认标记类型，可以和真实值比较（不是值比较）

• kmeans性能评估指标

  • 
  • Kmeans性能评估指标API
    • sklearn.metrics.silhouette_score(X,labels)
    • 计算所有样本的平均轮廓系数
    • X：特征值
    • labels：被聚类标记的目标值

癌症预测

from sklearn.linear_model import  LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report
import pandas as pd
import numpy as np


def logistic():
    """
    逻辑回归做二分类进行癌症预测（根据细胞的属性特征）
    :return: NOne
    """
    # 构造列标签名字
    column = ['Sample code number','Clump Thickness', 'Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion', 'Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class']

    # 读取数据
    data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data", names=column)

    print(data)

    # 缺失值进行处理
    data = data.replace(to_replace='?', value=np.nan)

    data = data.dropna()

    # 进行数据的分割
    x_train, x_test, y_train, y_test = train_test_split(data[column[1:10]], data[column[10]], test_size=0.25)

    # 进行标准化处理
    std = StandardScaler()

    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test)

    # 逻辑回归预测
    lg = LogisticRegression(C=1.0)

    lg.fit(x_train, y_train)

    print(lg.coef_)

    y_predict = lg.predict(x_test)

    print("准确率：", lg.score(x_test, y_test))

    print("召回率：", classification_report(y_test, y_predict, labels=[2, 4], target_names=["良性", "恶性"]))

    return None

if __name__ == '__main__':
    logistic()