从0到1，用python实现K-NN算法

1. KNN（k-Nearest Neighbor）

k-Nearest Neighbor，即k个相对距离最小的临近点。

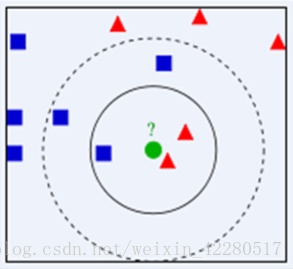
举个栗子，对于下图的这个绿色的圆来说，它到底是属于红色的三角一方，还是属于蓝色的矩形一方。面对如此虎视眈眈的两边，小圆需要立刻表明自己的立场。这次，它使用了KNN算法，它在心里盘算：

1. 就看距离我最近的这三个家伙的来历吧（取k=3），两个是红方（2/3），一个是蓝方（1/3）。嗯，我应该当红方的人。

2. 如果我看距离我最近的五个人呢（k=5），两个是红方（2/5），三个是蓝方（3/5）。嗯，我应该是蓝人。

好了，说人话

如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 KNN方法虽然从原理上也依赖于极限定理，但在类别决策时，只与极少量的相邻样本有关。

由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。 

KNN算法不仅可以用于分类，还可以用于回归。通过找出一个样本的k个最近邻居，将这些邻居的属性的平均值赋给该样本，就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight)，如权值与距离成反比。