BST树 面试题（Java）

求BST树的镜像反转

镜像的意思很明显，就是左右交换，举个例子：

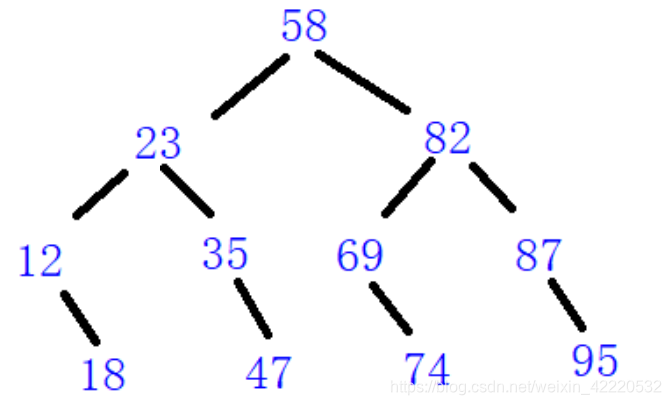
镜像后：

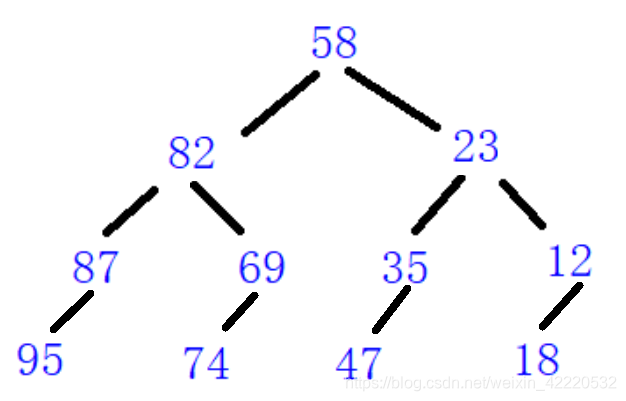
检验代码编写是否正确可以通过树的中序遍历，搜索二叉树的中序遍历是一个严格的升序，镜像后是一个严格的逆序。

思路：通过递归遍历的过程，不断的交换左右子树，直到叶子节点。这样遍历完成后，所有的左右子树都被交换了一遍，就实现了镜像。

实现代码：

public void mirror() {
    mirror(root);
}

private void mirror(BSTNode<T> root) {
    if(root != null) {
    	//交换root的左右子树
        BSTNode<T> node = root.getLeft();
        root.setLeft(root.getRight());
        root.setRight(node);
        //递归其左右子树
        mirror(root.getLeft());
        mirror(root.getRight());
    }
}

把bst树中满足[begin,end]区间的所有元素打印出来

eg:

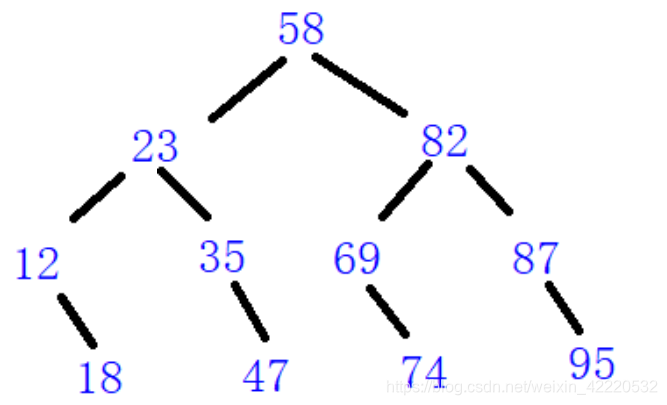
求出满足区间[10,40]的元素

那么对应这棵树，满足条件的元素是：12，18，23，35

思路：

• 看到这个问题，想想是可以套用遍历的过程的，遍历是要访问每一个节点的，我只需要判断该节点是否在范围内，如果在范围内就打印出该元素，这样遍历完整个树，就可以得到满足条件的所有元素了。
• 但是上面的思路太僵硬化，效率也不高，为什么呢?因为这是一个二叉搜索树，上面的思路只是用了二叉树的特点，确没有使用搜索这个特点：也就是左子树所有比该当前节点小，右子树所有的节点比当前节点大。
  要利用这个特性，就可以少去很多递归，首先需要判断当前节点root和该区间的关系，可以把关系分为三种，画图来理解：
  
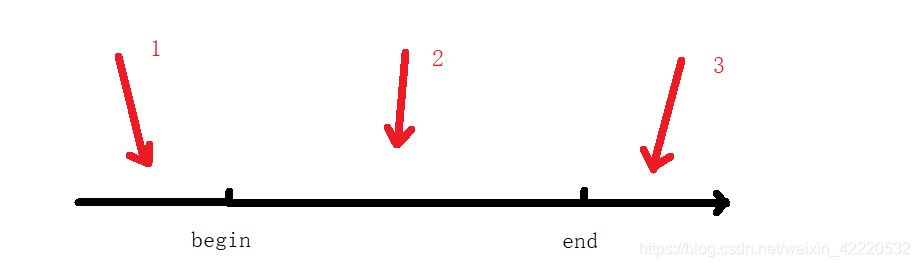
  1.begin>root,那么就要去root的右子树去找
  2.begin<=root<=end,那么当前root就在该区间中，先打印root，然后根据root把区间分为两部分递归
  3.root>end,那么就要去root的左子树去找

第一种思路就是普通的遍历，这里只给出第二种思路的代码

public void printAreaDatas(T begin,T end) {
    printAreaDatas(root,begin,end);
}

private void printAreaDatas(BSTNode<T> root, T begin, T end) {
	//遍历到叶子节点返回
	if(root == null){
         return;
    }
    
    // 只有当前节点的值大于begin的时候，才去递归root的左子树
    //如果小于，就不用递归了，减少了递归的次数
    if(root.getData().compareTo(begin) > 0){
        printAreaDatas(root.getLeft(), begin, end);
    }

    //如果root在范围内，就打印当前root节点的数据
    if(root.getData().compareTo(begin) >= 0
    && root.getData().compareTo(end) <= 0){
        System.out.print(root.getData() + " ");
    }

    // 当前节点的值小于end，才有必要继续访问当前节点的右子树
    if(root.getData().compareTo(end) < 0){
        printAreaDatas(root.getRight(), begin, end);
    }

判断一个二叉树是否是BST树（阿里）

给出根节点root，判断该树是否是一棵BST树。

有一种错误的思路：递归每一个节点，判断左孩子是否比该节点小，右孩子是否比该节点大，如果每一个节点都满足条件，那么就是一棵BST树。
这种思路是错误的，这里给出一个逻辑漏洞，看图：

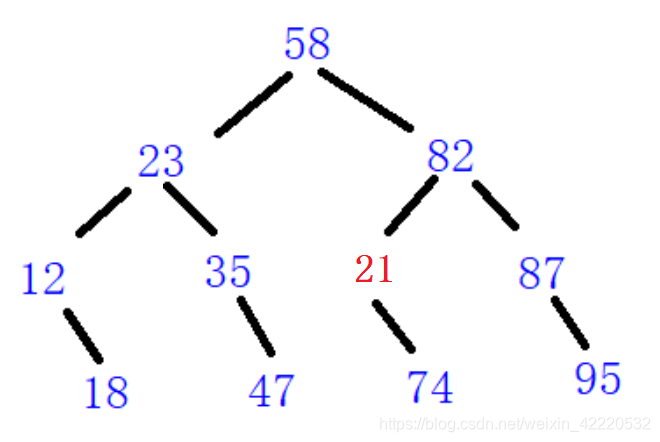
这里的21是错误的，右孩子74比21大，21比82小，满足条件，但不是一棵BST树，所以这种思路是错误的。

思路：BST树的中序遍历是一个严格递增的序列，如果有任何位置出现问题，那么就不满足严格递增，所以从严格递增入手，利用中序遍历当前的节点与上一个遍历的节点进行比较，如果不是递增就返回false

先定义一个成员变量value，用value来保存上一个中序遍历的节点数据

    T value;

注意：为什么要定义成员变量而不是通过参数递归进去呢？
public boolean isBST(BSTNode root,T value)
因为在递归回退的过程中是记忆不了数据的，举个例子：

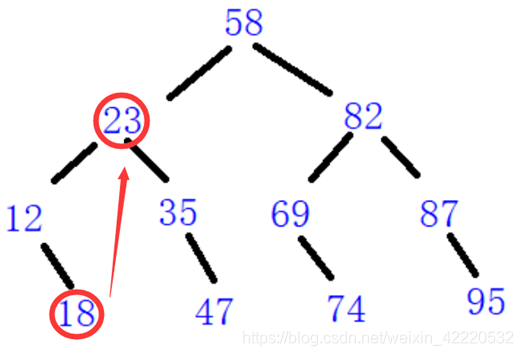
在中序遍历从18回到23的时候，虽然在递归过程中设置了当前value是18，但是回溯过程并不会知道23的上一个节点是18，而是默认在递进过程中的null

代码：

	public boolean isBST() {
        return isBST(this.root);
    }

    private boolean isBST(BSTNode<T> root) {
        if(root == null){
            return true;
        }

        // 左子树已经不满足BST树性质了，直接返回，不用继续向下递归了
        if(!isBST(root.getLeft())){
            return false;
        }

        // root.getData  value  =>
        if(value != null && value.compareTo(root.getData()) > 0){
            return false;
        }
        // 注意当前节点判断完成后，需要更新一下value值
        value = root.getData();

        return isBST(root.getRight());
    }

返回两个节点的最近公共祖先节点

public T getLCA(T data1, T data2){

}

思路：判断当前节点和data1，data2的关系，根据所判断的关系进行递归操作。如果当前节点data在data1和data2之间，那么当前节点data肯定是最近公共祖先节点。如果不在data1和data2之间，则判断往哪一边递归即可。

代码：

	public T getLCA(T data1, T data2){
        return getLCA(this.root, data1, data2);
    }

    private T getLCA(BSTNode<T> root, T data1, T data2) {
        if(root == null){
            return null;
        }

        if(root.getData().compareTo(data1) > 0
            && root.getData().compareTo(data2) > 0){
            return getLCA(root.getLeft(), data1, data2);
        } else if(root.getData().compareTo(data1) < 0
                    && root.getData().compareTo(data2) < 0){
            return getLCA(root.getRight(), data1, data2);
        } else {
            return root.getData();
        }
    }

返回倒数第k个节点

public T getOrderValue(int k){

}

思路：这里的倒数第k个节点，是指递增序列的倒数第k个节点，这里就很自然的联想到了bst树的中序遍历，bst树的中序遍历就是一个递增序列，这时在递归时，只需要加上条件i，每递归一次，就对条件i计数，然后与k进行比较，如果相同，输出即可。

但是这里是倒数第k个节点，所以需要计算好k的值

如果递增序列是 1 2 3 4 5 6 7
要拿到倒数第2个节点，这时k=2，那么真正传入的应该是该序列的长度num 7减去k 2，然后把减得的结果传入递归参数

或者换一种思维，我中序遍历先遍历左子树，然后遍历右子树，得到的是一个递增的序列，我可以先遍历右子树，再遍历左子树，这样得到的就是一个逆序的序列。这时，直接把k传入即可。

代码：
正序找倒数第几个节点

	public T getOrderValue(int k){
		//树节点的总数
        int num = number();  
        return getOrderValue(this.root, num - k);
    }

    private int i=1;
    private T getOrderValue(BSTNode<T> root, int k) {
        if(root == null){
            return null;
        }

		//向左
        T val = getOrderValue(root.getRight(), k);
        if(val != null){
            return val;
        }
		
		//访问
        if(i++ == k)
        {
            return root.getData();
        }

		//向右
        return getOrderValue(root.getLeft(), k);
    }

逆序找正数第几个节点

	public T getOrderValue(int k){
        return getOrderValue(this.root, k);
    }
 	private int i=0;
    private T getOrderValue(BSTNode<T> root, int k) {
        if(root == null){
            return null;
        }

        T val = getOrderValue(root.getLeft(), k);
        if(val != null){
            return val;
        }

        if(i++ == k)
        {
            return root.getData();
        }

        return getOrderValue(root.getRight(), k);
    }

判断是否是子树

给定一棵树，判断该树是否是当前树的子树

public boolean isChildTree(BST<T> tree){

}

思路：判断是否是子树，肯定要同时比较当前树和给定树的每一个节点，所以递归函数应该对这两棵树同时递归，要往左都往左走，要往右走同时往右走。但是要比较首先需要找到比较的开始，也就是给定树的根在已知树中的定位，找到后，同时递归比较即可。

代码：

	public boolean isChildTree(BST<T> tree){
        BSTNode<T> cur = this.root;
        // 在当前BST树上找值为tree.root.getData()的节点
        while(cur != null){
            if(cur.getData().compareTo(tree.root.getData()) > 0){
                cur = cur.getLeft();
            } else if(cur.getData().compareTo(tree.root.getData()) < 0){
                cur = cur.getRight();
            } else {
                break;
            }
        }
        if(cur == null){
            return false;
        }

        return isChildTree(cur, tree.root);
    }

    private boolean isChildTree(BSTNode<T> f, BSTNode<T> c) {
        if(f == null && c == null){
            return true;
        }

        if(f == null){
            return false;
        }

        if(c == null){
            return true;
        }

        if(f.getData().compareTo(c.getData()) != 0){
            return false;
        }

        return isChildTree(f.getLeft(), c.getLeft())
                && isChildTree(f.getRight(), c.getRight());
    }