C++笔记：函数递归调用与汉诺塔问题

内容取自明日科技一书《C++从入门到精通》

递归函数定义

一种计算过程，如果其中每一步都要用到前一步或前几步的结果，称为递归的。用递归过程定义的函数，称为递归函数，例如连加、连乘及阶乘等。凡是递归的函数，都是可计算的，即能行的。

古典递归函数，是一种定义在自然数集合上的函数，它的未知值往往要通过有限次运算回归到已知值来求出，故称为“递归”。它是古典递归函数论的研究对象。

递归函数返回问题

代码片段出自C Primer Plus一书中对递归函数调用情况以及返回情况那一章节

/*理解C语言递归函数*/
#include<stdio.h>
#include<windows.h>
void up_and_down(int);
int  main(void)
{
 up_and_down(1);
 return 0;
}
void up_and_down(int n)
{
 SetConsoleOutputCP(65001);
 printf("调用层次 %d: 形参变量n的地址为 %p\n", n, &n);
 if (n < 4)
 {
  up_and_down(n + 1);//递归函数逐级返回，从此处开始，前面的语句不再执行
 }
 printf("调用层次 %d: 形参变量n的地址为 %p\n", n, &n);
}

输出：

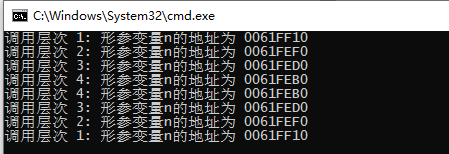
每一层递归函数执行完后，程序不能直接返回到main()中的初始调用部分，而是通过递归的每一级逐步返回。

汉诺塔问题

问题描述：
有3个立柱垂直立在地面，给这3个立柱分别命名为A,B,C。开始时立柱上有64个圆盘，这64个圆盘大小不一，并且按从小到大的顺序依次摆在立柱A上，现在要求：

• 将立柱A上的64个圆盘移动到立柱C上，每次只能移动一个圆盘
• 在移动过程中始终保持大盘在下，小盘在上

问题简化：
假设移动4个圆盘…

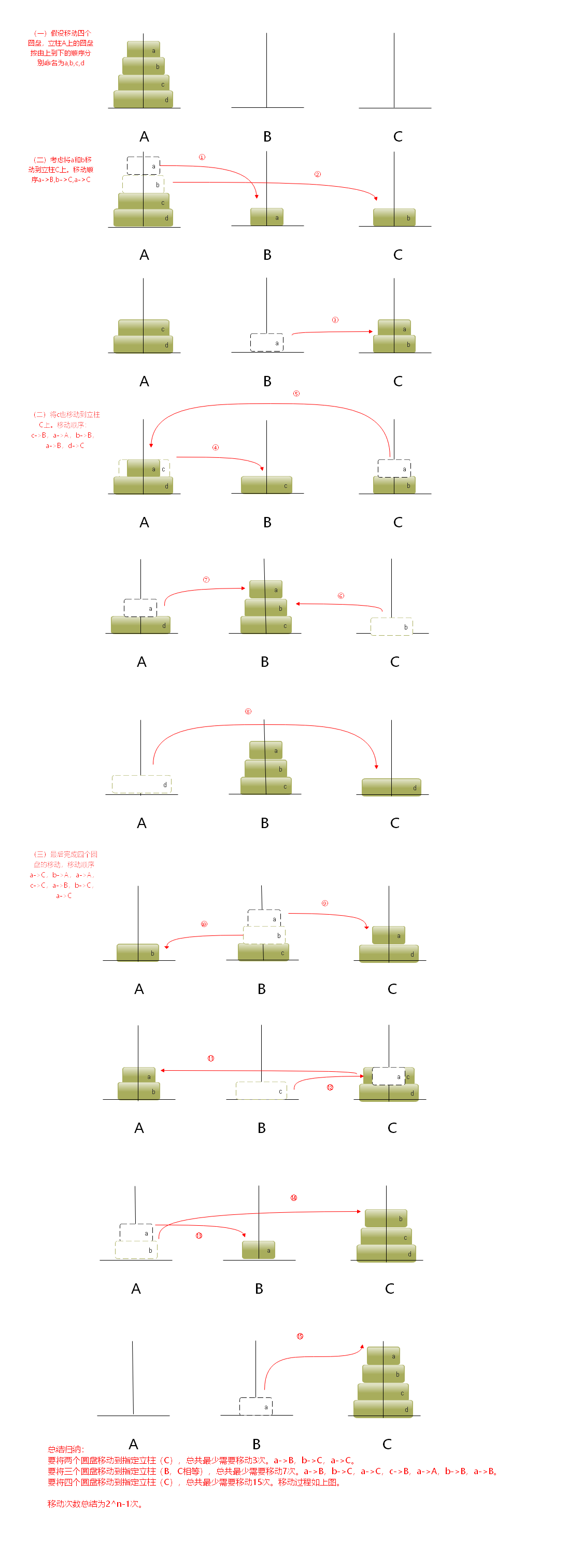
代码：

/*
将圆盘按照汉诺塔规则从A立柱全部移动到C立柱
*/
#include<iostream>
#include<windows.h>
using namespace std;
long count;//长整型
void move(int n,char A,char B,char C){//将n个圆盘从A立柱借助B立柱移动到C立柱上
 if(n==1){//当只有一个圆盘时
  printf("移动第%d次：%c->%c\n",++count,A,C);
 }else{
  move(n-1,A,C,B);//注意立柱顺序变为A、C、B
  printf("移动第%d次：%c->%c\n",++count,A,C);
  move(n-1,B,A,C);
 }
}
int main(){
 //SetConsoleOutputCP(65001); 
 count=0;//在主函数中将全局变量count初始化
 int n;//圆盘总数
 printf("请输入需要移动的总圆盘数：\n");
 cin>>n;
 move(n,'A','B','C');
 return 0;
}

输出：

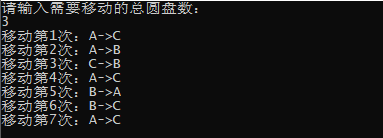
解释：
A->C指的是圆盘a从A柱移动到C柱
A->B指的是圆盘b从A柱移动到B柱
……

• 第23行第一次调用move时（主函数调用，进入层次一）：实参->‘A’，‘B’，‘C’，局部变量值->n=3，A=‘A’，B=‘B’，C=‘C’
• 第12行第一次递归调用move函数时（进入层次二）：实参->‘A’，‘C’，‘B’，局部变量值->n=2，A=‘A’，B=‘C’，C=‘B’
• 第12行第二次递归调用move函数时（进入层次三）：实参->‘A’，‘B’，‘C’，局部变量值->n=1，A=‘A’，B=‘B’，C=‘C’，符合if条件（n==1）打印"A->C"，然后返回层次二（此时层次二的局部环境变量为n=2，A=‘A’，B=‘C’，C=‘B’，第三次递归调用基于此环境），打印"A->B"
• 第14行第三次递归调用move函数时（进入层次三）：实参->‘C’，‘A’，‘B’，局部变量值->n=1,A=‘C’，B=‘A’，C=‘B‘