文章目录
GitHub: https://github.com/RealEmperor/Python-for-Data-Analysis
numpy
import numpy as np
from numpy.random import randn
#通用函数
arr = np.arange(10)
np.sqrt(arr)
array([ 0. , 1. , 1.41421356, 1.73205081, 2. ,
2.23606798, 2.44948974, 2.64575131, 2.82842712, 3. ])
np.exp(arr)
array([ 1.00000000e+00, 2.71828183e+00, 7.38905610e+00,
2.00855369e+01, 5.45981500e+01, 1.48413159e+02,
4.03428793e+02, 1.09663316e+03, 2.98095799e+03,
8.10308393e+03])
np.maximum 元素级最大值
x = randn(8)
y = randn(8)
print(x)
print(y)
# 元素级最大值
np.maximum(x, y)
[-1.03760196 -1.0035245 -0.19109603 2.27398057 -0.51605815 -1.25481649
-1.95118717 -0.09423245]
[-1.26195712 -0.70857631 -0.18729477 2.58847014 2.46277713 -1.04523397
1.13501218 1.3499591 ]
array([-1.03760196, -0.70857631, -0.18729477, 2.58847014, 2.46277713,
-1.04523397, 1.13501218, 1.3499591 ])
np.modf 按元素返回数组的小数部分和整数部分
arr = randn(7) * 5
print(arr)
# 按元素返回数组的小数部分和整数部分
np.modf(arr)
[ 8.01175821 3.46248512 -4.11785287 1.34226648 0.40194097 5.81213218
-0.40446832]
(array([ 0.01175821, 0.46248512, -0.11785287, 0.34226648, 0.40194097,
0.81213218, -0.40446832]), array([ 8., 3., -4., 1., 0., 5., -0.]))
np.meshgrid 从坐标向量返回坐标矩阵
###利用数组进行数据处理
# 向量化
points = np.arange(-5, 5, 0.01) # 1000 equally spaced points
# 从坐标向量返回坐标矩阵
xs, ys = np.meshgrid(points, points)
print(ys)
[[-5. -5. -5. ..., -5. -5. -5. ]
[-4.99 -4.99 -4.99 ..., -4.99 -4.99 -4.99]
[-4.98 -4.98 -4.98 ..., -4.98 -4.98 -4.98]
...,
[ 4.97 4.97 4.97 ..., 4.97 4.97 4.97]
[ 4.98 4.98 4.98 ..., 4.98 4.98 4.98]
[ 4.99 4.99 4.99 ..., 4.99 4.99 4.99]]
import matplotlib.pyplot as plt
z = np.sqrt(xs ** 2 + ys ** 2)
print(z)
plt.imshow(z, cmap=plt.cm.gray)
plt.colorbar()
plt.title("Image plot of $\sqrt{x^2 + y^2}$ for a grid of values")
plt.draw()
[[ 7.07106781 7.06400028 7.05693985 ..., 7.04988652 7.05693985
7.06400028]
[ 7.06400028 7.05692568 7.04985815 ..., 7.04279774 7.04985815
7.05692568]
[ 7.05693985 7.04985815 7.04278354 ..., 7.03571603 7.04278354
7.04985815]
...,
[ 7.04988652 7.04279774 7.03571603 ..., 7.0286414 7.03571603
7.04279774]
[ 7.05693985 7.04985815 7.04278354 ..., 7.03571603 7.04278354
7.04985815]
[ 7.06400028 7.05692568 7.04985815 ..., 7.04279774 7.04985815
7.05692568]]
np.where
# 将条件逻辑表达为数组运算
xarr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])
yarr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])
cond = np.array([True, False, True, True, False])
result = [(x if c else y)
for x, y, c in zip(xarr, yarr, cond)]
print(result)
[1.1000000000000001, 2.2000000000000002, 1.3, 1.3999999999999999, 2.5]
result = np.where(cond, xarr, yarr)
print(result)
[ 1.1 2.2 1.3 1.4 2.5]
arr = randn(4, 4)
print(arr)
print(np.where(arr > 0, 2, -2))
print(np.where(arr > 0, 2, arr)) # set only positive values to 2
[[-0.09677059 -0.78473401 -0.00841639 1.39892368]
[-1.14999224 0.33586593 -0.1844864 0.47664971]
[-0.67508722 0.56130304 -0.8018509 0.07338623]
[ 0.10375292 1.44174994 0.42788598 -0.66850794]]
[[-2 -2 -2 2]
[-2 2 -2 2]
[-2 2 -2 2]
[ 2 2 2 -2]]
[[-0.09677059 -0.78473401 -0.00841639 2. ]
[-1.14999224 2. -0.1844864 2. ]
[-0.67508722 2. -0.8018509 2. ]
[ 2. 2. 2. -0.66850794]]
"""
# 多条件一般表示方法
# Not to be executed
result = []
for i in range(n):
if cond1[i] and cond2[i]:
result.append(0)
elif cond1[i]:
result.append(1)
elif cond2[i]:
result.append(2)
else:
result.append(3)
# 多条件where表示方法
# Not to be executed
np.where(cond1 & cond2, 0,
np.where(cond1, 1,
np.where(cond2, 2, 3)))
# Not to be executed
result = 1 * cond1 + 2 * cond2 + 3 * -(cond1 | cond2)
"""
'\n# 多条件一般表示方法\n# Not to be executed\nresult = []\nfor i in range(n):\n if cond1[i] and cond2[i]:\n result.append(0)\n elif cond1[i]:\n result.append(1)\n elif cond2[i]:\n result.append(2)\n else:\n result.append(3)\n\n# 多条件where表示方法\n# Not to be executed\nnp.where(cond1 & cond2, 0,\n np.where(cond1, 1,\n np.where(cond2, 2, 3)))\n\n# Not to be executed\nresult = 1 * cond1 + 2 * cond2 + 3 * -(cond1 | cond2)\n'
数学与统计方法
randn 标准正态分布数据
# 数学与统计方法
arr = np.random.randn(5, 4) # 标准正态分布数据
print(arr.mean())
print(np.mean(arr))
print(arr.sum())
print(arr.mean(axis=1))
print(arr.sum(0))
arr = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
print(arr.cumsum(0))
print(arr.cumprod(1))
0.299738473867
0.299738473867
5.99476947734
[ 0.33172725 -0.49981575 0.35973217 0.39621625 0.91083245]
[ 4.58629248 2.22968175 -1.88744743 1.06624268]
[[ 0 1 2]
[ 3 5 7]
[ 9 12 15]]
[[ 0 0 0]
[ 3 12 60]
[ 6 42 336]]
用于布尔型数组的方法
# 用于布尔型数组的方法
arr = randn(100)
(arr > 0).sum() # 正值的数量
bools = np.array([False, False, True, False])
print(bools.any())
print(bools.all())
True
False
排序
# 排序
arr = randn(8)
print(arr)
arr.sort()
print(arr)
arr = randn(5, 3)
print(arr)
arr.sort(1)
print(arr)
[-0.17018254 1.29292169 1.87999871 -0.25529225 1.1058983 -0.27456269
-1.17911236 0.30155365]
[-1.17911236 -0.27456269 -0.25529225 -0.17018254 0.30155365 1.1058983
1.29292169 1.87999871]
[[-0.31552106 0.95227657 0.08006334]
[ 0.86493167 0.66028869 0.56929258]
[-1.30046025 -1.03020373 -0.80371581]
[-0.74412785 0.2413104 -0.81418268]
[-1.16001837 -0.70517682 -0.5816708 ]]
[[-0.31552106 0.08006334 0.95227657]
[ 0.56929258 0.66028869 0.86493167]
[-1.30046025 -1.03020373 -0.80371581]
[-0.81418268 -0.74412785 0.2413104 ]
[-1.16001837 -0.70517682 -0.5816708 ]]
5%分位数
large_arr = randn(1000)
large_arr.sort()
large_arr[int(0.05 * len(large_arr))] # 5%分位数
-1.7061490455426676
np.unique 唯一化 以及其他的集合逻辑
# 唯一化以及其他的集合逻辑
names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
np.unique(names)
array(['Bob', 'Joe', 'Will'],
dtype='<U4')
ints = np.array([3, 3, 3, 2, 2, 1, 1, 4, 4])
np.unique(ints)
array([1, 2, 3, 4])
sorted(set(names))
['Bob', 'Joe', 'Will']
values = np.array([6, 0, 0, 3, 2, 5, 6])
np.in1d(values, [2, 3, 6])
array([ True, False, False, True, True, False, True], dtype=bool)
线性代数
#线性代数
x = np.array([[1., 2., 3.], [4., 5., 6.]])
y = np.array([[6., 23.], [-1, 7], [8, 9]])
print(x)
print(y)
print(x.dot(y)) # 等价于np.dot(x, y)
print(np.dot(x, np.ones(3)))
np.random.seed(12345)
from numpy.linalg import inv, qr
X = randn(5, 5)
mat = X.T.dot(X)
# 计算矩阵的逆矩阵
inv(mat)
mat.dot(inv(mat))
# 计算矩阵的QR因子分解
q, r = qr(mat)
print(r)
[[ 1. 2. 3.]
[ 4. 5. 6.]]
[[ 6. 23.]
[ -1. 7.]
[ 8. 9.]]
[[ 28. 64.]
[ 67. 181.]]
[ 6. 15.]
[[ -6.92714002 7.38899524 6.12272905 -7.11625341 -4.92150833]
[ 0. -3.97347612 -0.86707993 2.97472904 -5.74024113]
[ 0. 0. -10.26810228 1.89090298 1.60790112]
[ 0. 0. 0. -1.29964934 3.35772244]
[ 0. 0. 0. 0. 0.55705805]]
随机数生成
#随机数生成
samples = np.random.normal(size=(4, 4))
print(samples)
[[ 1.24121276e-01 3.02613562e-01 5.23772068e-01 9.40277775e-04]
[ 1.34380979e+00 -7.13543985e-01 -8.31153539e-01 -2.37023165e+00]
[ -1.86076079e+00 -8.60757398e-01 5.60145293e-01 -1.26593449e+00]
[ 1.19827125e-01 -1.06351245e+00 3.32882716e-01 -2.35941881e+00]]
范例:随机漫步
# 范例:随机漫步
import random
position = 0
walk = [position]
steps = 1000
for i in range(steps):
step = 1 if random.randint(0, 1) else -1
position += step
walk.append(position)
print(walk)
[0, 1, 0, -1, 0, -1, 0, -1, -2, -1, 0, -1, 0, 1, 2, 1, 0, -1, -2, -1, -2, -3, -4, -5, -4, -3, -2, -3, -4, -5, -6, -5, -4, -3, -4, -3, -4, -5, -4, -5, -6, -7, -6, -5, -4, -5, -6, -7, -6, -7, -6, -7, -6, -5, -4, -3, -4, -3, -4, -3, -2, -3, -4, -3, -2, -3, -4, -5, -6, -7, -8, -9, -8, -9, -8, -9, -8, -7, -6, -5, -6, -5, -6, -7, -8, -9, -8, -7, -8, -9, -10, -11, -12, -13, -12, -11, -12, -11, -12, -11, -12, -11, -12, -11, -10, -11, -12, -11, -12, -13, -12, -11, -12, -11, -10, -11, -12, -13, -12, -11, -10, -9, -10, -9, -10, -11, -10, -11, -10, -9, -8, -9, -10, -11, -12, -13, -12, -13, -14, -15, -14, -13, -12, -13, -12, -11, -10, -9, -8, -9, -8, -9, -8, -9, -8, -9, -8, -9, -10, -9, -8, -7, -8, -9, -10, -11, -12, -11, -12, -11, -12, -13, -12, -13, -12, -11, -12, -11, -10, -9, -8, -7, -6, -7, -6, -7, -6, -5, -6, -5, -4, -5, -6, -7, -8, -7, -8, -7, -6, -7, -6, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 1, 0, 1, 0, 1, 2, 1, 2, 1, 0, -1, 0, 1, 0, 1, 0, 1, 2, 1, 0, -1, -2, -3, -2, -3, -2, -3, -4, -3, -2, -1, -2, -3, -4, -3, -2, -3, -4, -3, -4, -5, -6, -7, -8, -9, -10, -9, -8, -7, -8, -7, -8, -7, -6, -7, -6, -7, -6, -7, -6, -5, -6, -5, -6, -5, -4, -5, -6, -5, -6, -7, -6, -7, -8, -7, -6, -7, -6, -5, -4, -3, -4, -5, -4, -5, -6, -5, -6, -5, -4, -3, -4, -3, -4, -5, -6, -5, -6, -5, -6, -5, -4, -3, -2, -1, -2, -1, -2, -1, -2, -3, -4, -3, -4, -3, -4, -3, -2, -1, -2, -1, 0, 1, 2, 1, 0, 1, 2, 1, 2, 1, 2, 3, 2, 3, 2, 3, 2, 1, 0, -1, 0, -1, 0, -1, 0, -1, 0, -1, -2, -1, 0, 1, 2, 3, 4, 5, 4, 5, 4, 3, 2, 3, 4, 5, 6, 5, 6, 7, 6, 5, 6, 5, 4, 5, 4, 5, 6, 7, 6, 5, 4, 5, 4, 3, 4, 5, 4, 5, 4, 3, 4, 5, 4, 5, 6, 7, 6, 7, 6, 7, 8, 9, 10, 9, 10, 9, 10, 9, 10, 9, 8, 9, 8, 7, 8, 9, 10, 11, 12, 13, 12, 11, 10, 11, 12, 13, 14, 15, 14, 15, 16, 15, 16, 15, 14, 13, 14, 13, 14, 13, 12, 11, 10, 9, 10, 11, 10, 11, 12, 11, 12, 11, 10, 9, 10, 9, 8, 9, 10, 9, 8, 7, 8, 7, 6, 5, 6, 7, 6, 7, 8, 9, 10, 11, 12, 13, 12, 13, 14, 13, 12, 13, 12, 13, 12, 11, 12, 11, 10, 11, 12, 13, 12, 11, 10, 9, 10, 11, 12, 13, 12, 13, 12, 13, 12, 13, 14, 15, 14, 13, 12, 13, 14, 15, 14, 15, 14, 15, 14, 15, 16, 17, 16, 17, 18, 17, 16, 17, 18, 19, 18, 19, 20, 21, 22, 21, 22, 21, 20, 19, 18, 17, 16, 15, 16, 15, 16, 17, 18, 19, 20, 19, 18, 19, 20, 19, 18, 19, 18, 19, 18, 17, 18, 19, 18, 17, 16, 15, 14, 13, 12, 13, 14, 15, 14, 13, 14, 13, 12, 13, 12, 13, 12, 11, 10, 11, 12, 13, 14, 15, 14, 13, 14, 13, 12, 13, 14, 15, 14, 13, 14, 15, 16, 17, 18, 19, 18, 19, 20, 19, 20, 19, 18, 19, 20, 21, 20, 21, 20, 19, 18, 19, 20, 19, 18, 17, 18, 19, 18, 17, 16, 15, 14, 15, 14, 13, 12, 11, 12, 11, 10, 11, 12, 11, 10, 9, 8, 9, 10, 9, 10, 9, 10, 11, 10, 11, 12, 13, 12, 13, 12, 13, 12, 13, 14, 13, 12, 13, 12, 13, 14, 13, 12, 13, 12, 13, 12, 13, 12, 13, 12, 11, 10, 11, 10, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 3, 4, 3, 4, 5, 4, 5, 4, 5, 4, 5, 6, 7, 6, 7, 6, 5, 6, 7, 8, 9, 8, 9, 10, 9, 8, 9, 10, 11, 10, 11, 12, 13, 12, 11, 12, 13, 14, 15, 14, 15, 16, 17, 16, 15, 14, 15, 16, 15, 14, 13, 14, 15, 16, 15, 16, 17, 18, 17, 16, 15, 16, 17, 18, 17, 18, 19, 20, 19, 20, 19, 20, 19, 18, 19, 18, 17, 16, 15, 14, 13, 14, 15, 16, 15, 16, 17, 18, 19, 20, 21, 20, 19, 18, 17, 16, 15, 16, 17, 16, 15, 16, 15, 14, 13, 12, 11, 10, 11, 12, 11, 12, 11, 12, 11, 10, 9, 10, 9, 8, 7, 8, 7, 8, 7, 8, 7, 6, 7, 6, 5, 6, 5, 4, 3, 2, 1, 2, 1, 0, 1, 0, 1, 0, 1, 2, 3, 4, 3, 4, 5, 6, 5, 4, 5, 4, 3, 4, 3, 2, 3, 2, 3, 4, 3, 2, 3, 2, 3, 4, 3, 2, 1, 2, 1, 0, 1, 2, 3, 2, 3, 2, 1, 2, 3, 4, 3, 4, 3, 2, 3, 2, 3, 4, 5, 4, 3, 4, 3, 4, 5, 4, 5, 6, 5, 4, 5, 6, 7, 8, 9, 8, 9, 8, 7, 6, 7, 8, 7, 6, 7, 8, 9, 10, 9, 10, 11, 12, 13, 14, 13, 12, 11, 12, 11, 12, 13, 12, 11, 10, 11, 12, 11, 10, 11, 10, 9, 8, 7, 6, 5, 6, 5, 6, 7, 6, 5, 6, 5, 4, 3, 2, 1, 0, 1, 2, 3, 2, 1, 0, 1, 0, -1, 0, 1, 2, 1, 0, -1, -2, -3, -4, -5, -4, -3, -4, -3, -4, -3, -4, -5, -4, -5, -4]
np.random.seed(12345)
nsteps = 1000
draws = np.random.randint(0, 2, size=nsteps)
steps = np.where(draws > 0, 1, -1)
walk = steps.cumsum()
print(walk)
print(walk.min())
print(walk.max())
print((np.abs(walk) >= 10).argmax())
[-1 0 1 2 1 2 1 0 1 0 1 2 1 2 3 2 3 4 5 4 3 2 3 4 5
4 5 4 3 4 5 6 7 8 7 8 9 10 11 12 13 12 11 12 13 12 11 12 13 14
15 14 15 16 17 18 17 18 19 18 19 18 17 18 19 20 19 18 19 18 19 18 17 16 17
18 17 16 15 14 13 12 13 12 11 10 11 10 9 10 11 12 13 14 15 14 13 12 13 12
11 12 11 12 11 12 11 10 9 10 11 10 9 10 9 10 9 8 9 10 9 10 11 10 9
10 9 8 9 10 11 12 11 10 9 10 9 10 9 8 9 10 9 10 9 10 9 10 11 12
11 12 11 10 9 10 11 10 9 8 7 6 5 6 7 8 7 6 7 6 7 6 7 6 5
6 7 6 7 8 7 8 9 8 7 8 7 6 7 8 9 10 9 10 11 10 11 12 13 12
11 10 9 8 9 10 11 10 9 10 9 10 9 10 9 8 7 6 7 6 5 6 7 8 7
6 5 6 7 6 7 8 7 8 7 6 5 4 3 4 3 2 3 4 5 6 7 6 5 4
5 4 3 2 3 4 5 6 5 6 5 6 7 6 7 8 7 6 7 6 7 8 9 8 9
8 9 8 7 6 5 4 3 2 1 0 1 0 -1 -2 -1 -2 -3 -2 -1 0 1 2 3 4
5 6 7 6 5 6 5 4 3 2 1 2 3 4 3 4 5 4 5 4 5 4 3 2 1
2 3 4 5 6 5 4 5 6 5 6 7 6 5 6 5 4 5 4 3 4 5 6 5 4
5 6 7 6 7 8 7 6 5 4 5 6 7 6 5 6 7 6 7 8 9 10 11 10 11
10 11 10 9 10 11 12 11 10 11 10 11 10 11 12 13 14 13 12 11 12 11 10 9 8
9 8 7 8 7 6 7 8 9 8 9 8 9 10 11 12 13 14 15 14 13 12 13 14 15
14 15 16 17 16 15 16 15 16 17 18 19 18 19 18 17 16 15 14 13 12 13 12 13 14
13 14 13 14 15 14 13 12 11 10 11 10 11 12 11 12 11 10 11 12 11 12 13 12 13
14 13 14 13 14 15 14 15 14 13 12 11 10 9 8 7 8 7 6 5 4 5 4 3 4
3 2 3 4 5 6 5 4 3 2 1 2 1 2 3 4 3 4 3 4 5 4 3 4 3
4 5 4 5 4 3 2 3 2 1 2 3 2 1 2 1 2 1 0 1 2 1 2 1 2
3 2 1 2 3 4 5 4 3 2 3 2 1 2 1 2 3 2 1 2 3 4 3 2 3
4 5 6 7 6 5 4 3 2 1 2 3 2 1 2 3 4 5 6 7 6 7 8 7 8
7 8 9 8 9 8 7 6 5 6 5 4 3 4 3 4 5 6 5 6 7 8 9 8 9
8 9 10 9 10 11 12 13 14 13 12 11 12 11 12 13 12 13 14 13 14 13 12 13 12
13 14 15 14 13 12 11 10 9 10 9 8 7 6 7 8 7 8 9 8 9 10 9 10 11
10 11 10 11 10 11 10 9 10 11 12 13 12 13 12 13 14 15 14 13 12 13 12 11 10
11 10 9 8 7 6 7 6 5 4 5 4 5 6 5 4 5 4 5 4 3 4 3 4 3
4 5 6 7 8 9 8 7 8 9 10 11 10 9 8 7 6 7 8 7 8 7 8 7 6
5 6 5 6 7 8 7 8 9 10 9 8 9 8 9 10 9 10 9 8 9 8 7 8 9
8 9 8 9 8 9 8 9 10 11 10 11 12 11 12 13 14 15 14 13 14 15 16 15 14
15 16 17 16 15 14 13 14 13 14 13 14 13 14 13 14 15 16 17 16 17 18 17 16 17
18 17 18 17 18 19 20 19 18 19 20 19 18 17 18 17 18 19 20 19 18 17 16 15 16
17 18 19 20 21 22 21 20 21 22 21 22 21 22 21 20 21 22 23 22 23 22 23 22 21
22 23 24 23 24 23 24 25 24 25 26 27 28 29 28 29 28 27 26 25 26 27 26 27 28
27 26 27 26 27 28 27 28 29 30 31 30 31 30 29 30 29 28 29 28 29 30 29 28 27
26 25 24 23 22 23 22 23 22 21 20 19 18 17 18 17 18 19 18 19 18 17 16 17 16
17 18 17 18 17 16 15 14 13 14 15 16 17 16 17 18 17 16 15 14 13 14 13 14 13
14 15 14 13 14 13 14 15 16 15 16 15 16 15 14 15 14 13 14 13 12 13 12 13 14]
-3
31
37
# 一次模拟多个随机漫步
nwalks = 5000
nsteps = 1000
draws = np.random.randint(0, 2, size=(nwalks, nsteps)) # 0 or 1
steps = np.where(draws > 0, 1, -1)
walks = steps.cumsum(1)
print(walks)
print(walks.max())
print(walks.min())
hits30 = (np.abs(walks) >= 30).any(1)
print(hits30)
print(hits30.sum()) # 到达30或-30的数量
crossing_times = (np.abs(walks[hits30]) >= 30).argmax(1)
print(crossing_times.mean())
[[ 1 0 1 ..., 8 7 8]
[ 1 0 -1 ..., 34 33 32]
[ 1 0 -1 ..., 4 5 4]
...,
[ 1 2 1 ..., 24 25 26]
[ 1 2 3 ..., 14 13 14]
[ -1 -2 -3 ..., -24 -23 -22]]
138
-133
[False True False ..., False True False]
3410
498.88973607
steps = np.random.normal(loc=0, scale=0.25, size=(nwalks, nsteps))
print(steps)
[[-0.02565707 0.36310961 0.41720151 ..., 0.15726638 -0.16256773
0.05423703]
[-0.10456259 0.07877516 0.19110411 ..., 0.07678875 -0.18545695
0.0333151 ]
[-0.16728617 0.12034941 -0.30427248 ..., -0.30982359 -0.17291787
0.02772071]
...,
[ 0.27987403 0.05477886 -0.02167382 ..., 0.02795479 0.25268149
0.06510672]
[ 0.31853634 -0.15109745 -0.1121375 ..., 0.14705719 0.18206871
-0.02473096]
[-0.13101904 -0.24008233 -0.03925202 ..., -0.18320903 -0.20967376
0.20705573]]
利用NumPy进行历史股价分析
#利用NumPy进行历史股价分析
import sys
# 读入文件
fname = 'data\AAPL.csv'
# c:价格,v:成交量
c, v = np.loadtxt(fname, delimiter=',', usecols=(6, 7), unpack=True)
# 计算成交量加权平均价格
vwap = np.average(c, weights=v)
print("vwap =", vwap)
# 算术平均值函数
print("mean =", np.mean(c))
# 时间加权平均价格
t = np.arange(len(c))
print("twap =", np.average(c, weights=t))
# 寻找最大值和最小值
h, l = np.loadtxt(fname, delimiter=',', usecols=(4, 5), unpack=True)
print("highest =", np.max(h))
print("lowest =", np.min(l))
print((np.max(h) + np.min(l)) / 2)
print("Spread high price", np.ptp(h))
print("Spread low price", np.ptp(l))
VWAP = 350.589549353
mean = 351.037666667
twap = 352.428321839
highest = 364.9
lowest = 333.53
349.215
Spread high price 24.86
Spread low price 26.97
统计分析
# 统计分析
c = np.loadtxt(fname, delimiter=',', usecols=(6,), unpack=True)
print("median =", np.median(c))
msorted = np.msort(c)
print("sorted =", msorted)
N = len(c)
print("middle =", msorted[int((N - 1) / 2)])
print("average middle =", (msorted[int(N / 2)] + msorted[int((N - 1) / 2)]) / 2)
print("variance =", np.var(c))
print("variance from definition =", np.mean((c - c.mean()) ** 2))
median = 352.055
sorted = [ 336.1 338.61 339.32 342.62 342.88 343.44 344.32 345.03 346.5
346.67 348.16 349.31 350.56 351.88 351.99 352.12 352.47 353.21
354.54 355.2 355.36 355.76 356.85 358.16 358.3 359.18 359.56
359.9 360. 363.13]
middle = 351.99
average middle = 352.055
variance = 50.1265178889
variance from definition = 50.1265178889
股票收益率
# 股票收益率
c = np.loadtxt(fname, delimiter=',', usecols=(6,), unpack=True)
returns = np.diff(c) / c[: -1]
print("Standard deviation =", np.std(returns))
logreturns = np.diff(np.log(c))
posretindices = np.where(returns > 0)
print("Indices with positive returns", posretindices)
daily_volatility = np.std(logreturns) / np.mean(logreturns)
annual_volatility = daily_volatility * np.sqrt(252.)
print('Annual volatility', annual_volatility)
print('Monthly volatility', annual_volatility / np.sqrt(12))
Standard deviation = 0.0129221344368
Indices with positive returns (array([ 0, 1, 4, 5, 6, 7, 9, 10, 11, 12, 16, 17, 18, 19, 21, 22, 23,
25, 28], dtype=int64),)
Annual volatility 129.274789911
Monthly volatility 37.3184173773
日期分析
# 日期分析
from datetime import datetime
# Monday 0
# Tuesday 1
# Wednesday 2
# Thursday 3
# Friday 4
# Saturday 5
# Sunday 6
def datestr2num(s):
s = str(s, 'utf-8')
return datetime.strptime(s, "%d-%m-%Y").date().weekday()
dates, close = np.loadtxt(fname, delimiter=',', usecols=(1, 6),
converters={1: datestr2num},
unpack=True)
print("Dates =", dates)
averages = np.zeros(5)
for i in range(5):
indices = np.where(dates == i)
prices = np.take(close, indices)
avg = np.mean(prices)
print("Day", i, "prices", prices, "Average", avg)
averages[i] = avg
top = np.max(averages)
print("Highest average", top)
print("Top day of the week", np.argmax(averages))
bottom = np.min(averages)
print("Lowest average", bottom)
print("Bottom day of the week", np.argmin(averages))
Dates = [ 4. 0. 1. 2. 3. 4. 0. 1. 2. 3. 4. 0. 1. 2. 3. 4. 1. 2.
3. 4. 0. 1. 2. 3. 4. 0. 1. 2. 3. 4.]
Day 0 prices [[ 339.32 351.88 359.18 353.21 355.36]] Average 351.79
Day 1 prices [[ 345.03 355.2 359.9 338.61 349.31 355.76]] Average 350.635
Day 2 prices [[ 344.32 358.16 363.13 342.62 352.12 352.47]] Average 352.136666667
Day 3 prices [[ 343.44 354.54 358.3 342.88 359.56 346.67]] Average 350.898333333
Day 4 prices [[ 336.1 346.5 356.85 350.56 348.16 360. 351.99]] Average 350.022857143
Highest average 352.136666667
Top day of the week 2
Lowest average 350.022857143
Bottom day of the week 4
周汇总
# 周汇总
def datestr2num(s):
s = str(s, 'utf-8')
return datetime.strptime(s, "%d-%m-%Y").date().weekday()
dates, open, high, low, close = np.loadtxt(fname, delimiter=',',
usecols=(1, 3, 4, 5, 6), converters={1: datestr2num}, unpack=True)
close = close[:16]
dates = dates[:16]
# get first Monday
first_monday = np.ravel(np.where(dates == 0))[0]
print("The first Monday index is", first_monday)
# get last Friday
last_friday = np.ravel(np.where(dates == 4))[-1]
print("The last Friday index is", last_friday)
weeks_indices = np.arange(first_monday, last_friday + 1)
print("Weeks indices initial", weeks_indices)
weeks_indices = np.split(weeks_indices, 3)
print("Weeks indices after split", weeks_indices)
def summarize(a, o, h, l, c):
monday_open = o[a[0]]
week_high = np.max(np.take(h, a))
week_low = np.min(np.take(l, a))
friday_close = c[a[-1]]
return ("APPL", monday_open, week_high, week_low, friday_close)
weeksummary = np.apply_along_axis(summarize, 1, weeks_indices, open, high, low, close)
print("Week summary", weeksummary)
np.savetxt("data/weeksummary.csv", weeksummary, delimiter=",", fmt="%s")
The first Monday index is 1
The last Friday index is 15
Weeks indices initial [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15]
Weeks indices after split [array([1, 2, 3, 4, 5], dtype=int64), array([ 6, 7, 8, 9, 10], dtype=int64), array([11, 12, 13, 14, 15], dtype=int64)]
Week summary [['APPL' '335.8' '346.7' '334.3' '346.5']
['APPL' '347.8' '360.0' '347.6' '356.8']
['APPL' '356.7' '364.9' '349.5' '350.5']]
真实波动幅度均值
# 真实波动幅度均值
h, l, c = np.loadtxt(fname, delimiter=',', usecols=(4, 5, 6), unpack=True)
N = 20
h = h[-N:]
l = l[-N:]
print("len(h)", len(h), "len(l)", len(l))
print("Close", c)
previousclose = c[-N - 1: -1]
print("len(previousclose)", len(previousclose))
print("Previous close", previousclose)
truerange = np.maximum(h - l, h - previousclose, previousclose - l)
print("True range", truerange)
atr = np.zeros(N)
atr[0] = np.mean(truerange)
for i in range(1, N):
atr[i] = (N - 1) * atr[i - 1] + truerange[i]
atr[i] /= N
print("ATR", atr)
len(h) 20 len(l) 20
Close [ 336.1 339.32 345.03 344.32 343.44 346.5 351.88 355.2 358.16
354.54 356.85 359.18 359.9 363.13 358.3 350.56 338.61 342.62
342.88 348.16 353.21 349.31 352.12 359.56 360. 355.36 355.76
352.47 346.67 351.99]
len(previousclose) 20
Previous close [ 354.54 356.85 359.18 359.9 363.13 358.3 350.56 338.61 342.62
342.88 348.16 353.21 349.31 352.12 359.56 360. 355.36 355.76
352.47 346.67]
True range [ 4.26 2.77 2.42 5. 3.75 9.98 7.68 6.03 6.78 5.55
6.89 8.04 5.95 7.67 2.54 10.36 5.15 4.16 4.87 7.32]
ATR [ 5.8585 5.704075 5.53987125 5.51287769 5.4247338 5.65249711
5.75387226 5.76767864 5.81829471 5.80487998 5.85913598 5.96817918
5.96727022 6.05240671 5.87678637 6.10094705 6.0533997 5.95872972
5.90429323 5.97507857]
简单移动平均线
# 简单移动平均线
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
N = 5
weights = np.ones(N) / N
print("Weights", weights)
c = np.loadtxt(fname, delimiter=',', usecols=(6,), unpack=True)
sma = np.convolve(weights, c)[N - 1:-N + 1]
t = np.arange(N - 1, len(c))
plot(t, c[N - 1:], lw=1.0)
plot(t, sma, lw=2.0)
show()
Weights [ 0.2 0.2 0.2 0.2 0.2]
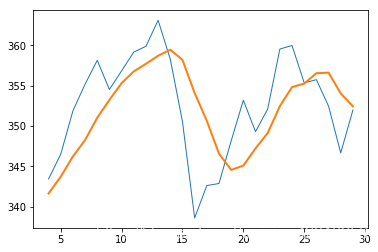
指数移动平均线
# 指数移动平均线
x = np.arange(5)
print("Exp", np.exp(x))
print("Linspace", np.linspace(-1, 0, 5))
N = 5
weights = np.exp(np.linspace(-1., 0., N))
weights /= weights.sum()
print("Weights", weights)
c = np.loadtxt(fname, delimiter=',', usecols=(6,), unpack=True)
ema = np.convolve(weights, c)[N - 1:-N + 1]
t = np.arange(N - 1, len(c))
plot(t, c[N - 1:], lw=1.0)
plot(t, ema, lw=2.0)
show()
Exp [ 1. 2.71828183 7.3890561 20.08553692 54.59815003]
Linspace [-1. -0.75 -0.5 -0.25 0. ]
Weights [ 0.11405072 0.14644403 0.18803785 0.24144538 0.31002201]
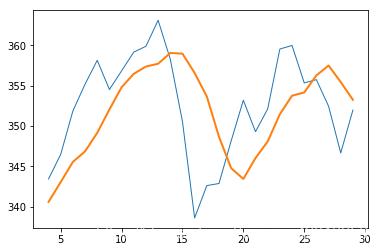
布林带
# 布林带
N = 5
weights = np.ones(N) / N
print("Weights", weights)
c = np.loadtxt(fname, delimiter=',', usecols=(6,), unpack=True)
sma = np.convolve(weights, c)[N - 1:-N + 1]
deviation = []
C = len(c)
for i in range(N - 1, C):
if i + N < C:
dev = c[i: i + N]
else:
dev = c[-N:]
averages = np.zeros(N)
averages.fill(sma[i - N - 1])
dev = dev - averages
dev = dev ** 2
dev = np.sqrt(np.mean(dev))
deviation.append(dev)
deviation = 2 * np.array(deviation)
print(len(deviation), len(sma))
upperBB = sma + deviation
lowerBB = sma - deviation
c_slice = c[N - 1:]
between_bands = np.where((c_slice < upperBB) & (c_slice > lowerBB))
print(lowerBB[between_bands])
print(c[between_bands])
print(upperBB[between_bands])
between_bands = len(np.ravel(between_bands))
print("Ratio between bands", float(between_bands) / len(c_slice))
t = np.arange(N - 1, C)
plot(t, c_slice, lw=1.0)
plot(t, sma, lw=2.0)
plot(t, upperBB, lw=3.0)
plot(t, lowerBB, lw=4.0)
show()
Weights [ 0.2 0.2 0.2 0.2 0.2]
26 26
[ 329.23044409 335.70890572 318.53386282 321.90858271 327.74175968
331.5628136 337.94259734 343.84172744 339.99900409 336.58687297
333.15550418 328.64879207 323.61483771 327.25667796 334.30323599
335.79295948 326.55905786 324.27329493 325.47601386 332.85867025
341.63882551 348.75558399 348.48014357 348.01342992 343.56371701
341.85163786]
[ 336.1 339.32 345.03 344.32 343.44 346.5 351.88 355.2 358.16
354.54 356.85 359.18 359.9 363.13 358.3 350.56 338.61 342.62
342.88 348.16 353.21 349.31 352.12 359.56 360. 355.36]
[ 354.05355591 351.73509428 373.93413718 374.62741729 374.33024032
374.9491864 372.70940266 369.73027256 375.45299591 380.85312703
385.78849582 387.77920793 384.58516229 374.03132204 358.88476401
353.33904052 363.63294214 370.19870507 372.79598614 372.08532975
368.04117449 361.78441601 364.63985643 365.24657008 364.54028299
363.04836214]
Ratio between bands 1.0
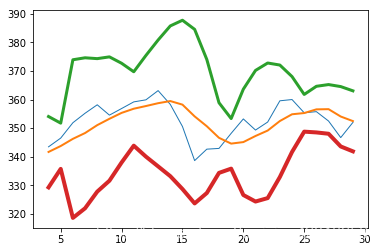
线性模型
# 线性模型
# N = int(sys.argv[1])
N = 5
c = np.loadtxt(fname, delimiter=',', usecols=(6,), unpack=True)
b = c[-N:]
b = b[::-1]
print("b", b)
A = np.zeros((N, N), float)
print("Zeros N by N", A)
for i in range(N):
A[i,] = c[-N - 1 - i: - 1 - i]
print("A", A)
(x, residuals, rank, s) = np.linalg.lstsq(A, b)
print(x, residuals, rank, s)
print(np.dot(b, x))
b [ 351.99 346.67 352.47 355.76 355.36]
Zeros N by N [[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
A [[ 360. 355.36 355.76 352.47 346.67]
[ 359.56 360. 355.36 355.76 352.47]
[ 352.12 359.56 360. 355.36 355.76]
[ 349.31 352.12 359.56 360. 355.36]
[ 353.21 349.31 352.12 359.56 360. ]]
[ 0.78111069 -1.44411737 1.63563225 -0.89905126 0.92009049] [] 5 [ 1.77736601e+03 1.49622969e+01 8.75528492e+00 5.15099261e+00
1.75199608e+00]
357.939161015
趋势线
# 趋势线
def fit_line(t, y):
A = np.vstack([t, np.ones_like(t)]).T
return np.linalg.lstsq(A, y)[0]
h, l, c = np.loadtxt(fname, delimiter=',', usecols=(4, 5, 6), unpack=True)
pivots = (h + l + c) / 3
print("Pivots", pivots)
t = np.arange(len(c))
sa, sb = fit_line(t, pivots - (h - l))
ra, rb = fit_line(t, pivots + (h - l))
support = sa * t + sb
resistance = ra * t + rb
condition = (c > support) & (c < resistance)
print("Condition", condition)
between_bands = np.where(condition)
print(support[between_bands])
print(c[between_bands])
print(resistance[between_bands])
between_bands = len(np.ravel(between_bands))
print("Number points between bands", between_bands)
print("Ratio between bands", float(between_bands) / len(c))
print("Tomorrows support", sa * (t[-1] + 1) + sb)
print("Tomorrows resistance", ra * (t[-1] + 1) + rb)
a1 = c[c > support]
a2 = c[c < resistance]
print("Number of points between bands 2nd approach", len(np.intersect1d(a1, a2)))
plot(t, c)
plot(t, support)
plot(t, resistance)
show()
Pivots [ 338.01 337.88666667 343.88666667 344.37333333 342.07666667
345.57 350.92333333 354.29 357.34333333 354.18
356.06333333 358.45666667 359.14 362.84333333 358.36333333
353.19333333 340.57666667 341.95666667 342.13333333 347.13
353.12666667 350.90333333 351.62333333 358.42333333 359.34666667
356.11333333 355.13666667 352.61 347.11333333 349.77 ]
Condition [False False True True True True True False False True False False
False False False True False False False True True True True False
False True True True False True]
[ 341.92421382 342.19081893 342.45742405 342.72402917 342.99063429
343.79044964 345.39008034 346.4565008 346.72310592 346.98971104
347.25631615 348.0561315 348.32273662 348.58934174 349.12255197]
[ 345.03 344.32 343.44 346.5 351.88 354.54 350.56 348.16 353.21
349.31 352.12 355.36 355.76 352.47 351.99]
[ 352.61688271 352.90732765 353.19777259 353.48821753 353.77866246
354.64999728 356.39266691 357.55444667 357.84489161 358.13533655
358.42578149 359.2971163 359.58756124 359.87800618 360.45889606]
Number points between bands 15
Ratio between bands 0.5
Tomorrows support 349.389157088
Tomorrows resistance 360.749340996
Number of points between bands 2nd approach 15
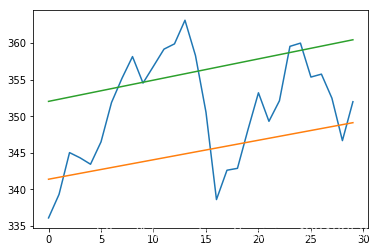
参考资料:炼数成金Python数据分析课程




 这篇博客介绍了Python数据分析中NumPy库的基础使用,包括元素级最大值、小数和整数部分分离、坐标矩阵生成、条件判断操作,以及数学统计方法如标准正态分布、排序、唯一化等。此外,还探讨了线性代数中的随机数生成,并通过实例展示了如何利用NumPy进行历史股价分析,涉及股票收益率、日期处理、波动幅度、移动平均线和趋势线的计算。
这篇博客介绍了Python数据分析中NumPy库的基础使用,包括元素级最大值、小数和整数部分分离、坐标矩阵生成、条件判断操作,以及数学统计方法如标准正态分布、排序、唯一化等。此外,还探讨了线性代数中的随机数生成,并通过实例展示了如何利用NumPy进行历史股价分析,涉及股票收益率、日期处理、波动幅度、移动平均线和趋势线的计算。
















 547
547

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








