2进制-16进制-补码

最新推荐文章于 2025-06-26 20:46:53 发布

原创最新推荐文章于 2025-06-26 20:46:53 发布 · 1.5w 阅读

13 ·

CC 4.0 BY-SA版权

文章标签：

#2进制 #16进制 #补码

JavaBasic 专栏收录该内容

9 篇文章

订阅专栏

进制的计算

10进制

规律: 逢10进1
数字: 0 1 2 3 4 5 6 7 8 9
权(weight): 万千百十个
基数(base): 10

2进制

规律: 逢2进1
数字: 1 2
权(weight): …32 16 8 4 2 1
基数(base): 2
计算机为啥使用2进制:

2进制其设备制造成本低!适合规模化生产



         * 00000000 00000000 00000000 00000000 ----> 0
         * 00000000 00000000 00000000 00000001 ----> 1
         * 00000000 00000000 00000000 00000010 ----> 2
         * 00000000 00000000 00000000 00000011 ----> 3
         * 00000000 00000000 00000000 00000100 ----> 4
         * 00000000 00000000 00000000 00000101 ----> 5
         * 00000000 00000000 00000000 00000110 ----> 6
         * 00000000 00000000 00000000 00000111 ----> 7
         * 00000000 00000000 00000000 00001000 ----> 8
	     * 111010 ---> 58
	     * 110110 ---> 54
	     * 101110 ---> 46
	     * 1101101 ---> 109
	     * 1101000 ---> 104
	     * 1111010 ---> 122
	     * 1110010 ---> 114
	     * 1100111 ---> 102
	     * 1010100 ---> 84
	     * 1000101 ---> 69
	     * 10001110 ---> 142
	     * 10010000 ---> 146
	     * 10000111 ---> 135
		 *	eg:
	     *
	     * 2进制简单计算技巧:
	     * 	 1  0   0  1 0  0  0 0
	     * 	128 64 32 16 8  4  2 0
Integer.parseInt()
将10进制字符串转换为2进制整数 int

Integr.toString()
将2进制数字 int 转换为10进制字符串给人看

总结:
Java 能够处理10进制全部依赖于Integer类

代码块:

for (int i = 0; i <= 150; i++) {
       System.out.println(
       Integer.toBinaryString(i)
    );
}

16进制

16进制用于缩写 (简写) 2进制

2进制书写繁琐, 复杂, 易错; 由于16进制的基数是
2的4次幂,所以16进制可以实现2进制的缩写,其中
每4位2进制可以缩写为1位16进制;

如何缩写?
从2进制最低位开始, 每4位2进制可以缩写为1位16进制数字

     * 2进制与16进制
     * Java 7 支持直接书写2进制字面量, 以0b开头
     * Java 7 支持直接书写16进制字面量, 以0X开头
     * 0000     0             0111 1001 1101 1111 0110 1011 0010 1011  79DF6B2B
     * 0001     1              7     9    D    F    6    B    2    B
     * 0010     2             1011 0010 1101 0110 0010 1101 0110 1110  B2D62D6E
     * 0011     3               B    2    D    6   2     D    6    E
     * 0100     4             1011 1010 1110 1110 0001 1011 0101 1101  BAEE1B5D
     * 0101     5               B   A    E    E    1    B     5    D
     * 0110     6             1101 1011 1100 0111 0000 0111 1011 0110  DBC707B6
     * 0111     7               D   B    C    7     0    7   B    6
     * 1000     8             1001 1110 0110 0011 1100 1011 0110 1010  9E63CB6A
     * 1001     9               9    E    6    3    C    B    6    A
     * 1010     A             1011 1100 1001 1001 0110 1010 1110 1010  BC996AEA
     * 1011     B               B    C    9    9    6    A    E    A
     * 1100     C             1011 0101 0100 0011 1111 0100 1111 0111  B543F4F7
     * 1101     D               B    5    4    3    F    4    F    7
     * 1110     E             0110 1011 1011 1001 1110 1000 1001 0010  6BB9E892
     * 1111     F               6    B    B    9    E    8    9    2

代码块:

@Test
public void test01() throws Exception{
   int num = 0X6BB9E892;
   System.out.println(
           Integer.toBinaryString(num)
   );
}

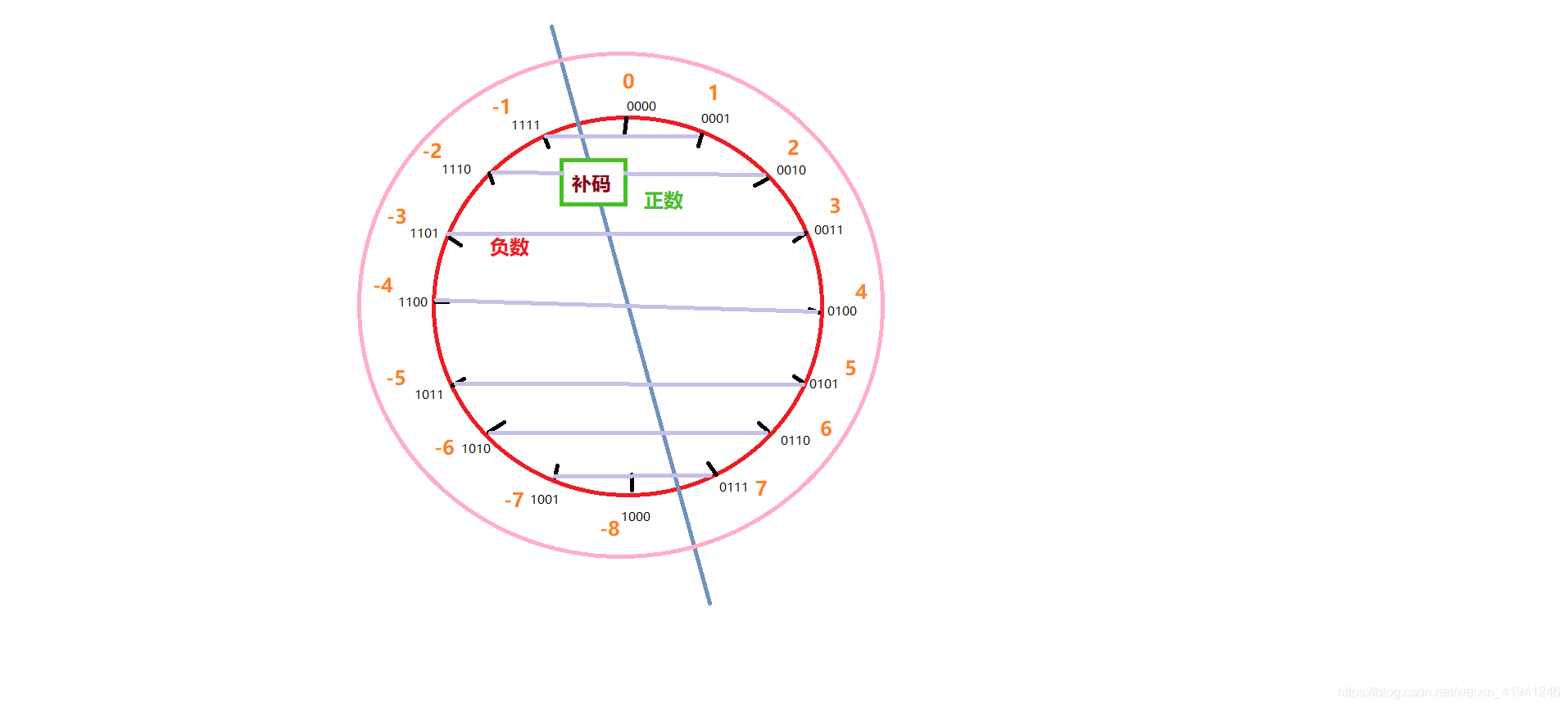
补码

什么是补码

计算机中用于处理负数的一种编码规则, 其核心思想是将固定位数

以4位2进制为例子讲解编码规则:

计算时候保持4位数不变, 超出的4位数的数据自动溢出, 不要了;
高位为0的一半作为正数, 高位为1的一半作为负数;
计算时候, 将10进制数 (包含负数) 转换为底层2进制补码计算,
计算结果也是2进制补码, 再利用 API 转换为10进制 (包含负数) 显示;
补码是环形编码, 最大值和最小值相接, 相差1
(巧合) 正数编码和负数编码互补对称, 故称为: 补码
计算补码的简单技巧

11111111111111111111111111101110
0000000000000000000000010001
0000000000000000000000010010

2进制取反代码块:

int num = -18;
int num02 = ~num + 1;

System.out.println(
        Integer.toBinaryString(num)
);// 11111111111111111111111111101110
System.out.println(
        Integer.toBinaryString(~num)
);// 00000000000000000000000000010001
System.out.println(
        Integer.toBinaryString(~num + 1)
);// 00000000000000000000000000010010

 int / long 负数的编码的算法技巧
 -(...  8 4 2 2)
 1 0 0 1 - - - >(-7)
int > -1 > (11111111111111111111111111111111)
 11111111111111111111111111101110 - - - > -18  > (num)  
 00000000000000000000000010001 - - - > 17  >(~num)
 00000000000000000000000010010  - - - > 18 >(~num+1)

运算符

运算规则 (逻辑乘法): 有0则0
0 & 0 = 0
0 & 1 = 0
1 & 0 = 0
1 & 1 = 1

约定: 将两个2进制数数字对齐, 应位子上的数字进行与运算
举个例子:
b: bit
1int = 8byte=32bit
--------- b1 ---------- b2 -------- b3 -------- b4 ------
n = 10101010 11110101 10101010 11001111
m = 00000000 00000000 00000000 11111111 ------->掩码(Mask 面具)
b4 = n&m = 00000000 00000000 00000000 1101111
如上案例, 是掩码计算: 其结果k中存储的数据是数字n的最后8位数
案例:
int n = 0xaaf5aacf;
int m = 0xff;
int b4 = n & m;

16进制代码块:

 @Test
    public void test03() throws Exception {
        /**
         * 10101010 11110101 10101010 11001111
         * 00000000 00000000 00000000 11111111
         * 00000000 00000000 00000000 11001111
         *
         */
        int n = 0xaaf5aacf;
        int m = 0xff;
        int b4 = n & m;
        System.out.println(
                Integer.toBinaryString(n)
        );
        System.out.println(
                Integer.toBinaryString(m)
        );
        System.out.println(
                Integer.toBinaryString(b4)
        );
    }

16进制 Result:

10101010111101011010101011001111
11111111
11001111

>>> 右移位运算

运算规则:

* 将数字的每个位向左侧移动, 移动后左侧多出的位自动溢出 (舍弃), 右侧补充0
* 例子:                                b1      b2       b3       b4                                                     
* n =                              01001111 10100110 11110001 10011110
* m = n >>> 1                      001001111 10100110 11110001 1001111 (0) 舍弃
* k = n >>> 2                      0001001111 10100110 11110001 100111 (10) 舍弃
* b1 = (n >>> 24) & 0xff;          00000000 00000000 00000000 01001111 (10100110 11110001 10011110)舍弃
* b2 = (n >>> 16) & 0xff;          00000000 00000000 00000000 10100110 (11110001 10011110)舍弃
* b3 = (n >>> 8) & 0xff;           00000000 00000000 00000000 11110001 (10011110)舍弃
* b4 = n & 0xff;                   00000000 00000000 00000000 10011110

 或运算 '|' 
 基本规则:逻辑加法, 有1则1 
 0 | 0 = 0
 0 | 1 = 1
 1 | 0 = 1
 1 | 1 = 1

左移位计算底层实现原理

将两个2进制数对齐位置, 对应的位置计算 "或"
举个例子:
n =        00000000 00000000 00000000 11011101
m =        00000000 00000000 11011101 00000000
k = n |m   00000000 00000000 11011101 11011101 

b1 = 00000000 00000000 00000000 01001111
b2 = 00000000 00000000 00000000 10100110
b3 = 00000000 00000000 00000000 11110001
b4 = 00000000 00000000 00000000 10011110

(b1 << 24) 01001111 00000000 00000000 00000000 
(b2 << 16) 00000000 10100110 00000000 00000000 
(b3 << 8)  00000000 00000000 11110001 00000000
b4         00000000 00000000 00000000 10011110

n = (b1 << 24) | (b2 << 16) | (b3 << 8) | b4;
       b1       b2       b3       b4         
n = 01001111 10100110 11110001 10011110
b1 = 0x4f;
b2 = 0xa6;
b3 = 0xf1;
b4 = 0x9e;
n = 0x4fa6f19e;

如上运算的意义: m和n两个拼接以后为k
案例:
int n = 0xdd;
int m = 0xdd00;
int k = n | m;

左移位计算代码块:

 @Test
    public void test05() throws Exception {
        int b1 = 0x4f << 24;
        int b2 = 0xa6 << 16;
        int b3 = 0xf1 << 8;
        int b4 = 0x9e;

        int n = b1 | b2 | b3 | b4;// n = 0x4fa6f19e;

        System.out.println(
                Integer.toBinaryString(n)
        );// 01001111 10100110 11110001 10011110

        System.out.println(
                Integer.toBinaryString(b1)
        );// 01001111

        System.out.println(
                Integer.toBinaryString(b2)
        );// 10100110

        System.out.println(
                Integer.toBinaryString(b3)
        );// 11110001

        System.out.println(
                Integer.toBinaryString(b4)
        );// 10011110

    }

左移位计算 Result:

01001111 10100110 11110001 10011110
10011110 00000000000000000000000
10100110 0000000000000000
11110001 00000000
10011110

位移计算的数学意义

10进制左移动小数点计算: 
//    	  18319.
// 	     183190. 扩大10倍
//	   18319100. 扩大100倍

如果小数点不动, 数字向左移动一次, 扩大10倍

2进制左移位小数点计算:
//        110010.	50
//		 1100100.	100    扩大2倍
//      11001000.   200    扩大4倍
如果小数点不动, 数字向左移动一次, 扩大2倍

2进制右移位小数点计算:
//        11001.	25     缩小2倍
//         1100.	12     缩小4倍, 小方向取整数


案例:
int n = 50;
int m = n << 1;	100	// 扩大2倍
int k = n << 2;	200	// 扩大4倍
int o = n >> 1;	25	// 缩小2倍
int p = n >> 2;	12	// 缩小4倍

>>> 和 >> 的区别
'>>>' 逻辑右移位: 将2进制数字向右移位, 低位自动溢出舍弃, 高位补0
'>>' 数学右移位: 将2进制数字向右移位, 低位自动溢出舍弃,正数补0, 负数补1

举个例子:
n = -50                 11111111 11111111 11111111 11001110             -50
m = n >> 1              111111111 11111111 11111111 1100111 (0)舍弃     -25
k = n >> 2              1111111111 11111111 11111111 110011 (10)舍弃    -13 小方向取整数
g = n >>> 1             011111111 11111111 11111111 1100111(0)舍弃      比最大值少24

案例:
int n = -50;     -50
int m = n >> 1;  -25
int k = n >> 2;  -13 小方向取整数
int g = n >>> 1; 比最大值少24

如上结果说明:
 '>>' : 计算是数学除法
'>>>' : 不是数学除法, 就是逻辑上将数组向右移动, 不区分正负数;

向右移动有符号问题, 所以有两个运算符号, 左移动只有一个符号 '<<'

使用建议: 
如果替代除法(2的整数幂) : '>>'
如果是拆分数据, 就是实现数位的移动 : '>>>'

经典面试题: 
n * 16 可以替换为 (n << 4) (16 = 2^4)
size / 2 (size > 0)  可以替换为 (size >> 1)