Gym 100814A Arcade Game (STL排列组合+二项式定理)

最新推荐文章于 2021-03-16 20:16:52 发布

lero1005

最新推荐文章于 2021-03-16 20:16:52 发布

阅读量310

点赞数

CC 4.0 BY-SA版权

分类专栏：算法学习

本文链接：https://blog.youkuaiyun.com/weixin_41934068/article/details/81812855

算法学习专栏收录该内容

36 篇文章

订阅专栏

本文介绍了一道算法题目 Gym100814A 的解题思路与实现方法。该题要求计算从给定数字通过特定规则达到最大全排列数字的概率。文中详细解释了如何利用 C++ 中的 next_permutation 函数来确定最大距离，并通过二项式定理计算最终的概率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Gym 100814A

题意：给定数字n(1 ≤ n ≤ 1e9)，n由0,1,2,3,4,5,6,7,8,9组成，第一位不为0且无重复数字。每一步都可以由当前的数字跳转到由n中数字全排列构成的数字，当跳转到比n小的数字时，游戏结束，当跳转到全排列后最大的数字，游戏胜利。

问：有多大的概率可以胜利。

解：

假设给定数字为num，通过%、/操作可以取出num中的每一位数字，假设num有n位。

我们知道，n位数字可以构成（n！）个数字，所以每一步共有（n！）个选择，即选中任意一个数字的的概率为1/(n！)，如果想要获胜，那么我们就要一直选比num大的数字，直到选中（n！）个数字中最大的数为止。

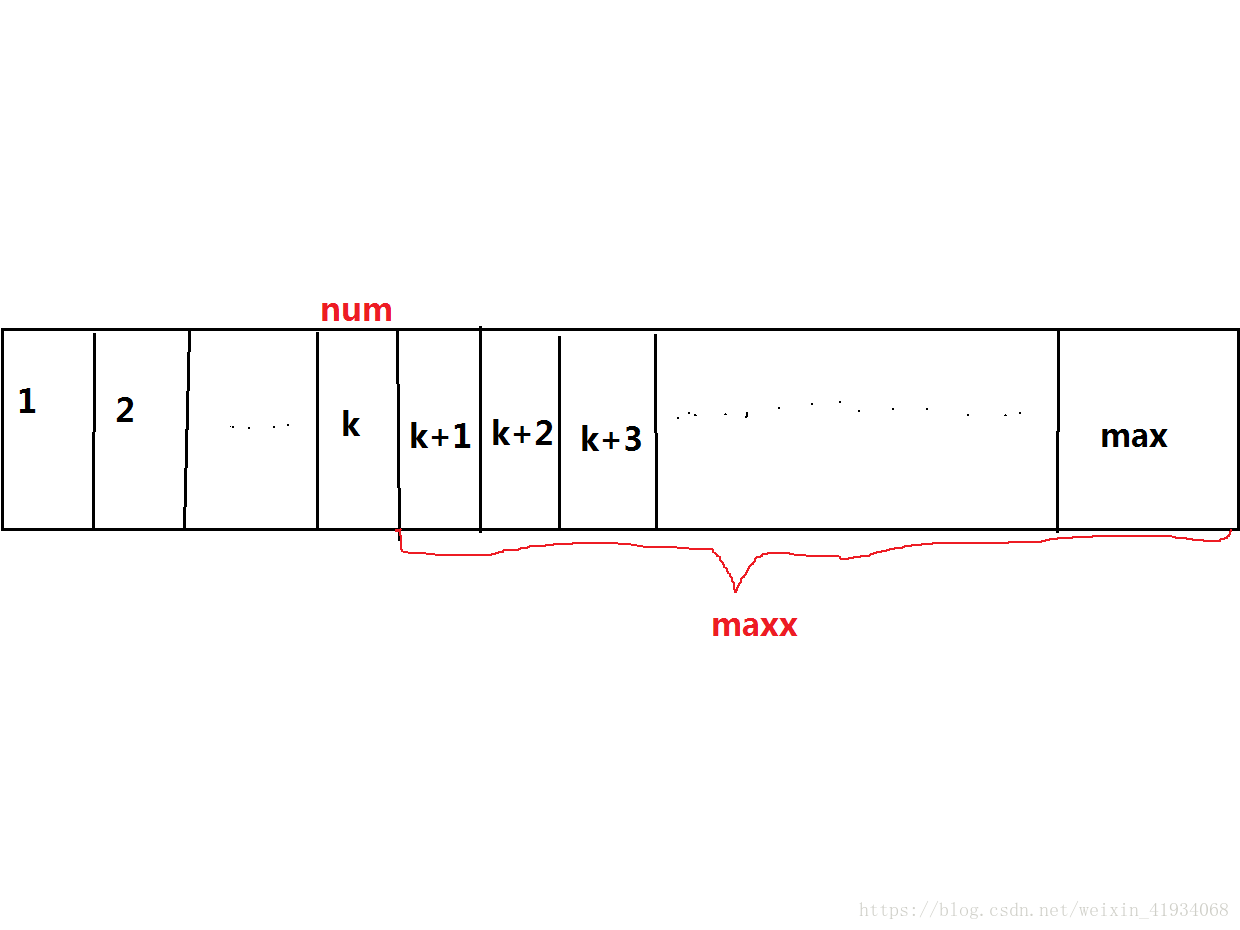
如图，因为想要胜利，每一步都要到达比现在所处的数更大的数，且终点为max。

C++的函数库里自带的next_permutation(a,a+n)讲返回由数组中元素全排列构成的比当前数组中排列更大的一个数（字典序），所以我们可以知道max与当前数字的距离maxx。

我们设 pr = 1/(n!)：

到达maxx，关键在于几步到达，一步到达maxx的概率为pr，两步到达的概率为 $\binom{maxx}{1}$ * $pr^{2}$ , k步到达的概率为 $\binom{maxx}{k-1}$ $pr^{k}$ ……

这样，我们很容易地（使劲看能看出来）想到了二项式定理： $(x+y)^{n} = \sum \binom{n}{k}*x^{k}*y^{n-k}$ ，所以本题的答案其实就是 $(1+pr)^{maxx-1} * pr$ .

AC代码如下：

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <cmath>
using namespace std;
const int maxn =4e6;
const int INF  =1e9;
int main()
{
    int N;
    while(scanf("%d",&N) != EOF)
    {
        while(N--)
        {
        int a[15];
        int maxx = 0;
        int num,n = 0;
        cin>>num;
        int t = num;
        int flag = 0;
        while(t)
        {
            a[n++] = t%10;
            t /= 10;
        }
        //cout<<"n = "<<n<<endl;
        reverse(a,a+n);
        while (next_permutation(a,a+n))
        {
                maxx++;
        }
        //cout<<maxx<<endl;
        double ans = 0;
        if(maxx != 0)
        {
            double pr = 1;
            for(int i = 1; i<=n; i++)
                pr *= i;
            pr = 1/pr;
            ans = pow(1+pr,maxx-1) * pr;
        }
        printf("%.9f\n",ans);
        }
    }
    return 0;
}