一些变量筛选方法——3、部分其它变量筛选方法

由于《An Introduction to Statistical Learning with R》书中的方法书中的方法都是一些比较基础的方法，在做模拟实验以及真实超高维数据时，会出现很多局限性。因此本文后半部分介绍了课本上未提及到的一些方法。这些方法会在后面的模拟实验以及真实数据中进行应用，并且比较书上传统的方法与下述三种方法的真实变量筛选效果。

首先介绍将$L^0$范数与$L^1$范数相结合的SCAD方法。

---

SCAD(Smoothly Clipped Absolute Deviation)

与岭回归相比，SCAD降低了模型的预测方差，与此同时与Lasso相比，SCAD又缩小了参数估计的偏差，同时它还有很多前面算法所不具备的优秀性质，因而受到了广泛的关注。

SCAD将前面博客提到的$g_{\lambda }(\beta )=\lambda f(\beta )$，变为如下形式：
$$g_{\lambda }(\beta )=\{\begin{array}{ll}\lambda |{\beta }_j|,& 0\le |{\beta }_j|<\lambda ,\\ -(|{\beta }_j{|}^2-2a\lambda |{\beta }_j|+{\lambda }^2)/(2a-2),& \lambda \le |{\beta }_j|<a\lambda ,\\ (a+1){\lambda }^2/2,& |{\beta }_j|\ge a\lambda .\end{array}$$

其中，$\lambda \ge 0,a>2$，Fan和Li\cite{article11} 建议a取3.7。特别地，若设计矩阵$X$正交时，SCAD法参数估计显式表达式如下：
$${\hat{\beta }}^{SCAD}=\{\begin{array}{ll}sign(\widehat{{\beta }_j})|\widehat{{\beta }_j}|-\lambda ),& 0\le |{\beta }_j|<2\lambda ,\\ ((a-1)\widehat{{\beta }_j}-sign(\widehat{{\beta }_j})a\lambda )/(a-2),& 2\lambda \le |\widehat{{\beta }_j}|<a\lambda ,\\ \widehat{{\beta }_j},& |\widehat{{\beta }_j}|\ge a\lambda .\end{array}$$

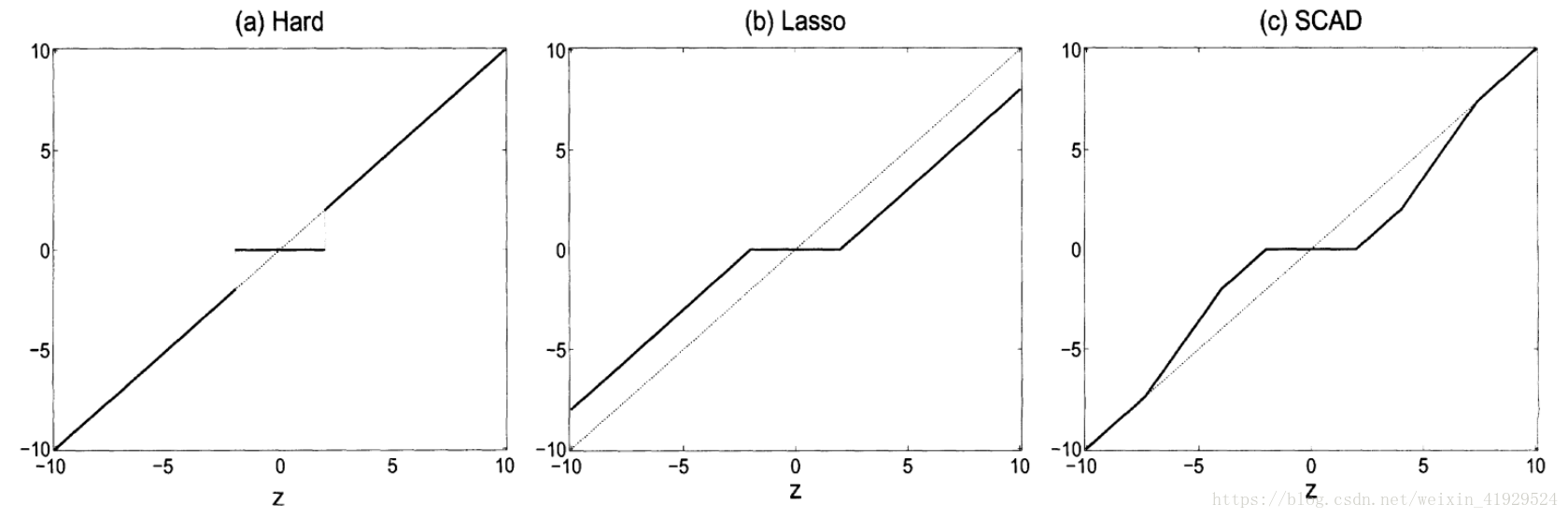
上图说明了$L^0$惩罚，$L^1$惩罚，与SCAD三者惩罚之间的差别。可以看出，$L^0$方法只会进行变量筛选，不会进行压缩，$L^1$（LASSO）既会进行变量筛选，也会对系数继续一定的调整。而SCAD可以从图中很明显的其结合了两种方法，对系数较大的变量不进行惩罚，对系数较少的进行压缩或者删去，因此这种方法既可以筛选变量，也有着Oracle的性质，使其预测效果和真实模型别无二致。

SCAD虽然有相应的迭代算法，但是由于其复杂度高，所以计算速度相对较慢。另外老师上课讲过的将$L^1$与$L^2$范数相结合的Elastic Net方法\cite{article16}，也是基于前面的一种衍生方法，本文不再进行阐述。

---

SIS（Sure Independence Screening）

当今大数据时代，维数远大于样本量的情况已经非常多见。尽管前面所提出的方法，而且也能一定程度上解决髙维数据问题。但当遇到超高维数据，即维数P无穷大时，上述的算法也会出现问题。针对这类超高维问题，Fan和Lv\cite{article12} 提出了SIS的方法。

针对线性回归模型(2)，按照SIS的思想，首先$Y$为中心化向量，计算$Y$与每一个自变量$x_i$的相关系数，记为
$$\omega =X^{T}Y,$$
其中 $\omega =({\omega }_1,\cdots ,{\omega }_p{)}^T$,若${\omega }_i$越大，说明$x_i$与$Y$相关性越强。所以，可以根据$|{\omega }_i|$的大小来进行变量选择。对任意的$\gamma \in (0,1)$，对$|{\omega }_i|$进行从大到小排序，然后取其一个子集

M γ = { 1 ≤ i ≤ p : ∣ ω i ∣ 是前 [ γ n ] 个最大的 } , M_\gamma = \lbrace 1 \leq i \leq p:|\omega_i| \text{是前}[\gamma n] \text{个最大的} \rbrace, Mγ​={1≤i≤p:∣ωi​∣是前[γn]个最大的},

其中，$n$是样本数，$[\gamma n]$是$\gamma n$的整数部分，进而保证了$[\gamma n]<n$，与之对应的自变量则入选模型。如果觉得选择$[\gamma n]$不便于确定，可以选择$n-1$或$n/\log n$。

而关于相关系数，可以选用自己认为合适的。本文后面的模拟选用传统的Pearson相关系数，以及近几年比较火的可用于检验独立的无参数假设的距离相关性（Distance Covariance），下面其计算公式：

距离相关性（Distance Covariance）

$$\begin{array}{rl}{a}_{j,k}& =\Vert X_j-X_k\Vert ,j,k=1,2,\dots ,n,\\ b_{j,k}& =\Vert Y_j-Y_k\Vert ,j,k=1,2,\dots ,n,\end{array}$$
其中：$||\cdot ||$表示Euclidean范数（欧几里得距离），有：
$$A_{j,k}:=a_{j,k}-{\overline{a}}_{j\cdot }-{\overline{a}}_{\cdot k}+{\overline{a}}_{\cdot \cdot },B_{j,k}:=b_{j,k}-{\overline{b}}_{j\cdot }-{\overline{b}}_{\cdot k}+{\overline{b}}_{\cdot \cdot },$$

其中：${\overline{a}}_{j\cdot }$表示由$a_{j,k}$组成的矩阵，第$j$行均值，${\overline{a}}_{\cdot k}$ 表示第$k$列均值，以及${\overline{a}}_{\cdot \cdot }$是$X$样本中所有数取平均。$b$的符号标记同$a$一样，则样本的距离相关性定义为：
$${\text{dCov}}_n^2(X,Y):=\frac{1}{n^2}\sum _{j=1}^n\sum _{k=1}^n{A}_{j,k}{B}_{j,k}.$$

---

利用随机森林进行变量筛选

其实使用随机森林进行变量筛选是一个比较小众的方法，但其实代表了一类方法。模型本身是用于预测的模型，但在预测过程中，可以对变量重要性进行排序，然后通过这种排序来进行变量筛选。这类方法其实还适用于最近比较火的xgboost，lightgbm等一些非常流行的基于树的机器学习算法，在实际应用中，效果都非常突出。

本文只以较为基础的随机森林中的变量筛选为例：

变量重要性评判用Gini指数为标准，针对一棵树中的每个节点$k$，我们都可以计算一个Gini指数：
$$G_k=2{\hat{p}}_k(1-{\hat{p}}_k),$$
其中${\hat{p}}_k$表示样本在节点$k$属于任意一类的概率估计值。

一个节点的重要性由节点分裂前后Gini指数的变化量来确定：
$$I_{△k}=G_k-G_{k1}-G_{k2},$$
$G_{k1}$和$G_{k2}$分别表示$G_k$产生的子节点。针对森林中的每棵树，都用上述的标准来递归产生，最终随机抽取样本和变量，产生森林，假设森林共产生$T$棵树。

森林中，如果变量$X_i$在第$t$棵树中出现$M$次，则变量$X_i$在第$t$棵树的重要性为：
$$I_{it}=\sum _{j=1}^M{I}_{△j}.$$

则$X_i$在整个森林中的变量重要性为：
$$I_{(i)}=\frac{1}{n}\sum _{t=1}^T{I}_{it}.$$

最终我们根据变量重要性来选择变量，选择的个数可以用SIS中的方法，选取$n-1$或$n/\log n$个。

至此，变量筛选的一些方法已进行了简要的概述，包括课本中的以及一些延伸的方法。下面将用模拟实验以及真实数据，来对这些方法进行比较分析。

---

原始对偶激活集算法(PDAS)

原始对偶激活集算法（Primal Dual Active Set，PDAS）是一个非常新的方法，但做的事情是最优子集选择的事情。其主要思想是引入激活集，对所有的$\beta$进行批量迭代更新。这个方法的优势在于，可以处理超高维数据（上万维），而最优子集选择一旦超过了50维，基本就完全没办法进行运算。后面我们也将采用PDAS来进行模拟。

其算法如下：

1. 给定某固定的$T$，初始的${\beta }^0$，$d^0=-\frac{g({\beta }_0)}{h({\beta }_0)}$，根据${\beta }^0$和$d^0$得出${\mathcal{A}}^0$、${\mathcal{I}}^0$。令$k=0$

2. For $k=0,1,2,\dots ,K_{max}$, do
   (2.a) 更新$({\beta }^{k+1},d^{k+1})$:
   $$\{\begin{array}{l}{\beta }_{I^k}^{k+1}=0\\ d_{A^k}^{k+1}=0\\ {\beta }_{A^k}^{k+1}=argminl({\beta }_{A^k}|\text{Y},{\text{X}}_{A^k})\\ d_{I^k}^{k+1}=-\frac{g({\beta }_{I^k}^k)}{h({\beta }_{I^k}^k)}\end{array}$$
   (2.b) 通过以下方式计算新的激活集${\mathcal{A}}^{k+1}$和非激活集${\mathcal{I}}^{k+1}$:
   A k + 1 = { j : − h ( β j k + 1 ) ∣ β j k + 1 + d j k + 1 ∣ ⩾ − h ( β j k + 1 ) ∥ β j k + 1 + d j k + 1 ∥ T , ∞ } , A^{k+1}=\lbrace{j}:\sqrt{-h(\beta_{j}^{k+1})}\vert\beta_{j}^{k+1}+d_{j}^{k+1}\vert\geqslant\sqrt{-h(\beta_{j}^{k+1})}\Vert\beta_{j}^{k+1}+d_{j}^{k+1}\Vert_{T,\infty}\rbrace, Ak+1={j:−h(βjk+1​) ​∣βjk+1​+djk+1​∣⩾−h(βjk+1​) ​∥βjk+1​+djk+1​∥T,∞​},
   $$I^{k+1}=(A^{k+1}{)}^c$$
   (2.c) 如果${\mathcal{A}}^{k+1}={\mathcal{A}}^k$，则停止迭代；否则令$k=k+1$，继续(2.a)和(2.b)步。
   (2.d) 输出$\beta ={\beta }^{k+1}$。

---

后面我们将对前面提及的一些算法进行模拟，以及真实案例操作。传送门：一些变量筛选方法——4、模拟实验