数据结构与算法之复杂度分析篇(下)

一、内容

        最好情况时间复杂度、最坏情况时间复杂度、平均情况时间复杂度、均摊时间复杂度。

二、为什么要引入这几个概念？

        有助于我们可以更加全面地表示一段代码的执行效率，同样一段代码，在不同的输入情况下，复杂度量级有可能是不一样的情况。

三、最好、最坏情况时间复杂度

         (1)、最好情况时间复杂度：在理想情况下，执行这段代码的时间复杂度；

         (2)、最坏情况时间复杂度：在最糟糕的情况下，执行这段代码的时间复杂度；

         举例说明：

最好情况时间复杂度：如果数组中第一个元素正好是要查找的变量X，那就不需要继续遍历剩下的n-1个数据了，那时间复杂度就是O(1)；

           最坏情况时间复杂度：如果数组中不存在变量X，那我们就需要把整个数组都遍历一遍，时间复杂度就成了O(n)。

四、平均情况时间复杂度

          引用上面的例子来说明，我们知道要查找的变量X，要么就不再数组里。这两种情况对应的概率统计起来很麻烦，为了方便你理解，我们假设在数组中与不在数组中的概率都为1/2。另外，要查找的数据出现在0~n-1这n个位置的概率也是一样的，为1/n。所以，根据乘法法则，要查找的数据出现在0~n-1中任意位置的概率就是1/(2n)。

        因此，平均时间复杂度的计算过程就变成了这样：

          

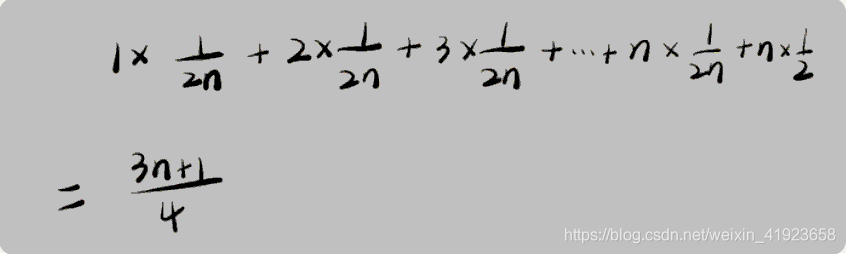
        这个值就是概率论中的加权平均值，也叫做期望值，所以平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度。

       引入概率之后，前面那段代码的加权平均值为(3n+1)/4。用大O来表示，去掉系数和常量，这段代码 的加权平均时间复杂度仍然是O(n)。

 五、均摊时间复杂度

       均摊时间复杂度，听起来跟平均时间复杂度有点儿像。对于初学者来说，这两个概念确实非常容易弄混。但大部分情况下，我们并不需要区分最好、最坏、平均三种复杂度。平均复杂度只在某些特殊情况下才会用到，而均摊时间复杂度应用的场景比它更加特殊、更加有

         (1)、 应用场景：

        对一个数据结构进行一组连续操作中，大部分情况下时间复杂度都很低，只有在个别情况下时间复杂度比较高，而且这些操作之间存在前后连贯的时序关系，这个时候，我们就可以将这一组操作放在一块儿分析，看是否能将较高时间复杂度那次操作的耗时，平摊到其他那些时间复杂度比较低的操作上。而且，在能够应用均摊时间复杂度分析的场合，一般均摊时间复杂度就等于最好情况时间复杂度。

       (2)、 分析方法：

                 摊还分析法；

          举例说明

         这段代码实现了一个往数组中插入数据的功能。当数组满了之后，也就是代码中count==array.length时，我们用for循环遍历数组求和，并清空数组，将求和之后的sum值放到数组的第一个位置，然后再将新的数据插入数组。

          由前面的知识可知，数组中有空闲时间，我们只需将数据插入到数组下标为count的位置就可以了，所以最好情况时间复杂度为O(1)。最坏的情况下，数组中没有空闲时间了，我们需要先做一次数组的遍历求和，然后再将数据插入，所以最坏情况时间复杂度为O(n)。

         对于平均时间复杂度，我们可以通过前面讲的概率论的方法来分析。

       假设数组的长度是n，根据插入的位置不同，我们可以分为n种情况，每种情况的时间复杂度是O(1)。 除此之外，还有一种"额外"的情况，就是在数组没有空闲时间时插入一个数据，这个时候的时间复杂度是O(n)。而且，这n+1种情况发生的概率一样，都是1/(n+1)。所以，根据加权平均的计算方法，我们求得的平均时间复杂度就是：

       

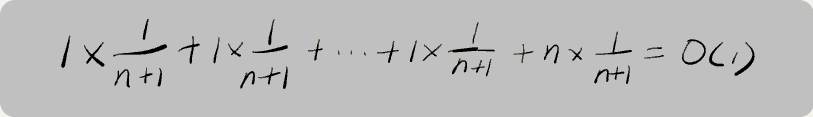
      课后思考题：

          分析下面add()函数的时间复杂度。

               最好情况时间复杂度:O(1);

               最坏情况时间复杂度:O(n);

               均摊时间复杂度:O(1);   个人理解：对于add()函数，大部分情况下的时间复杂度为O(1)；极端情况下的时间复杂度为O(n),平摊到时间复杂度为O(1)的操作上，最终平均时间复杂度为O(1);其实个人觉得当大部分情况下为O(1),那么平均时间复杂度为O(1)。在能够应用均摊时间复杂度分析的场合，一般均摊时间复杂度就等于最好情况时间复杂度。

---

扫码关注微信公众号，欢迎技术交流，其中含有大量免费的人工智能、图像处理、IT资料：