【POJ 2318】TOYS

最新推荐文章于 2021-05-12 20:50:00 发布

原创最新推荐文章于 2021-05-12 20:50:00 发布 · 230 阅读

0 ·

CC 4.0 BY-SA版权

计算几何专栏收录该内容

11 篇文章

订阅专栏

博客围绕一道几何基础题展开，题目是矩形盒子被n条线段分割成不同区域，给出m个点坐标，需输出各区域落点数量。分析指出若点p在向量AB左边，PA叉乘PB为负，可由右手定则解释，且具有单调性，可通过二分确定位置。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.题目链接。题目大意就是有一个矩形的盒子，里面被n条线段分割成了几个不同的区域，然后给出m个点的左边，输出一下每个区域里面格子落了多少个点。

2.分析:几何的基础题了

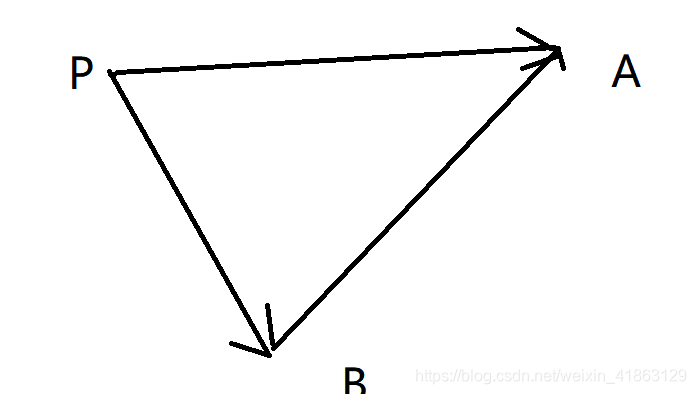
如果p在向量AB的左边，那么PA叉乘PB是一个负数，右手定则轻松解释。然后这个是具有单调性的，所以我们直接二分这个位置就行了。

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
#include <map>
#include <vector>
#include <set>
#include <string>
#include <math.h>
#pragma warning(disable:4996)
using namespace std;
struct Point
{
	int  x, y;
	Point() {};
	Point(int  x_, int  y_) :x(x_), y(y_) {};
	Point operator-(const Point&b)const
	{
		return Point(x - b.x, y - b.y);
	}
	int   operator*(const Point&b)const
	{
		return x * b.x + y * b.y;
	}
	int  operator^(const Point&b)const
	{
		return x * b.y - y * b.x;
	}
};
struct Line
{
	Point s, e;
	Line() {};
	Line(Point _s, Point _e ): s(_s), e(_e){};
};
int xmult(Point p0, Point p1, Point p2)
{
	return (p1 - p0) ^ (p2 - p0);
}
const int MAXN = 5050;
Line line[MAXN];
int ans[MAXN];
int main()
{
	int n, m;
	int x1, y1, x2, y2;
	bool f = 1;
	while (~scanf("%d", &n) && n)
	{
		if (f)f = 0;
		else puts("");
		scanf("%d%d%d%d%d", &m, &x1, &y1, &x2, &y2);
		int Ui, Li;
		for (int i = 0; i < n; i++)
		{
			scanf("%d%d", &Ui, &Li);
			line[i] = Line(Point(Ui, y1), Point(Li, y2));
		}
		line[n] = Line(Point(x2, y1), Point(x2, y2));
		int x, y;
		Point p;
		memset(ans, 0, sizeof(ans));
		while (m--)
		{
			scanf("%d%d", &x, &y);
			p = Point(x, y);
			int l = 0, r = n;
			int tmp;
			while (l <= r)
			{
				int mid = (l + r) >> 1;
				if (xmult(p, line[mid].s, line[mid].e) < 0)
				{
					tmp = mid;
					r = mid - 1;
				}
				else l = mid + 1;
			}
			ans[tmp]++;
		}
		for (int i = 0; i <= n; i++)
			printf("%d: %d\n", i, ans[i]);
	}
	return 0;
}