机器学习实战之逻辑回归logestic regression

机器学习实战这本书最大的缺点就是对代码注释的不够详细，尤其是很多运算过程直接省略。

最起码应该在开始代码前先将主要的数学结论说清楚。

逻辑回归logestic regression，

回归：指研究一组随机变量(Y1 ，Y2 ，…，Yi)和另一组(X1，X2，…，Xk)变量之间关系的统计分析方法

关系符合线性的叫线性回归，符合逻辑函数关系的叫逻辑回归。

这里用逻辑回归处理一些非线性的分类问题。

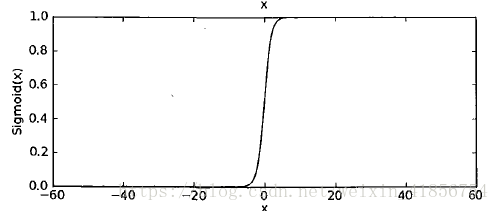
用到的函数sigmoid：近似一种阶跃函数，大于0.5归为1，小于0.5归为0；0.5作为分割线，

也可以指定别的值作为分割线。

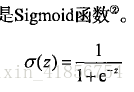
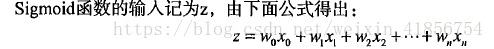
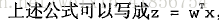
这里涉及到矩阵乘法，矩阵相乘只有前列数和后行数一致才有意义，

得到一个前行后列的新矩阵。T表示矩阵的转置，行列互换。

w是回归系数向量，x是数据向量。

回归的目的就是为了求得最佳回归系数w，最佳回归系数可以用来测试新数据的分类。

最佳回归系数w符合其似然函数函数f(w)的最大值：

经过一系列的运算：f(w)对w的求导可以求得：

df(w)/dw=x*error

error是误差：error=y-sigmoid(z),就是error=y-sigmoid(w*x)

数据乘以回归系数后与实际分类值的误差。

为了求得f(w)的最大值，用到一种最优化算法：梯度上升算法，

还有梯度下降算法，可以求一个函数的最小值，比如最小二乘法的求解？不太懂，慢慢理解。

梯度上升算法的迭代公式：

w=w+step*df(w)/dw

step是步长值，可以自己设定，比如0.01；

在随机梯度算法中设定为动态的：step=0.01+4/（1.0+迭代次数n），随着迭代次数增多趋近于0.01；

其中：df(w)/dw称为梯度

根据上面已经算出的df(w)/dw=x*error

可得到：

w=w+step*x*error

# -*- coding: cp936 -*-
#logistics Regression,逻辑回归
#回归，指研究一组随机变量(Y1 ，Y2 ，…，Yi)和
#另一组(X1，X2，…，Xk)变量之间关系的统计分析方法
#最简单的情形是一元线性回归，由大体上有线性关系的一个自变量和一个因变量组成；
#模型是Y=a+bX+ε（X是自变量，Y是因变量，ε是随机误差）。
#这里logistics回归用到Sigmoid函数，Sigmoid函数计算的是某个向量属于1的概率。
#一般以0.5为分割线，大于0.5则认为这个向量属于1。可由此求出分割线方程。
#1.0/（1+exp(-z)）=0.5
#z=0
#w0x0+w1x1+w2x2+...+wnxn=0


from numpy import *


def sigmoid(inX):
    return 1.0/(1+exp(-inX))
#sigmoid函数的输入记为z，即z=w0x0+w1x1+w2x2+...+wnxn，其中x0=1,w0表示常数项。
#如果用向量表示即为z=wTx，它表示将这两个数值向量对应元素相乘然后累加起来。
#其中，向量x是分类器的输入数据，
#w即为我们要拟合的最佳参数，从而使分类器预测更加准确。


def loadDataSet():
    dataMat=[]
    labelMat=[]
    fr=open(r'H:\study\python\machine learning\machinelearninginaction\Ch05\testSet.txt')
    for line in fr.readlines():
        lineArr=line.strip().split()
        dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])
        #testSet中，有三列数据，后一列是类标签。
        #处理的时候，多加了一列数据在最前面，都为1.0
        labelMat.append(int(lineArr[2]))


    return dataMat,labelMat




def gradAscent(dataMatIn,classLabels):
    #梯度上升，返回训练好的回归系数
    #最小化损失函数，就用梯度下降，最大化似然函数，就用梯度上升。