java第十一天---Scanner类及其方法，String类，StringBuffer类，数组高级算法（冒泡排序、选择排序、直接插入排序，快速排序，归并排序, 希尔排序,堆排序）

最新推荐文章于 2021-11-19 10:53:43 发布

原创最新推荐文章于 2021-11-19 10:53:43 发布 · 300 阅读

1 ·

CC 4.0 BY-SA版权

本文深入探讨Java中String与StringBuffer的特性及应用，覆盖构造方法、字符串操作、性能对比等内容，适合初学者及进阶开发者阅读。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1 Scanner的构造方法以及方法

Scanner(InputStream source)

hasNextXxx() 判断下一个是否是某种类型的元素,其中Xxx可以是Int,Double等。如果需要判断是否包含下一个字符串，则可以省略Xxx
nextXxx() 获取下一个输入项。Xxx的含义和上个方法中的Xxx相同

2 String

字符串字面值"abc"也可以看成是一个字符串对象。字符串是常量，一旦被创建，就不能被改变。因为字符串的值是在方法区的常量池中划分空间分配地址值的

A:常见构造方法
       public String():空构造
       public String(byte[] bytes):把字节数组转成字符串
       public String(byte[] bytes,int index,int length):把字节数组的一部分转成字符串(index:表示的是从第几个索引开始, length表示的是长度)
       public String(char[] value):把字符数组转成字符串
       public String(char[] value,int index,int count):把字符数组的一部分转成字符串
       public String(String original):把字符串常量值转成字符串

3 String的判断功能和获取功能和转换功能

判断功能

public boolean equals(Object obj):               比较字符串的内容是否相同,区分大小写
       public boolean equalsIgnoreCase(String str):       比较字符串的内容是否相同,忽略大小写
       public boolean contains(String str):               判断字符串中是否包含传递进来的字符串
       public boolean startsWith(String str):               判断字符串是否以传递进来的字符串开头
       public boolean endsWith(String str):               判断字符串是否以传递进来的字符串结尾
       public boolean isEmpty():                       判断字符串的内容是否为空串""。

获取功能

public int length():                           获取字符串的长度。
       public char charAt(int index):                   获取指定索引位置的字符
       public int indexOf(int ch):                       返回指定字符在此字符串中第一次出现处的索引。
       public int indexOf(String str):                   返回指定字符串在此字符串中第一次出现处的索引。
       public int indexOf(int ch,int fromIndex):           返回指定字符在此字符串中从指定位置后第一次出现处的索引。
       public int indexOf(String str,int fromIndex):       返回指定字符串在此字符串中从指定位置后第一次出现处的索引。

public String substring(int start): 从指定位置开始截取字符串,默认到末尾。
public String substring(int start,int end): 从指定位置开始到指定位置结束截取字符串。（包头不包尾）

转换功能

public byte[] getBytes():                       把字符串转换为字节数组。
       public char[] toCharArray():                   把字符串转换为字符数组。
       public static String valueOf(char[] chs):           把字符数组转成字符串。
       public static String valueOf(int i):               把int类型的数据转成字符串。
           注意：String类的valueOf方法可以把任意类型的数据转成字符串。
       public String toLowerCase():                   把字符串转成小写。
       public String toUpperCase():                   把字符串转成大写。
       public String concat(String str):                   把字符串拼接。

4 String的替换、去空格、比较功能

public String replace(char old,char new) 将指定字符进行互换
public String replace(String old,String new) 将指定字符串进行互换

public String trim() 去除两端空格

public int compareTo(String str) 会对照ASCII 码表从第一个字母进行减法运算返回的就是这个减法的结果，如果前面几个字母一样会根据两个字符串的长度进行减法运算返回的就是这个减法的结果，如果连个字符串一摸一样返回的就是0
public int compareToIgnoreCase(String str) 跟上面一样只是忽略大小写的比较

5 StringBuffer

StringBuffer类概述
我们如果对字符串进行拼接操作，每次拼接，都会构建一个新的String对象，既耗时，又浪费空间。而StringBuffer就可以解决这个问题. 线程安全的可变字符序列

StringBuffer和String的区别:

String 固定长度字符串，StringBuffer可变长度字符串

6 StringBuffer的构造方法以及方法

StringBuffer的构造方法：
       public StringBuffer():               无参构造方法
        public StringBuffer(int capacity):   指定容量的字符串缓冲区对象
        public StringBuffer(String str):       指定字符串内容的字符串缓冲区对象

StringBuffer的方法：
public int capacity()：返回当前容量。理论值
public int length():返回长度（字符数）。实际值

7 StringBuffer的添加、删除、替换、反转、截取功能

A:StringBuffer的添加功能
public StringBuffer append(String str): 可以把任意类型数据添加到字符串缓冲区里面,并返回字符串缓冲区本身
public StringBuffer insert(int offset,String str):在指定位置把任意类型的数据插入到字符串缓冲区里面,并返回字符串缓冲区本身

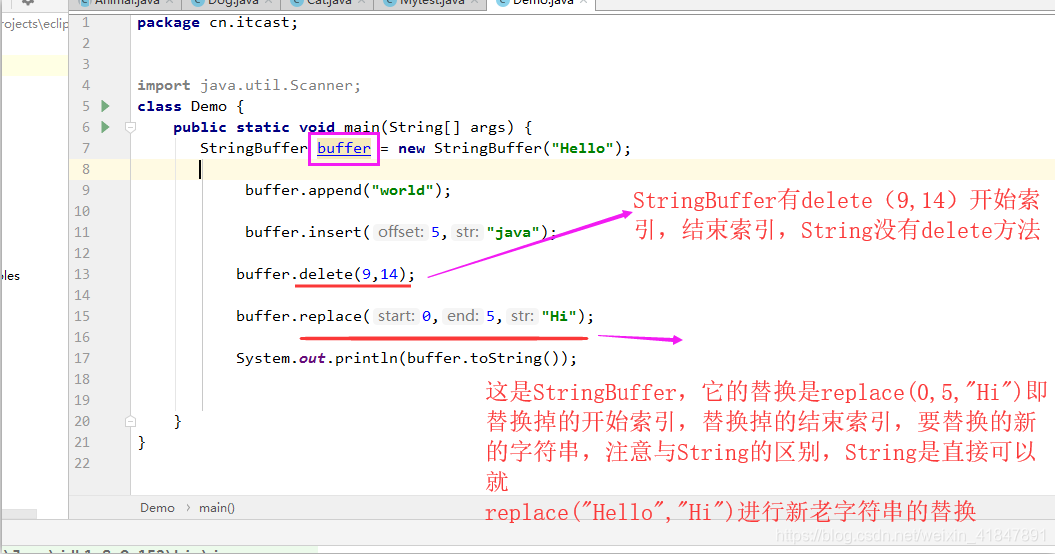
B:StringBuffer的删除功能
public StringBuffer deleteCharAt(int index):删除指定位置的字符，并返回本身
public StringBuffer delete(int start,int end):删除从指定位置开始指定位置结束的内容，并返回本身

C:StringBuffer的替换功能
public StringBuffer replace(int start,int end,String str): 从start开始到end用str替换
D:StringBuffer的反转功能
public StringBuffer reverse(): 字符串反转

E:StringBuffer的截取功能
public String substring(int start): 从指定位置截取到末尾
public String substring(int start,int end): 截取从指定位置开始到结束位置，包括开始位置，不包括结束位置

注意:截取功能substring返回值类型不再是StringBuffer本身,而是返回字符串类型.

8 String,StringBuffer,StringBuilder的区别

String 长度固定

StringBuffer 长度可变，线程安全

StringBuilder 长度可变，线程不安全

9 String和StringBuffer分别作为参数传递

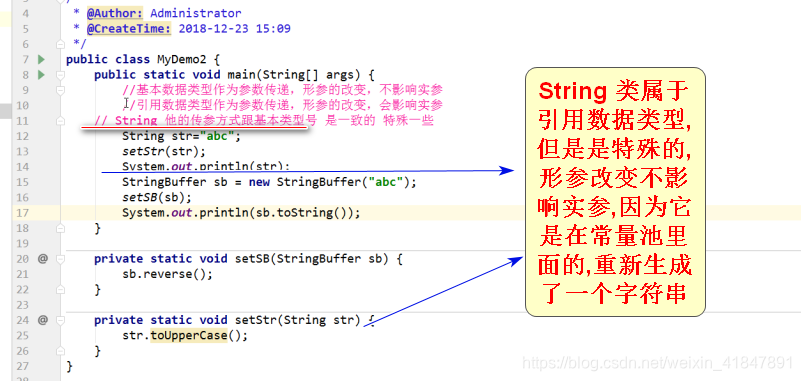
A:形式参数问题
String作为参数传递 String虽然是引用类型,但是它是一个常量,所以在做传递的时候,完全可以将其看成基本数据类型数据进行传递，形参改变不影响实参
StringBuffer作为参数传递，形参改变影响实参

10 String与StringBuffer相互转化

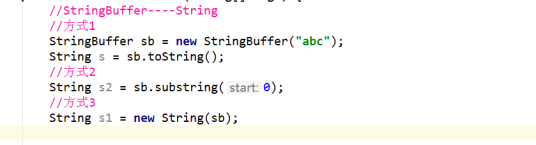
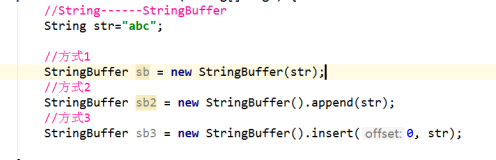
11 注意（算法排序问题）

3 冒泡排序

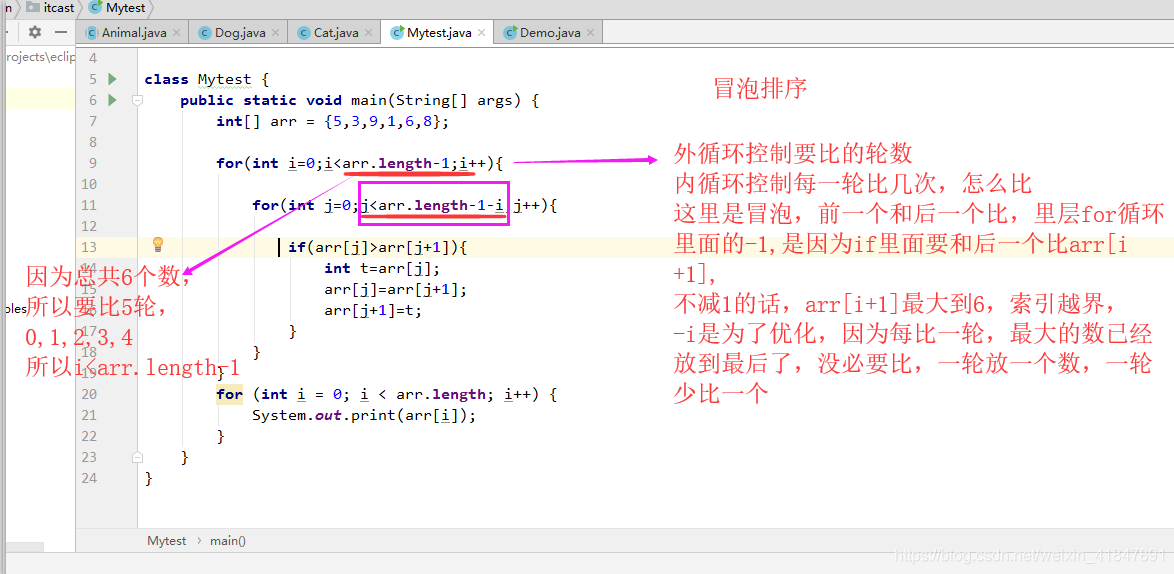
4 选择排序

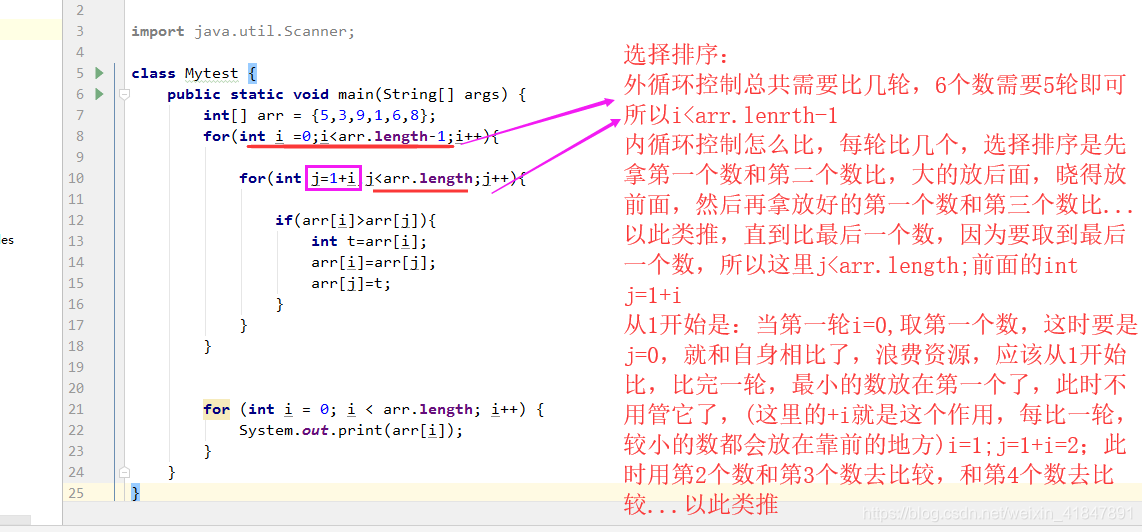
5 直接插入排序

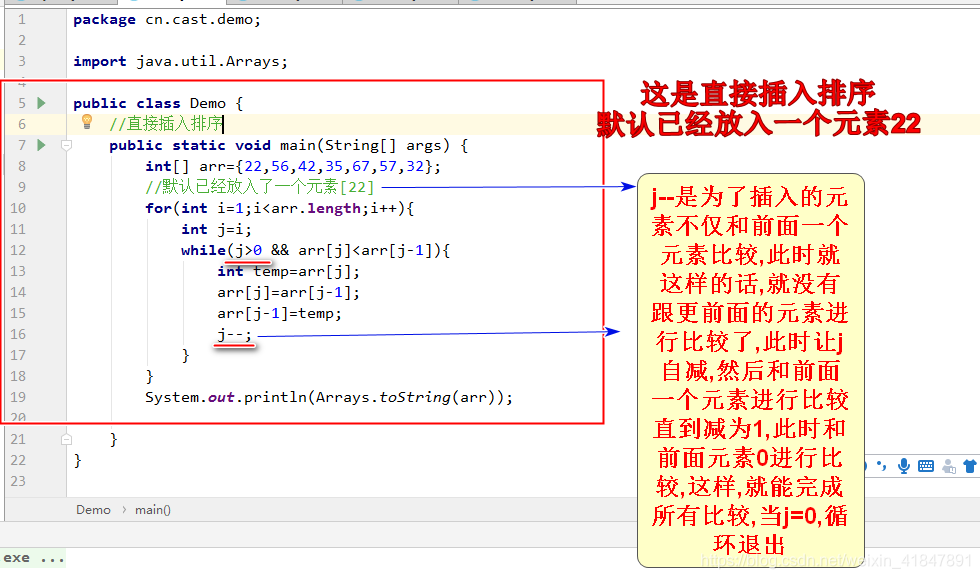
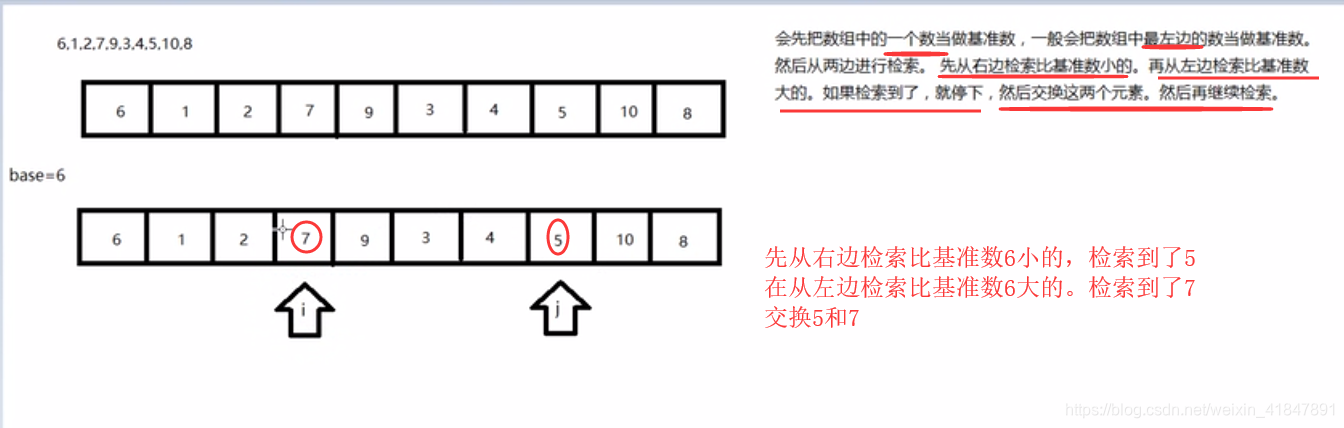
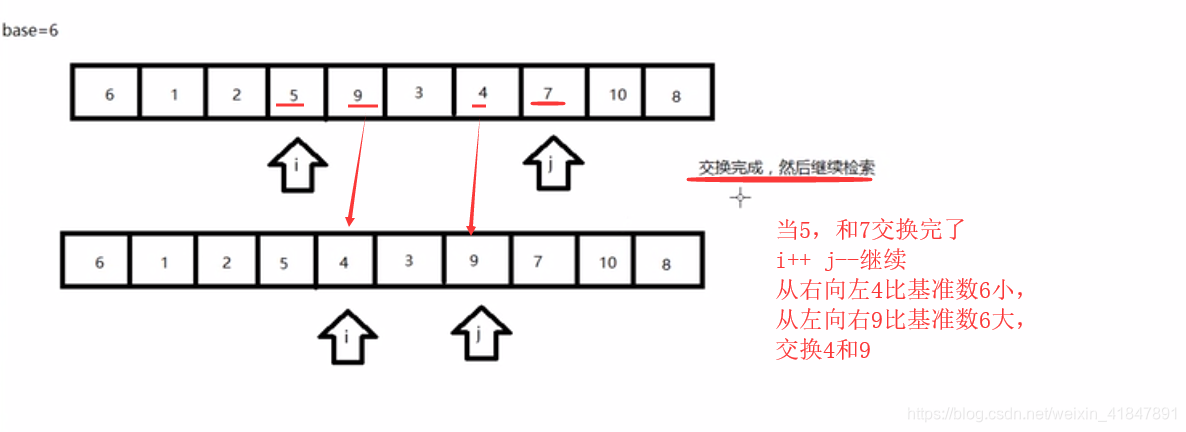
6 快速排序

方法一

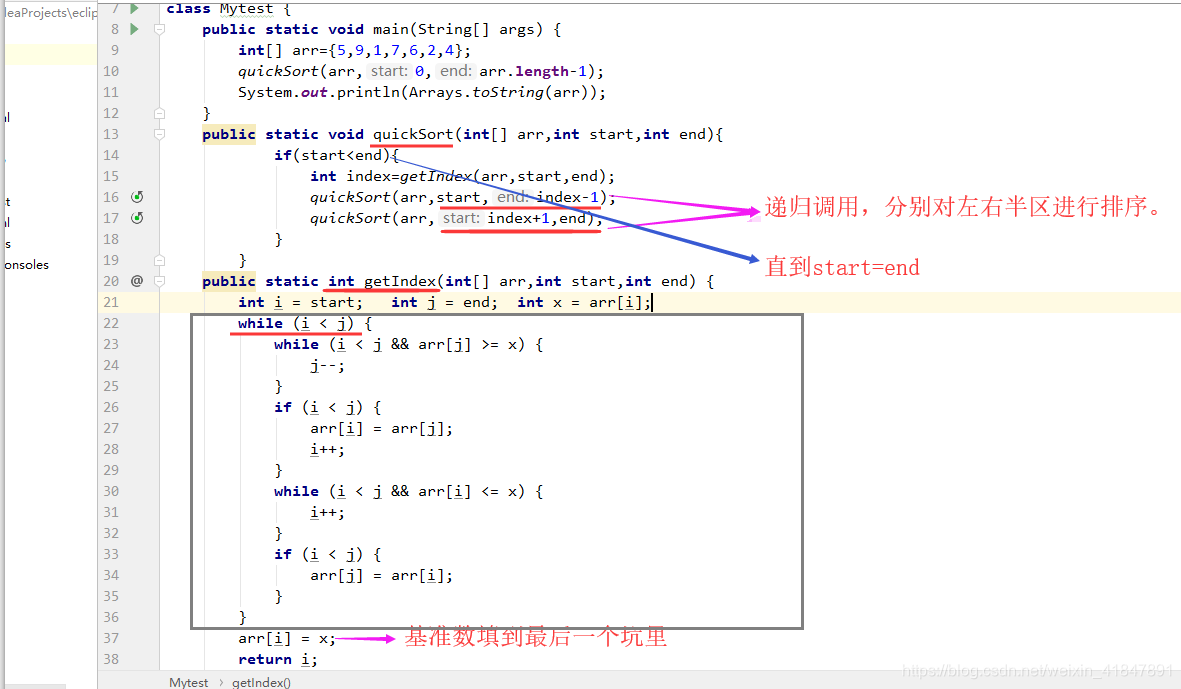
方法二

public class Main {
    public static void main(String[] args) {
        int[] arr={6,3,7,8,5,1,4,2};
        //调用方法，进行快速排序
        quickSork(arr,0,arr.length-1);

        //遍历数组
        for(int i=0;i<arr.length;i++){
            System.out.print(arr[i]);
        }


    }
   
     public static void quickSork(int[] arr,int left,int right){
        
        //进行判断，如果左边索引比右边索引更大，是不合法的，直接return结束这个方法
        if(left>right){
            return ;
        }
        
        //定义变量保存基准数
        int base=arr[left];
        
        //定义变量i，指向最左边
        int i=left;
       
        //定义变量j，指向最右边
        int j=right;
        
        //当i和j不相遇的时候，在循环中进行检索
        while(i !=j){
            
            //先由j从右往左检索比基准数小的，如果检索到比基准数小的时候就停下
            
            //如果检索的数比基准数大的或者相等的，就继续检索
            while(arr[j]>=base && i<j){
                j--;  //j从右往左移动
            }

           
            //i从左往右检索。
            while(arr[i]<=base && i<j){
                i++;//i从左往右移动
            }
            
            //代码走到这里。i停下了，j也停下了，然后交换i和j位置的元素。
            int temp=arr[i];
            arr[i]=arr[j];
            arr[j]=temp;
        }

        //如果上面的while循环的条件不成立。会跳出这个循环，往下执行
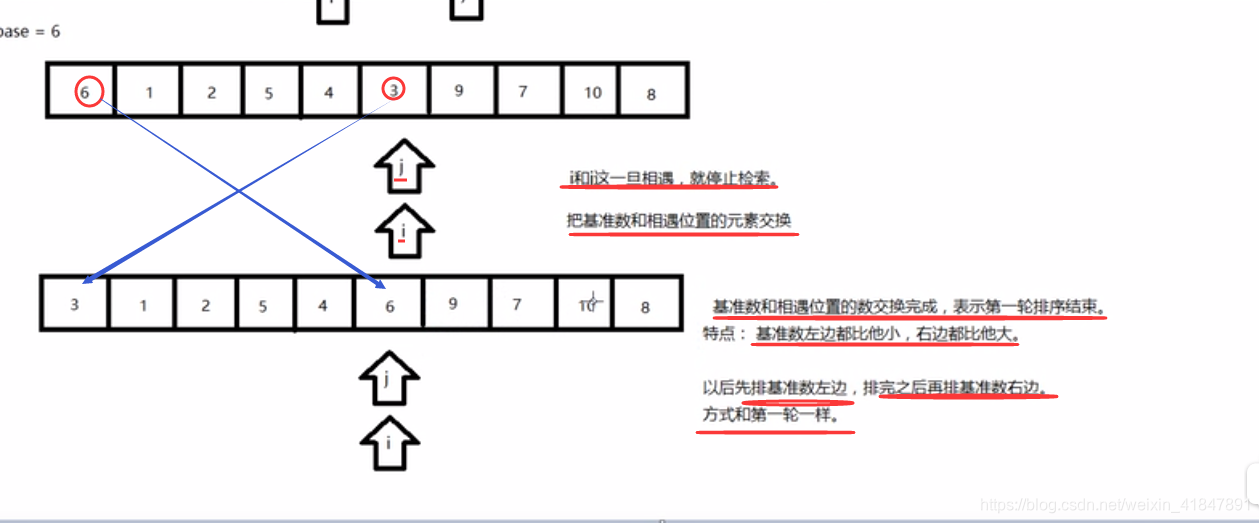
        //如果这个条件不成立说明i和j相遇了，即i=j.
        //如果i和j相遇了，就交换基准数这个元素和相遇位置的元素

        arr[left]=arr[i]; //把相遇位置的元素赋值给基准数这个位置的元素
        arr[i]=base;  //把基准数复制给相遇位置的元素。

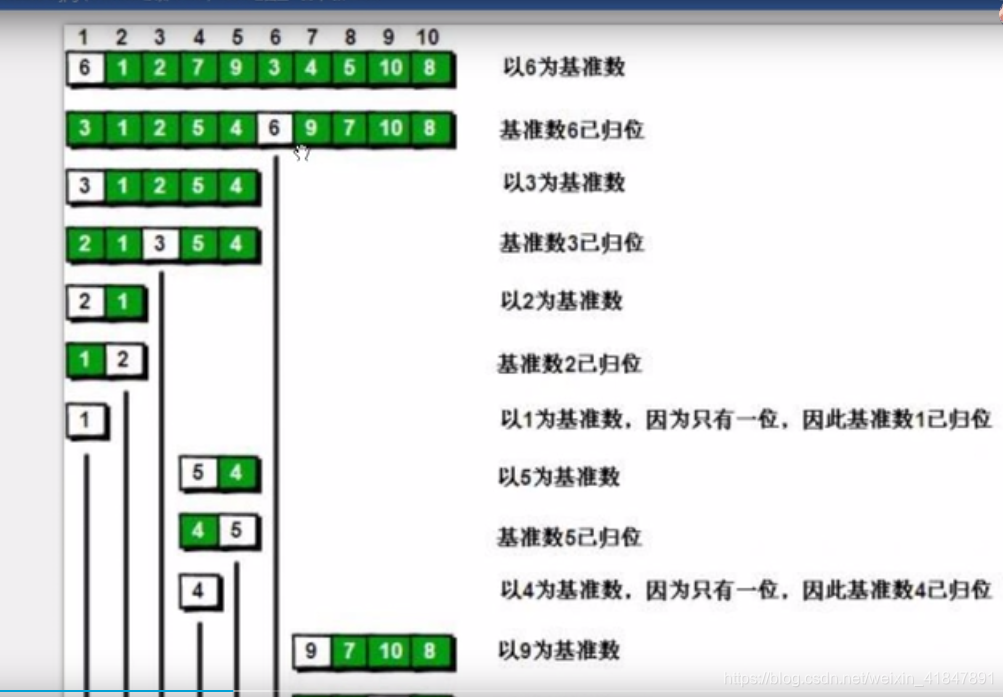
        //基准数在这里就归位了，左边的数字都比他小，右边的都比他大

        //接着，排基准数的左边
        quickSork(arr,left,i-1);

        //排右边
        quickSork(arr,j+1,right);   //这里i=j,随便用哪个都行
    }

7 归并排序（就是递归和分治的思想）

public class Main1 {
    public static void main(String[] args) {
        int[] arr={8,2,9,10,4,3,6,7};
        int L=0;
        int R=arr.length-1;
        //int M=(L+R)/2;
        mergeSort(arr,L,R);
        for(int i=0;i<arr.length;i++){
            System.out.println(arr[i]);
        }
    }
    
    
    public static void merge(int arr[],int L,int M,int R){
        int left_size=M-L+1;
        int right_size=R-M;

        int[] left=new int[left_size];  //定义左边小数组
        int[] right=new int[right_size];  //定义右边小数组
        for(int i=L;i<M+1;i++){         //从大数组里取左边部分填充左小数组
            left[i-L]=arr[i];

        }
        for(int i=M+1;i<=R;i++){      // 从大数组里取右边部分填充右小数组
            right[i-(M+1)]=arr[i];
        }
       int i=0,j=0,k=L;
        while (i<left_size && j<right_size){   //依次从0位置，将左小数组与右小数组进行比较
            if(left[i]<right[j]){        //如果左小数组里面数小，将其填充到大数组里面
                arr[k]=left[i];
                i++;
                k++;
            }else{
                arr[k]=right[j];       //否则将右小数组里面数，填充到大数组里面
                j++;
                k++;
            }
        }
        while(i<left_size){    //如果不满足上面的while循环条件，代表右小数组已经全部填到大数
                                //组里面去了.这时把左小数组里面剩下的数全填到大数组里面
            arr[k]=left[i];
            i++;
            k++;
        }
        while(j<right_size){   //如果不满足上面的while循环条件，代表左小数组已经全部填到大数
                                //组里面去了.这时把右小数组里面剩下的数全填到大数组里面
            arr[k]=right[j];
            j++;
            k++;
        }
    }
    
    
    public static void mergeSort(int[] arr,int L,int R){
        if(L<R){
            int M=(L+R)/2;
            mergeSort(arr,L,M);        //此方法为了将数组一半切开，一半切开，（分治思想）直    
                                         到左右两边为1个元素                                                                      
            mergeSort(arr,M+1,R);      
            merge(arr,L,M,R);
        }
    }
}

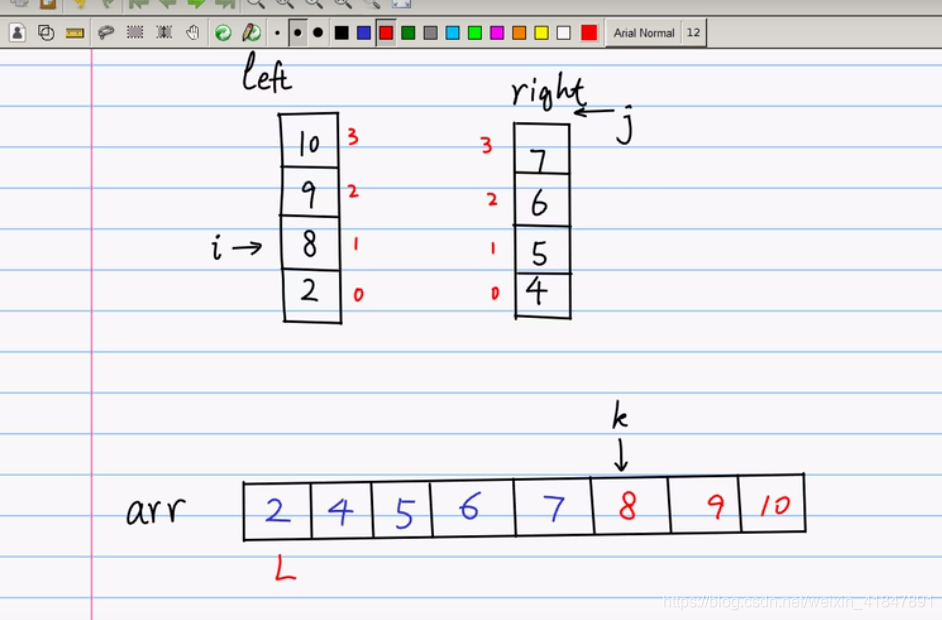
merge方法是为了将分好的两边的数组进行排序
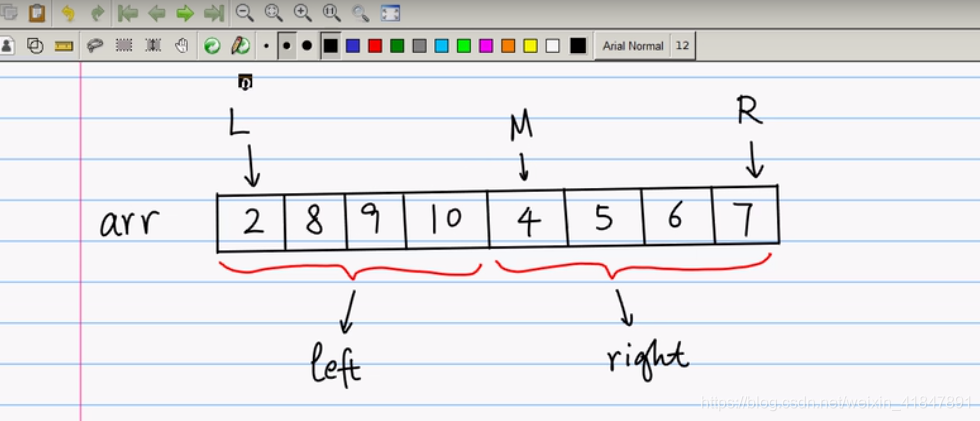
具体过程如下： M=(R-L)/2;  左边小数组left填充（L,M）个数据，右边小数组right填充（M+1,R）个数据
左边一个数组left, i指向左边的数组的0位置 i=0;
右边一个数组right，j指向右边的数组的0位置 j=0;
k=L=0;指向大数组arr;
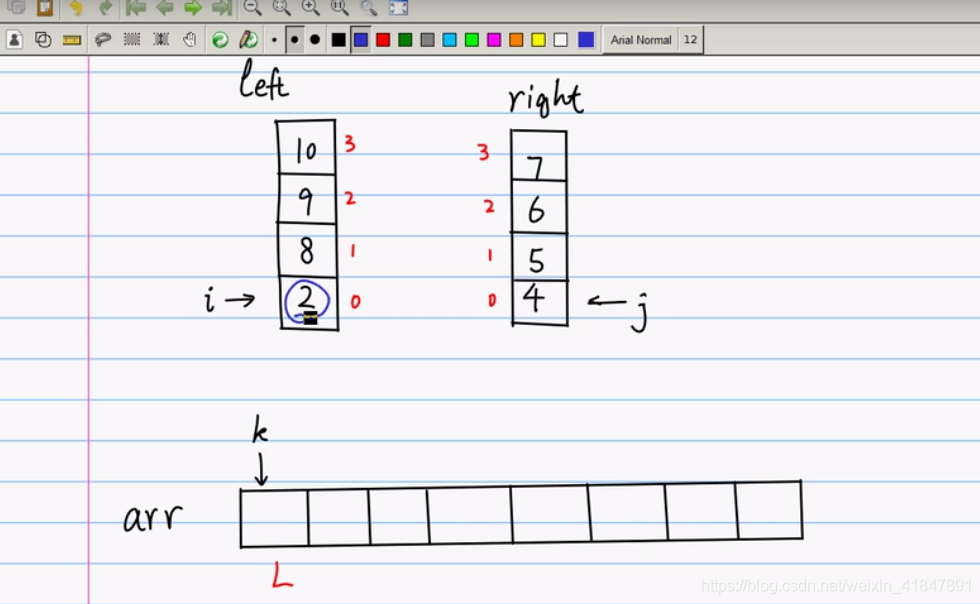
如果left[i]<right[j];就把小的这个数据放入大数组arr
arr[k]=left[i];
此时i,k都移动一格，i++;k++; 此时i=1;k=1;
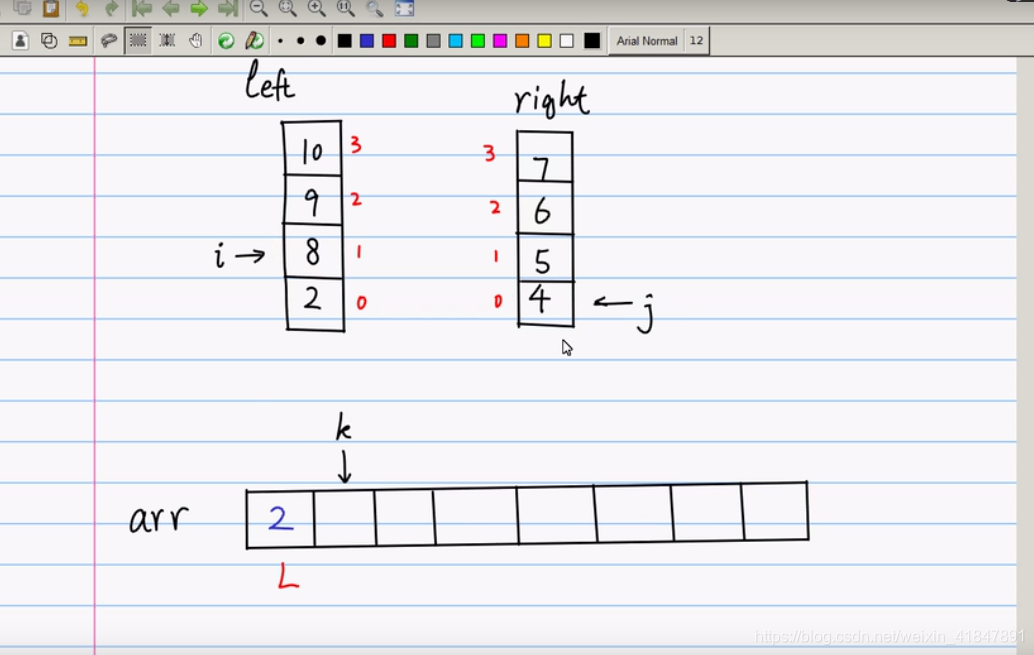
再让left[i]与right[j]比较；实际上此时是left[1]与right[0]比较；谁小谁放入；
若是right[0]小，就放入right[0]到arr[k]里面（arr[1]）；
此时j++;k++;
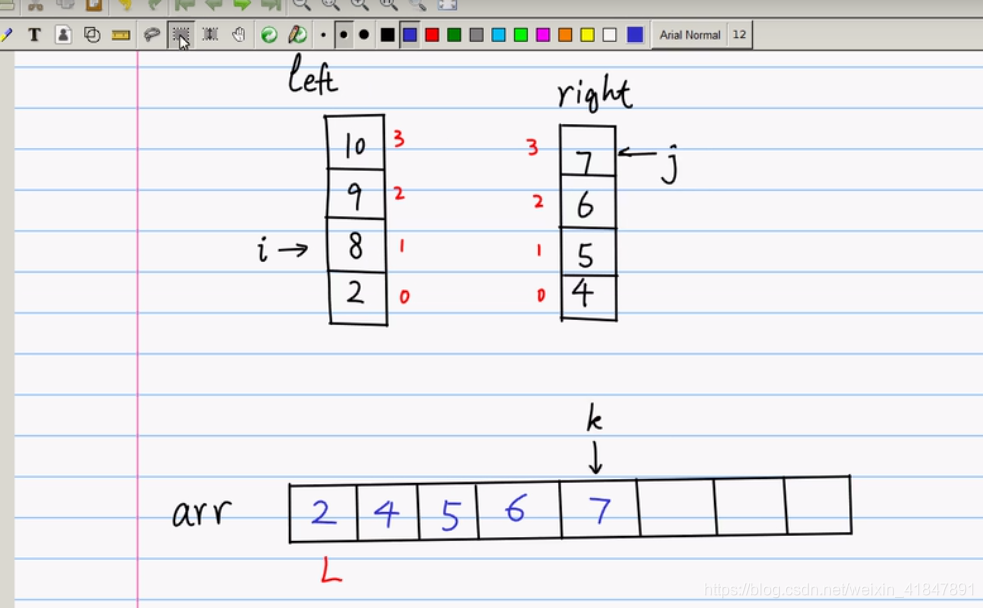
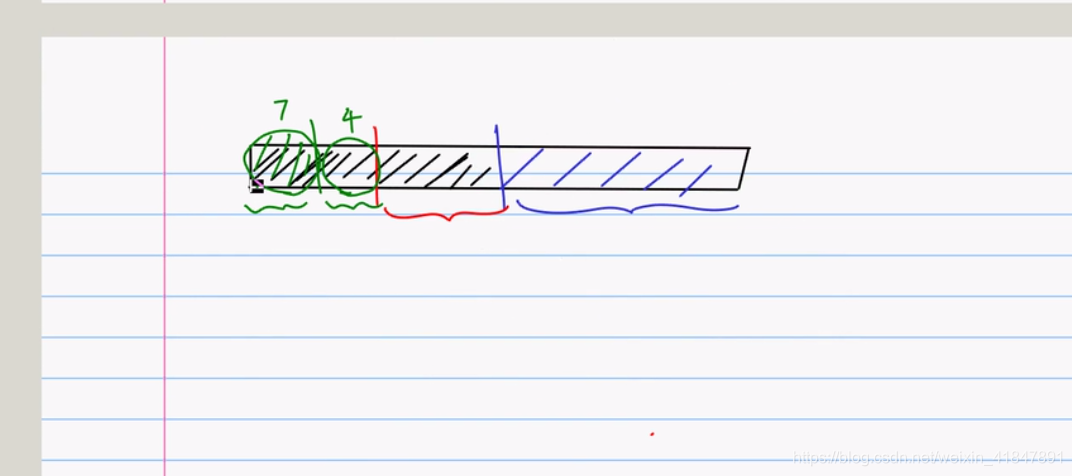
直到left数组与right数组有一个i，或者j跑到了该数组的最后一个元素了
就是说left，或者right有一个数组没有元素了，全比较完了；有一个数组里面的元素全填入到大数组arr了；

则把剩下的那个数组全填入大数组arr中


mergeSort方法是为了将数组不断分治，对半切，直到切成一个元素，即不符合L<R的条件，就不切了；然后递归调用merge方法

8 希尔排序（希尔排序就是插入排序的加强版，插入排序每次都是间隔为1进行比较，希尔排序间隔较大）

插入排序就是每次间隔为1进行排序
希尔排序每次都是以最大间隔进行排序，
这个最大间隔怎么计算呢
一般取 
      h=1
     while(h<arr.length/3){

            h=h*3+1
     }

那此题来说。arr.length=10；当h=1时，进入，1<10/3=3; h=3*1+1=4
然后因为4>3，不符合while循环的条件；此时h=4就是希尔排序的最大间隔；


然后以h=4为最大间隔进入后，一轮交换位置后，h=(h-1)/3=(4-1)/3=1;
然后以间隔为1进行排序，其实也就是插入排序

import java.util.*;
public class Main {
    public static void main(String[] args) {
        int[] arr={37,11,45,8,4,2,9,6,67,21};
        shellSort(arr);
        System.out.println(Arrays.toString(arr));

    }
    public static void shellSort(int[] arr){

        int h=1;
        while(h<arr.length/3){    //找一个最大的间隔
            h=h*3+1;
        }
        while(h>0){         // h要大于0

            for(int i=h;i<arr.length;i++){    //这边和直接插入排序一样，只是这里的间隔为h
               int j=i;
               while(j>h-1 && arr[j]<arr[j-h]){  //之前直接插入排序间隔为1，默认已经插入一
                                               //个元素（arr[0]），所以j>0,j从1开始与0位
                                               //置的元素比较，而这里间隔是h，假设h为4，第
                                              // 一个元素还是在0位置，下一个间隔比较的元素
                                              //就是0—>1—>2—>3—>4,所以看出就是4位置的元
                                              //素，所以要从4位置开始比，
                                              //j>h-1=3,j大于3,所以j从4开始
                  int temp=arr[j];
                  arr[j]=arr[j-h];
                  arr[j-h]=temp;
                  j-=h;
               }
            }
            h=(h-1)/3;        //最大间隔4比完，根据h=(h-1)/3求得下一个间隔，进行比较。直到
                              // h>0截止
        }
    }
}

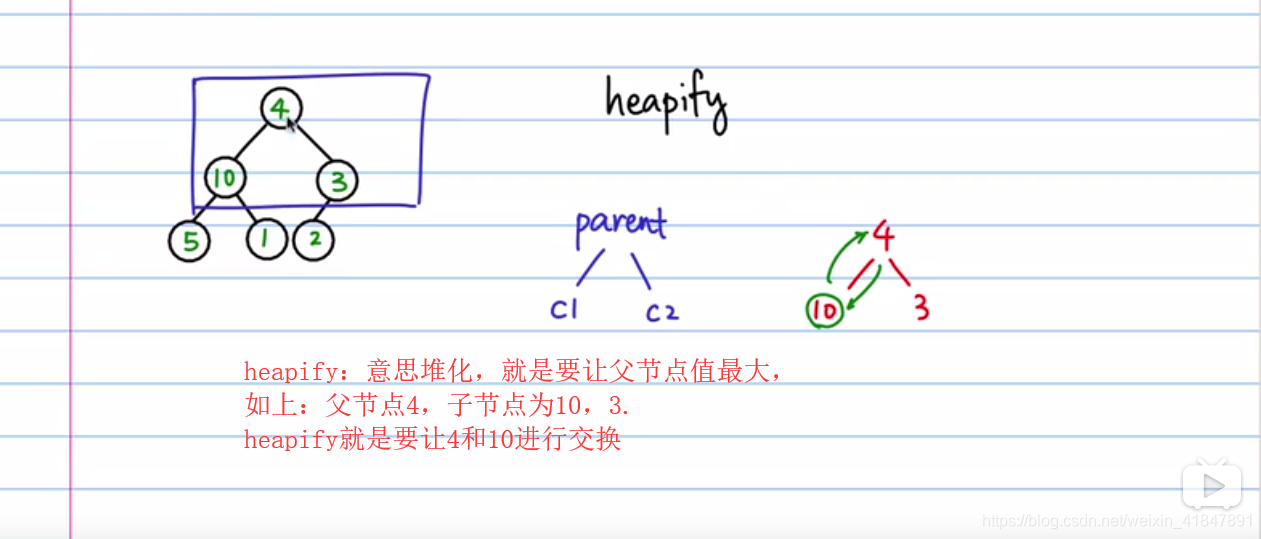
9 堆排序

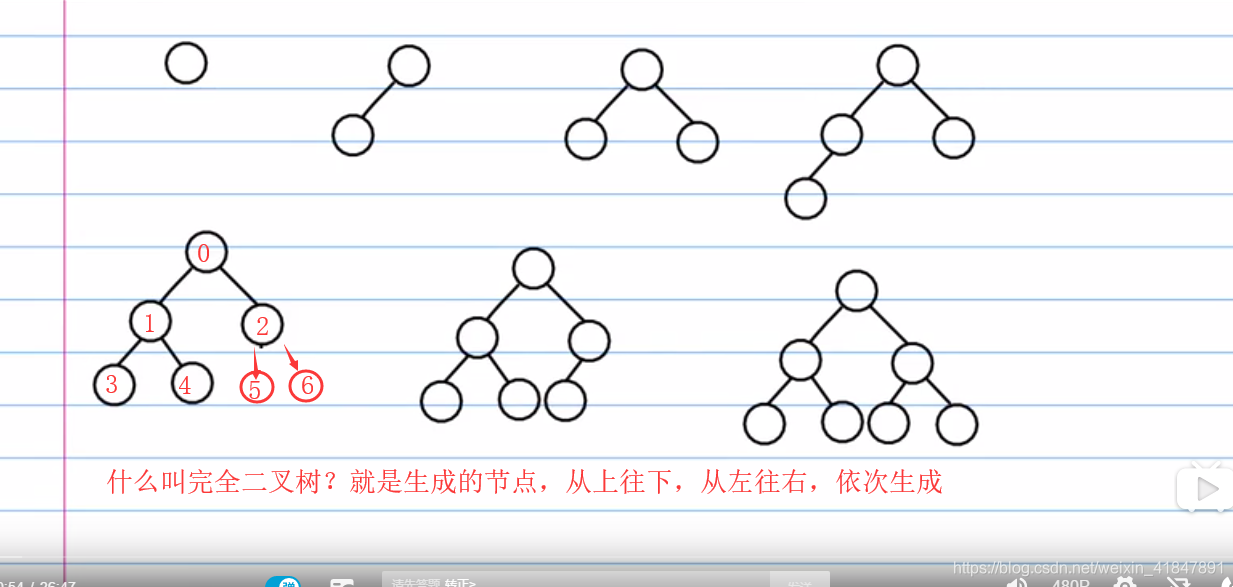
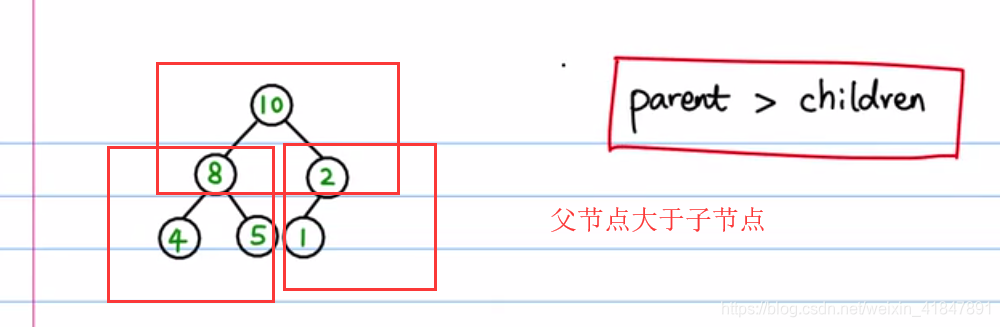
import java.util.Arrays;

public class Main3 {
    public static void main(String[] args) {
        int[] tree={19,2,11,1,10,18};
        int n=tree.length;
        heap_sort(tree,n);
        System.out.println(Arrays.toString(tree));
    }

    public static void heapify(int tree[], int n,int i ){
        if(i>=n){      //n为数组tree的长度，i为0-N ，为某一个节点
            return;
        }
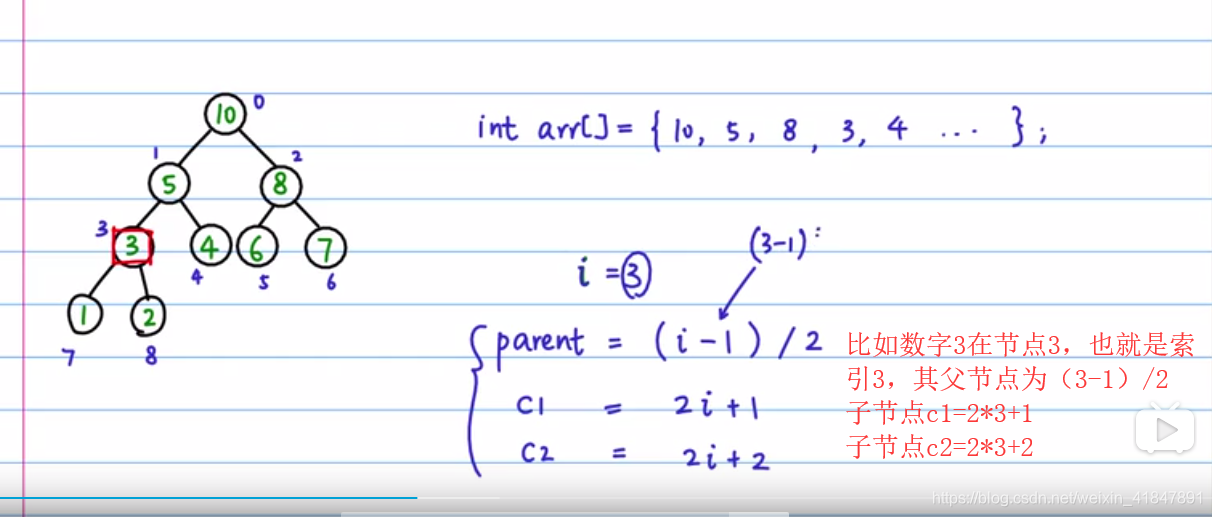
        int c1=2*i+1;   //若输入的是i节点，其两个子节点为2*i+1,2*i+2
        int c2=2*i+2;
        int max=i;       //max等于i节点
        if(c1<n && tree[c1]>tree[max]){
            max=c1;
        }
        if(c2<n && tree[c2]>tree[max]){
            max=c2;
        }
        if(max !=i){
            swap(tree,max,i);  //如果max不等于i,证明该父节点小于两个子节点中一个，需要交换该父节点与子节点的值
            heapify(tree,n,max);  //我觉得这一步可以省略，视频上有这一步
        }
    }
    public static void swap(int arr[],int i,int j){  //通过索引交换值
        int temp=arr[i];
        arr[i]=arr[j];
        arr[j]=temp;
    }
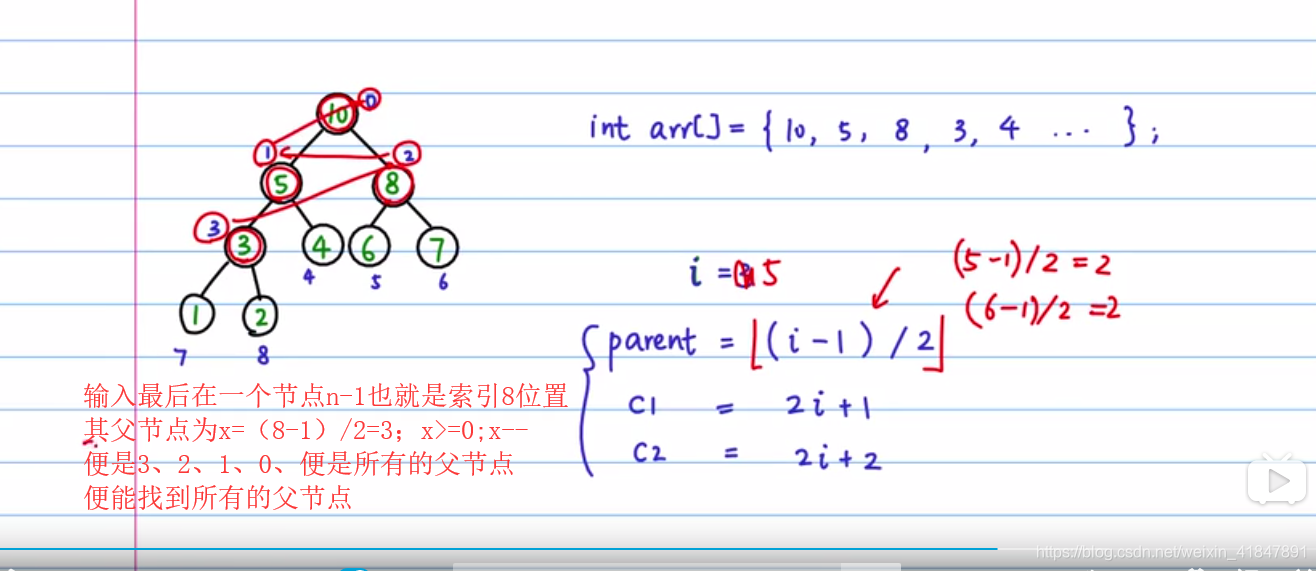
    public static void build_heap(int[] tree,int n){  //该方法作用是让头结点值最大，也就是总根节点值最大
        int last_node=n-1;                    //数组长度是n,最后一个索引是n-1
        int parent =(last_node-1)/2;         //该最后一个节点与其父节点是(i-1)/2的关系
        for(int i=parent;i>=0;i--){         //让i从最后一个节点的父节点开始递减遍历，遍历
            heapify(tree,n,i);               //的都是父节点，直到根节点，这样就保证了根节点的值最大
        }
    }
    public static void heap_sort(int tree[],int n){ //此方法作用是堆排序
        build_heap(tree,n);    //此方法作用是让头结点值最大，找到最大值
        for(int i=n-1;i>=0;i--){
            swap(tree,i,0);    //交换头结点的值与最后一个节点的值，即0与n-1的位置上的值，这
                      //样最后一个节点的值就在头结点位置上，头结点上最大的值在最后一个节点上。
            heapify(tree,i,0);  //这里的堆化从i开始（一开始i=n-1,也就是最后一个节点，
//i--后，i=n-1-1;现在是倒数第二个节点了。为什么堆化从倒数第二个节点开始呢？因为上一步已经把最大
//的值放在了最后一个节点了，已经排好序了，不需要管他了，不需要管最后一个值了）
        }
    }
}