2.4 算法和数据操作

参考：

1. 所有offer题目的LeetCode链接及python实现
2. github Target offer

摘要

很多算法都可以用递归和循环两种不同的方式实现。

• 通常基于递归的实现方法代码会比较简洁，但性能不如基于循环的实现方法。
• 位运算是把数字表示成二进制之后对0和1的操作。
  • 总共只有与、或、异或、左移和右移5种位运算。

2.4.1　查找和排序

查找：
顺序查找、二分查找、哈希表查找和二叉排序树查找
面试小提示：
如果面试题是要求在排序的数组（或者部分排序的数组）中查找一个数字或者统计某个数字出现的次数，我们都可以尝试用二分查找算法。

哈希表：

• 最主要的优点是我们利用它能够在O（1）时间查找某一元素，是效率最高的查找方式。
• 缺点是需要额外的空间来实现哈希表。

与二叉排序树查找算法对应的数据结构是二叉搜索树。
从额外空间消耗、平均时间复杂度和最差时间复杂度等方面去比较插入排序、冒泡排序、归并排序、快速排序等不同算法的优劣。

• 比如数组本身已经排好序了，而每一轮排序的时候都是以最后一个数字作为比较的标准，此时快速排序的效率只有 $O(n^2)$。因此在这种场合快速排序就不是最优的算法。
• 在面试的时候，如果面试官要求实现一个排序算法，那么应聘者一定要问清楚这个排序应用的环境是什么、有哪些约束条件，有多少辅助空间，在得到足够多的信息之后再选择最合适的排序算法。

面试题8：旋转数组的最小数字

牛客网链接
题目：
把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。

思路分析

解法一： 遍历查找 $O(n)$
从头到尾遍历数组一次，找出最小的元素及其对应的索引，最后形成输出结果。
解法二： 二分查找 $O(logn)$

• 定义三个指针：分别指向数组开头 start、结尾 end、中间位置 mid；
• if A[start] <= A[mid]: 即 mid 位于前面的递增子数组，数组中最小的元素应该位于该中间元素的后面，更新 start = mid；
• else: 即 mid 位于后面的递增子数组，数组中最小的元素应该位于该中间元素的前面，更新 end = mid；
• 以上两步骤之后，查找范围都会缩小到原来的一半；
• 最终 start 指针将指向前面子数组的最后一个元素，end指针会指向后面子数组的第一个元素。也就是它们最终会指向两个相邻的元素，而 end 指针指向的刚好是最小的元素。这就是循环结束的条件。 end - start == 1，min = A[end]

题目中的特例1：
数组本身就是有序的，无需旋转。
为支持这种情况，把indexMid初始化为indexStart；若发现第一个数字小于最后一个数字，则可以直接返回第一个数字。

程序1：

# -*- coding:utf-8 -*-
class Solution:
    def minNumberInRotateArray(self, rotateArray):
        if rotateArray == []:
            return 0
        _len = len(rotateArray)
        left = 0
        right = _len - 1
        while left <= right:
            mid = int((left + right) >> 1)
            if rotateArray[mid]<rotateArray[mid-1]:
                return rotateArray[mid]
            if rotateArray[mid] >= rotateArray[right]:
                # 说明在【mid，right】之间
                left = mid + 1
            else:
                # 说明在【left，mid】之间
                right = mid - 1
        return rotateArray[mid]

程序2：

# -*- coding:utf-8 -*-
class Solution:
    def minNumberInRotateArray(self, rotateArray):
        # write code here
        if not rotateArray:
            return 0
        start = mid = 0
        end = len(rotateArray)-1
        while rotateArray[end] <= rotateArray[start]:
            if end - start == 1:
                mid = end
                break
            # 二进制写法：
            # mid = int((left + right) >> 1)
            mid = (start+end)//2
            if rotateArray[start] <= rotateArray[mid]:
                start = mid
            elif rotateArray[end] >= rotateArray[mid]:
                end = mid
        return rotateArray[mid]

题目中的特例2：
当三个指针所指的元素都相同时，无法更新指针，

这种情况需要采用顺序查找的方法。
程序修改：

1. 添加一个子方法，实现顺序查找；
2. 在原函数中添加判断（是否三个指针所指数字相同），若相同，则跳转到顺序查找子函数。

2.4.2 递归和循环

递归是在一个函数的内部调用这个函数自身。
优点：代码简洁
缺点：有时间和空间的消耗

1. 每一次函数调用，都需要在内存栈中分配空间以保存参数、返回地址及临时变量，而且往栈里压入数据和弹出数据都需要时间。
2. 可能会导致栈溢出，每个进程的栈的容量是有限的，当递归调用的层级太多时，就会超出栈的容量，从而导致调用栈溢出。
3. 存在重复的计算

循环则是通过设置计算的初始值及终止条件，在一个范围内重复运算。

面试题9：斐波那契数列

题目一：写一个函数，输入n，求斐波那契（Fibonacci）数列的第n项。斐波那契数列的定义如下：

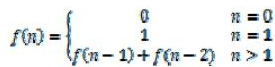
思路解析

递归

如果使用递归，会出现重复计算太多 + 随着n增大使层级过多的情况，有很严重的效率问题；时间复杂度是以n的指数的方式递增的。

循环

时间复杂度是 $O(n)$
改进：保存 f(n-1) 和 f(n-2) 结果，避免重复计算过多的情况。

minusOne, minusTwo = 1, 0
for i in range(n+1):
	ans = minusOne + minusTwo
	minusOne, minusTwo = ans, minusOne
return ans

题目二：青蛙跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

思路解析

n=1：只有一种跳法；
n=2：有 $f(1{)}^2+2/2$ 种跳法；
n>2：第一次跳的时候就有两种不同的选择

1. 第一次只跳1级，此时跳法数目等于后面剩下的n－1级台阶的跳法数目，即为f（n－1）；
2. 第一次跳2级，此时跳法数目等于后面剩下的n－2级台阶的跳法数目，即为f（n－2）。
3. 因此n级台阶的不同跳法的总数 $f(n)=f(n-1)+f(n-2)$。不难看出,这实际上就是斐波那契数列了。

本题扩展1：

在青蛙跳台阶的问题中，如果把条件改成：一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级，此时该青蛙跳上一个n级的台阶总共有多少种跳法？
思考：在 $dp[n]=dp[n-1]+dp[n-2]+..+dp[1]+1$(直接跳n)步骤 ,
即 $dp[n]={\sum }_{i=1}^{n-1}dp[i]+1=2\ast dp[n-1]=2^{n-1}$种跳法

class Solution:
    def jumpFloorII(self, number):
        # write code here
        if number == 1 or number == 2:
            return number
        ret = 1+1+2
        for i in range(number-2):
            ret = 2 * ret
        return ret 

相关题目2：

我们可以用2×1（图2.13的左边）的小矩形横着或者竖着去覆盖更大的矩形。请问用8个2×1的小矩形无重叠地覆盖一个2×8的大矩形（图2.13的右边），总共有多少种方法？

图中所示的覆盖方法记作 $f(8)$.
用左边1*2覆盖大矩形最左边时候，有两个选择：横着放或者竖着放；

• 横着放：还剩下2*6的矩形区域，即 $f(6)$.
• 竖着放：还剩下2*7的矩形区域，即 $f(7)$.
• 综上， $f(8)=f(7)+f(6)$. 即斐波那契数列。