树与二叉树的奇妙世界-优快云博客

树

在这里插入图片描述
1.树的基本概念
树是n(n≥0)个结点的有限集合T。当n=0时，称为空树；当n>0时，该集合满足如下条件：
（1）其中必有一个称为根的特定结点，它没有直接前驱，但有零个或多个直接后继。
（2）其余n-1个结点可以划分成m(m≥0)个互不相交的有限集T₁,T₂,…T_m,其中T_i又是一棵树，称为根的子树。每颗子树的根结点有且仅有一个直接前驱，但有零个或多个直接后继。
2.树的存储结构
（1）双亲表示法
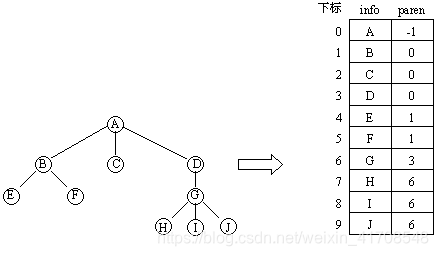
在这里插入图片描述
定义如下：

#define MAX 100
typedef struct TNode
{
	DataType data;
	int parent;
}TNode;
typedef struct
{
	TNode tree[MAX];
	int nodenum;
}ParentTree;

（2）孩子表示法
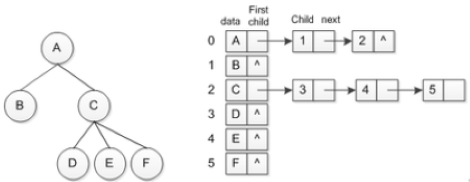
在这里插入图片描述
把每个结点的孩子结点排列起来，构成一个单链表，称为孩子链表。n个结点共有n个孩子链表（叶子结点的孩子链表为空表），而n个结点的数据和n个孩子链表的头指针又组成一个顺序表。
定义如下：

typedef struct ChildNode			/*孩子链表结点的结构定义*/
{
	int Child;						/*该孩子结点在线性表中的位置*/
	struct ChildNode *next;			/*指向下一个孩子结点的指针*/
}ChildNode;
typedef struct						/*顺序表结点的结构定义*/
{
	DataType data;					/*结点的信息*/
	ChildNode *FirstChild;			/*指向孩子链表的头指针*/
}DataNode;
typedef struct						/*树的定义*/
{
	DataNode nodes[MAX];			/*顺序表*/
	int root;						/*该树的根结点在线性表中的位置*/
	int num;						/*该树的结点个数*/
}ChildTree;

（3）孩子兄弟表示法
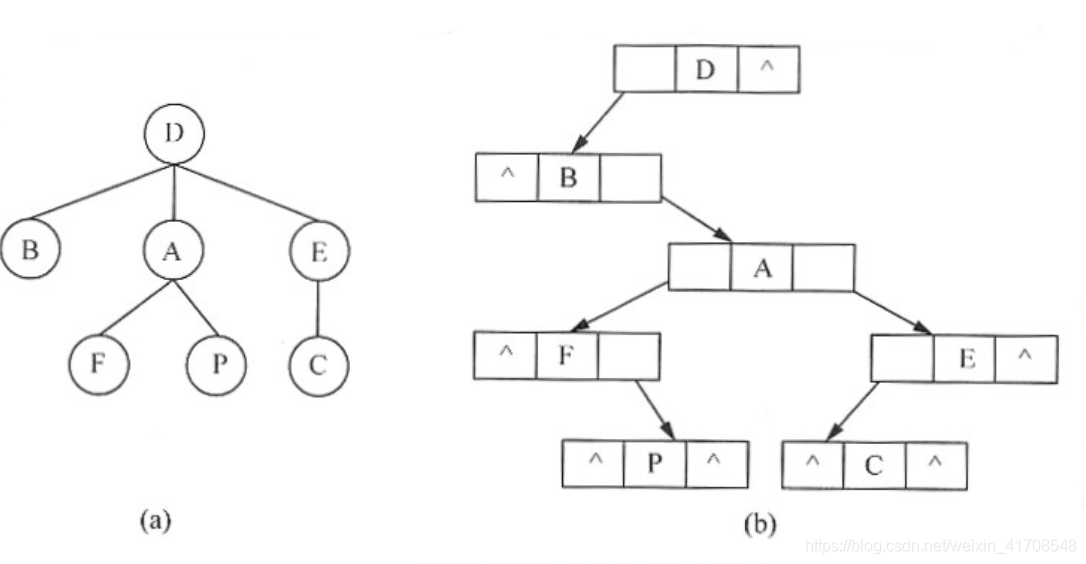
在这里插入图片描述
定义如下：

typedef struct CSNode
{
	DataType data;					/*结点信息*/
	Struct CSNode *FirstChild;		/*第一个孩子*/
	Struct CSNode *NextSibling;		/*下一个兄弟*/
}CSNode,*CSTree;

二叉树

在这里插入图片描述
1.二叉树的定义
把满足以下条件的树称为二叉树
（1）每个结点的度都不大于2
（2）每个结点的孩子结点次序不能任意颠倒
即一个二叉树中的每个结点只能含有0、1或2个孩子，而且每个孩子有左右之分，位于左边的孩子称为左孩子，位于右边的孩子称为右孩子。
补充两种特殊的二叉树：满二叉树和完全二叉树
满二叉树：深度为k且有2^k-1个结点的二叉树
完全二叉树：深度为k，结点数为n的二叉树，如果其结点1~n的位置序号分别与等高的满二叉树的结点 1~n的位置序号一一对应，则为完全二叉树
2.二叉树的性质：
（1）在二叉树的第i层上至多有2^i-1个结点（i≥1）。
（2）深度为k的二叉树至多有2^k-1个结点（k≥1）。
（3）对任意一颗二叉树T，若终端结点数为n0，度数为2的结点数为n2，则n0=n2+1。
（4）具有n个结点的完全二叉树的深度为[log₂n]+1
3.二叉树的存储结构
（1）顺序存储结构
对于完全二叉树来说，用一维数组作存储结构，将二叉树中编号为i的结点存放在数组的第i个分量中。这样既不浪费空间，又可以根据公式计算出每一个结点的左、右孩子的位置。
但是对于一般的二叉树来说：必须用虚结点将其补成一颗完全二叉树来存储，这就会造成空间浪费。
（2）链式存储结构
对于任意的二叉树来说，每个结点只有一个双亲结点（根除外），最多有两个孩子。可以设计每个结点至少包括三个域：数据域、左孩子域和右孩子域。
二叉链表结点结构：

typedef struct Node
{
	DataType data;
	struct Node*LChild;
	struct Node*RChild;
}BiTNode,*BiTree;

4.二叉树的遍历
二叉树是非线性数据结构，通过遍历可以将二叉树中的结点访问一次且仅一次，从而得到访问结点的顺序序列。遍历操作目的在于将非线性化结构变成线性化的访问序列。
三种遍历算法：
（1）先序遍历二叉树

void PreOrder(BiTree root)
{
	if(root!=NULL)
	{
		Visit(root->data);			/*访问根节点*/
		PreOrder(root->LChild); 	/*遍历左子树*/
		PreOrder(root->RChild); 	/*遍历右子树*/
	}
}

（2）中序遍历二叉树

void InOrder(BiTree root)
{
	if(root!=NULL)
	{
		InOrder(root->LChild);
		Visit(root->data);
		InOrder(root->RChild);
	}
}

（3）后序遍历二叉树

void PostOrder(BiTree root)
{
	if(root!=NULL)
	{
		PostOrder(root->LChild);
		PostOrder(root->RChild);
		Visit(root->data);
	}
}

遍历算法应用：
（1）输出二叉树中的结点
输出二叉树中的结点无次序要求，可用三种遍历算法中的任何一种完成。

void PreOrder(BiTree root)
{
	if(root!=NULL)
	{
		printf(root->data);
		PreOrder(root->LChild);
		PreOrder(root->RChild);
	}	
}

（2）输出二叉树中的叶子结点

void PreOrder(BiTree root)
{
	if(root!=NULL)
	{
		if(root->LChild==NULL && root->RChild==NULL)
			printf(root->data);
		PreOrder(root->LChild);
		PreOrder(root->RChild);
	}
}

（3）统计叶子结点数目
同样无次序要求，可用三种遍历算法中任何一种完成。
方法一：后序遍历实现

void leaf(BiTree root)
{
	if(root!=NULL)
	{
		leaf(root->LChild);
		leaf(root->RChild);
		if(root->LChild==NULL && root->RChild==NULL)
			LeafCount++;
	}
}

方法二：采用分治算法
如果是空树，返回0；如果只有一个结点，返回1；否则为左右子树的叶子结点数之和。

int leaf(BiTree root)
{
	int LeafCount;
	if(root==NULL)
		LeafCount=0;
	else if((root->LChild==NULL)&&(root->RChild==NULL))
		LeafCount=1;
	else
		LeafCount=leaf(root->LChild)+leaf(root->RChild);
	return LeafCount;
}

（4）创建二叉链表（使用扩展先序遍历序列）
给定一颗二叉树，可以得到它的遍历序列；反过来，给定一颗二叉树的遍历序列，也就可以创建相应的二叉链表。

void CreateBiTree(BiTree *bt)
{
	char ch;
	ch=getchar();
	if(ch=='.')
		*bt=NULL;
	else
	{
		*bt=(BiTree)malloc(sizeof(BiTNode));
		(*bt)->data=ch;
		CreateBiTree(&((*bt)->LChild));
		CreateBiTree(&((*bt)->RChild));
	}
}

（5）求二叉树的高度
二叉树的高度（深度）为二叉树中结点层次的最大值，也可视为其左、右子树高度的最大值加一。
方法一：

int PostTreeDepth(BiTree bt)
{
	int hl,hr,max;
	if(bt!=NULL)
	{
		hl=PostTreeDepth(bt->LChild);
		hr=PostTreeDepth(bt->RChild);
		max=hl>hr?hl:hr;			/*求出左右子树深度较大者*/
		return(max+1);
	}
	else
		return 0;					/*空树则返回0*/
}

方法二：
depth为最大层次，h为结点所在层次

void PreTreeDepth(BiTree bt,int h)
{
	if(bt!=NULL)
	{
		if(h>depth)
			depth=h;
		PreTreeDepth(bt->LChild,h+1);
		PreTreeDepth(bt->RChild,h+1); 
	}
}

（6）按树状打印二叉树
要先打印右子树，再打印根，再打印左子树

void PrintTree(BiTree bt,int nLayer)
{
	if(bt==NULL)
		return;
	PrintTree(bt->RChild,nLayer+1);
	for(int i=0;i<nLayer;i++)
		printf(" ");
	printf("%c\n",bt->data);
	PrintTree(bt->LChild,nLayer+1);
}

5.二叉树的线索化
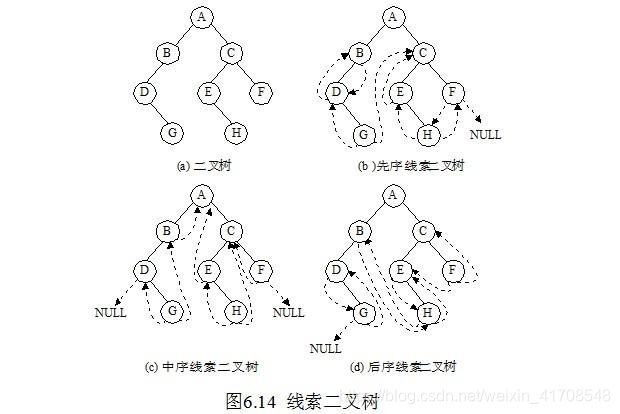
在这里插入图片描述
线索二叉树的概念：
二叉树的遍历运算只能找到结点的左、右孩子信息，不能直接得到结点在遍历序列中的前驱和后继信息。要得到这些信息可以充分利用二叉链表中的空链域，将遍历过程中结点的前驱、后继信息保存下来。为了区分孩子结点和前驱、后继结点，可以增设两个标志域，如下图所示：
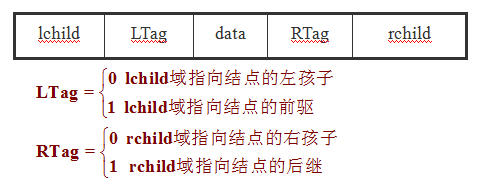
在这里插入图片描述
在这种存储结构中，指向前驱和后继结点的指针称为线索。以这种结构组成的二叉链表作为二叉树的存储结构，称为线索链表。对二叉树以某种次序进行遍历并且加上线索的过程称为线索化。线索化了的二叉树称为线索二叉树。
线索二叉树的算法：
（1）建立中序线索树
线索化的过程即为在遍历过程中修改空指针域的过程。对二叉树按照不同的遍历次序进行线索化，可以得到不同的线索二叉树，包括先序线索二叉树、中序线索二叉树和后序线索二叉树。这里介绍中序线索二叉树。

void Inthread(BiTree root)
{
	if(root!=NULL)
	{
		Inthread(root->LChild);			/*线索化左子树*/
		if(root->LChild==NULL)
		{
			root->Ltag=1;				/*置前驱线索*/
			root->LChild=pre;
		}
		if(pre!=NULL&&pre->RChild==NULL)
		{
			pre->Rtag=1;				/*置后继线索*/
			pre->RChild=root;
		]
		pre=root;						/*当前访问结点为下一个访问结点的前驱*/
		Inthread(root->RChild);			/*线索化右子树*/
	}
}

线索化左子树和线索化右子树之间为加线索操作。

（2）在线索二叉树中找前驱、后继结点
在中序线索树中找结点前驱：

BiTNode *InPre(BiTNode *p)
{
	if(p->tag==1)						/*直接利用线索*/
		pre=p->LChild;		
	else								/*在p的左子树中查找最右下端结点*/
	{						
		for(q=p->LChild;q->Rtag==0;q=q->RChild)
		pre=q;
	}
	return(pre);
}

在中序线索树中找结点后继：

BiTNode *InNext(BiTNode *p)
{
	if(p->Rtag==1)						/*直接利用线索*/
		Next=p->RChild;
	else								/*在p的右子树中查找最左下端结点*/
	{
		for(q=p->RChild;q->Ltag==0;q=q->LChild)
		Next=q;
	}
	return(Next);
}

（3）遍历中序线索树
在中序线索树上求中序遍历的第一个结点：

BiTNode *InFirst(BiTree bt)
{
	BiTNode *p=bt;
	if(!p)
		return(NULL);
	while(p->Ltag==0)					/*找最左*/
		p=p->LChild;
	return p;
}

遍历中序线索二叉树：

void TInOrder(BiTree bt)
{
	BiTNode *p;
	p=InFirst(bt);
	while(p)
	{
		visit(p);
		p=InNext(p);
	}
}

树、森林与二叉树的转换

1.树转换为二叉树
第一步：树中所有相邻兄弟之间加一条连线。
第二步：对树中的每个结点，只保留其与第一个孩子结点之间的连线，删去其与其他孩子结点之间的连线。
第三步：以树的根结点为轴心，将整棵树顺时针旋转一定的角度，使之结构层次分明。
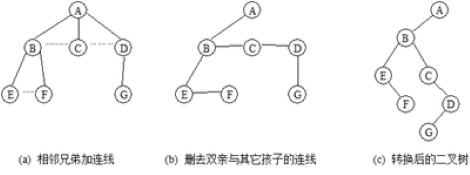
在这里插入图片描述
2.森林转换为二叉树
第一步：将森林中的每棵树转换成相应的二叉树
第二步：第一颗二叉树不动，从第二颗二叉树开始，依次把后一颗二叉树的根结点作为前一棵二叉树根结点的右孩子，当所有的二叉树连在一起后，所得到的二叉树就是由森林转换得到的二叉树。
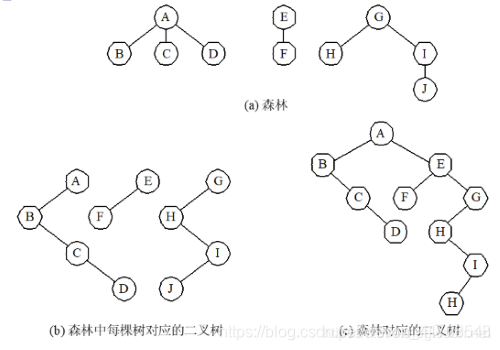
在这里插入图片描述
3.二叉树转换为树或森林
第一步：若某结点是其双亲的左孩子，则把该结点的右孩子、右孩子的右孩子…都与该结点的双亲结点用线连起来。
第二步：删掉原二叉树中所有双亲结点与右孩子结点的连线。
第三步：整理由第一步和第二步所得到的树或森林，使之结构层次分明。

哈夫曼树

1.哈夫曼树的概念
先来介绍几个基本概念：
路径： 从根结点到该结点的分支序列
路径长度： 从根结点到该结点所经过的分支数目
结点的权： 给树的结点赋予一个具有某种实际意义的实数
带权路径长度： 从树根到某一结点的路径长度与该结点的权的乘积
哈夫曼树： 由n个带权叶子结点构成的所有二叉树中带权路径长度最短的二叉树。哈夫曼树也称最优二叉树。
2.哈夫曼树的类型定义
用静态三叉链表来存储：
|权值 | 双亲序号 |左孩子序号|右孩子序号|
类型定义如下：
哈夫曼树没有度为1的结点，具有n个结点的哈夫曼树共有2n-1个结点。

#define N 20							/*叶子结点的最大值*/
#define M 2*N-1							/*所有结点的最大值*/
typedef struct
{
	int weight;							/*结点的权值*/
	int parent;							/*双亲的下标*/
	int LChild;							/*左孩子结点的下标*/
	int RChild;							/*右孩子结点的下标*/
}HTNode,HuffmanTree[M-1];				/*HuffmanTree是一个结构数组类型，0号单元不用*/

3.哈夫曼编码
哈夫曼编码定义：对一颗具有n个叶子结点的哈夫曼树，若对树中的每个左分支赋予0，右分支赋予1（也可左1右0），则从根到每个叶子的通路上，各分支的赋值分别构成一个二进制串，该二进制串就称为哈夫曼编码。
哈夫曼编码作用：哈夫曼编码是最优前缀码。利用哈夫曼编码，可以得到平均长度最短的编码，使各种报文对应的二进制串的平均长度最短。