Boosting（提升）算法之Adaboost

Boosting算法思想：

Boosting是一种框架算法,主要是通过对样本集的操作获得样本子集,然后用弱分类算法在样本子集上训练生成一系列的基分类器。他可以用来提高其他弱分类算法的识别率,也就是将其他的弱分类算法作为基分类算法放于Boosting 框架中,通过Boosting框架对训练样本集的操作,得到不同的训练样本子集,用该样本子集去训练生成基分类器;每得到一个样本集就用该基分类算法在该样本集上产生一个基分类器,这样在给定训练轮数 n 后,就可产生 n 个基分类器,然后Boosting框架算法将这 n个基分类器进行加权融合,产生一个最后的结果分类器,在这 n个基分类器中,每个单个的分类器的识别率不一定很高,但他们联合后的结果有很高的识别率,这样便提高了该弱分类算法的识别率。在产生单个的基分类器时可用相同的分类算法,也可用不同的分类算法,这些算法一般是不稳定的弱分类算法,如神经网络(BP) ,决策树(C4.5)等。如下图

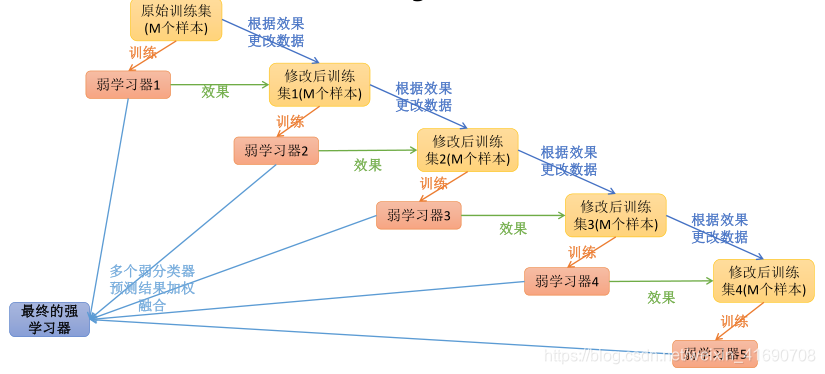
提升学习的常见算法模型为：Adaboost、GBDT、Xgboost

Adaboost算法分析

 算法原理：

Adaptive Boosting是一种迭代算法。每轮迭代中会在训练集上产生一个新的学习器，然后使用该学习器对所有样本进行预测，以评估每个样本的重要性(Informative)。换句话来讲就是，算法会为每个样本赋予一个权重，每次用训练好的学习器标注/预测各个样本，如果某个样本点被预测的越正确，则将其权重降低；否则提高样本的权重。权重越高的样本在下一个迭代训练中所占的比重就越大，也就是说越难区分的样本在训练过程中会变得越重要；整个迭代过程直到错误率足够小或者达到一定的迭代次数为止

   Adaboost的核心思想是通过反复修改数据的权重,从而使一系列弱学习器成为强可学习器.其核心步骤如下: 
- 权值调整,提升被错误分类的样本的权重,降低被正确分类的权重 
- 基分类器组合,采用加权多数表决算法,加大分类误差率较小的弱分类器的权重,减小误差大的.

可以构造出一个非常准确的强分类器。强分类器的计算公式为：

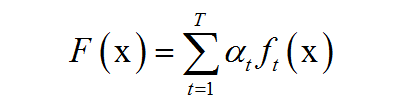
其中x是输入向量，F(x)是强分类器，ft(x)是弱分类器，αt是弱分类器的权重值，是一个正数，T为弱分类器的数量。弱分类器的输出值为+1或-1，分别对应于正样本和负样本。分类时的判定规则为：

其中sgn是符号函数。强分类器的输出值也为+1或-1，同样对应于正样本和负样本。弱分类器和它们的权重值通过训练算法得到。之所以叫弱分类器是因为它们的精度不用太高。

训练模型的过程：

训练时，依次训练每一个弱分类器，并得到它们的权重值。训练样本同样带有权重，初始时所有样本的权重相等，被前面的弱分类器错分的样本会加大权重，反之会减小权重，因此接下来的弱分类器会更加关注这些难分的样本。弱分类器的权重值根据它的准确率构造，精度越高的弱分类器权重越大。给定l个训练样本(xi,yi)，其中xi是特征向量，yi为类别标签，其值为+1或-1。训练算法的流程如下：

初始化样本权重值，所有样本的初始权重相等：

循环，对t=1,…,T依次训练每个弱分类器：

训练一个弱分类器ft(x)，并计算它对训练样本集的错误率et

计算弱分类器的权重：

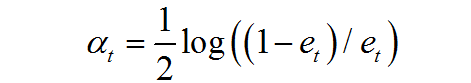
更新所有样本的权重：

其中Zt为归一化因子，它是所有样本的权重之和：

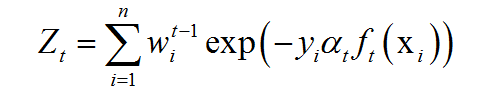
结束循环

最后得到强分类器：

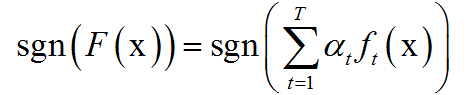
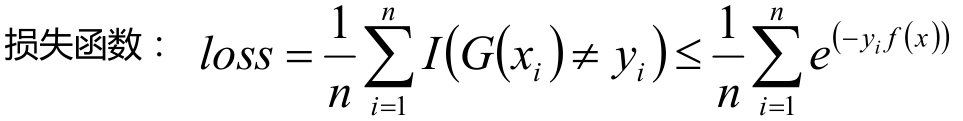
损失函数取

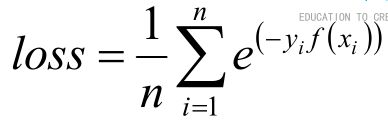
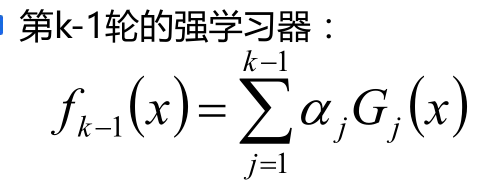
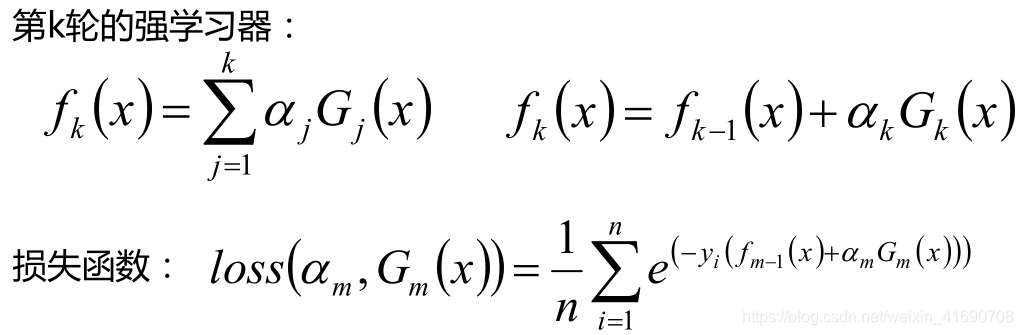
总而言之关注之前被错分的样本，准确率高的弱分类器有更大的权重。

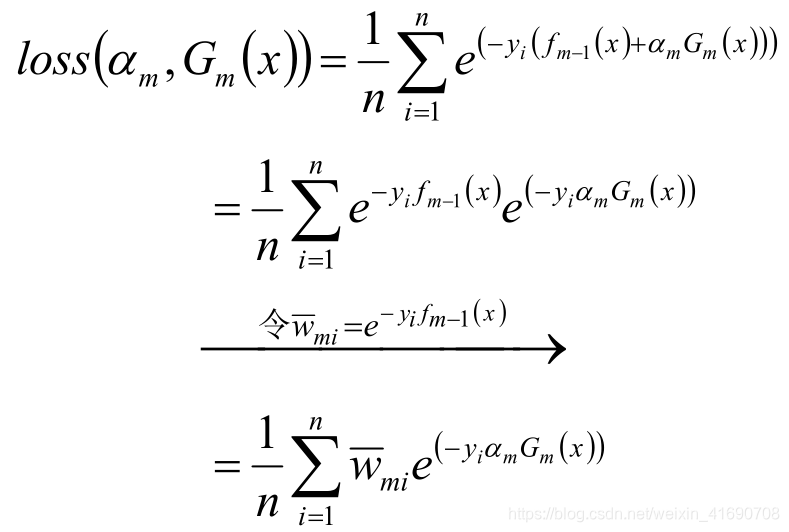
Adaboost算法构建过程：

过程1

过程2

优缺点：

本文主要参考西瓜书和统计学习（李航版本）