线性分类器
一、线性分类器:
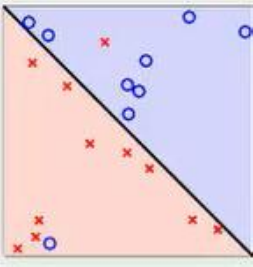
首先给出一个非常非常简单的分类问题(线性可分),我们要用一条直线,将下图中黑色的点和白色的点分开,很显然,图上的这条直线就是我们要求的直线之一(可以有无数条这样的直线)
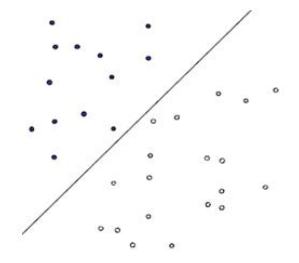

假如说,我们令黑色的点 = -1, 白色的点 = +1,直线f(x) = w.x + b当向量x的维度=2的时候,f(x) 表示二维空间中的一条直线, 当x的维度=3的时候,f(x) 表示3维空间中的一个平面,当x的维度=n > 3的时候,表示n维空间中的超平面
一个很直观的感受是,让这条直线到给定样本中最近的点最远分的最好,这句话读起来比较拗口,下面给出几个图,来说明一下:


这两种分法哪个更好呢?很明显第二种分的更加明显。
就像我们平时判断一个人是男还是女,就是很难出现分错的情况,这就是男、女两个类别之间的间隙非常的大导致的,让我们可以更准确的进行分类。在SVM中,称为Maximum Marginal,是SVM的一个理论基础之一。选择使得间隙最大的函数作为分割平面是有很多道理的,比如说从概率的角度上来说,就是使得置信度最小的点置信度最大(听起来很拗口),也就是说最近的点分的最开,从实践的角度来说,这样的效果非常好。上图被红色和蓝色的线圈出来的点就是所谓的支持向量(support vector)。
线性可分支持向量机
针对线性可区分,求超平面推导
超平面的公式可以定义为 : W * X + b = 0 W表示权重向量 W={w1,w2,w3,w4.....,wn},n为特征值的个数 , X为训练实例, b表示偏移量
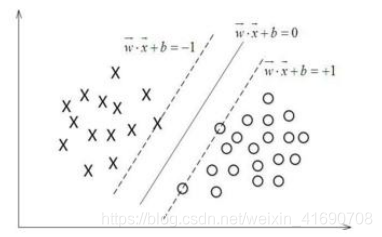
数学建模
求解这个"决策面"的过程,就是最优化。一个最优化问题通常有两个基本的因素:1)目标函数,也就是你希望什么东西的什么指标达到最好;2)优化对象,你期望通过改变哪些因素来使你的目标函数达到最优。在线性SVM算法中,目标函数显然就是那个"分类间隔",而优化对象则是决策面。所以要对SVM问题进行数学建模,首先要对上述两个对象("分类间隔"和"决策面")进行数学描述。按照一般的思维习惯,我们先描述决策面。
数学建模的时候,先在二维空间建模,然后再推广到多维。

根据距离公式

现在,将直线方程扩展到多维,求得我们现在的超平面方程,对公式进行如下变形:
这个d就是"分类间隔"。其中||w||表示w的二范数,求所有元素的平方和,然后再开方。比如对于二维平面:
那么,
目标函数
把w1和w2看成一个向量,x1,x2也是一个向量则有
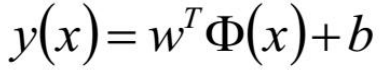
限制条件:|w*x+b|能够相对的表示点x到距离超平面的远近,而w*x+b的符号与类标记y的符号是否一致表示分类是否正确,所以,可以用量y*(w*x+b)的正负性来判定或表示分类的正确性和确信度。
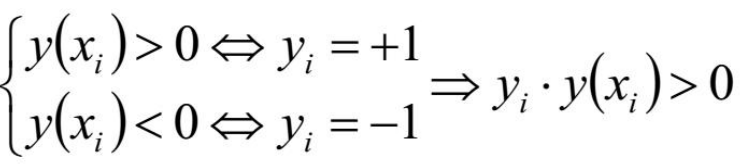
最大间隔分离超平面:
w,b等比例缩放,等价于点到超平面的距离缩放,从而
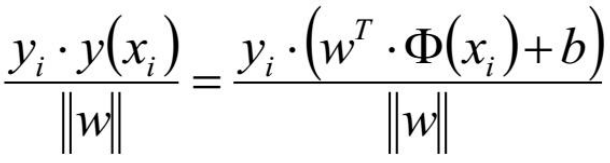
前面已经提到过,让这条直线到给定样本中最近的点最远,即目标函数是
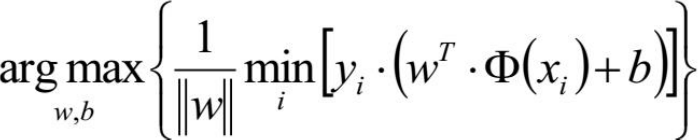
最近的点最远
因为这里的约束条件是支持向量点到超平面的距离为1,即
![]()
到这里,我们前面的问题转化为了求
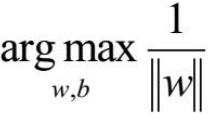
![]()
||w||的意思是w的二范数,跟 表达式是一个意思,之前得到,求SVM的关键就是,最大化这个式子等价于最小化||w||, 另外由于||w||是一个单调函数,为了在进行最优化的过程中对目标函数求导时比较方便,我们可以对其加入平方,和前面的系数。
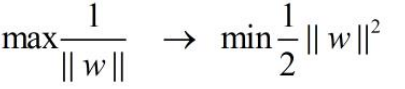
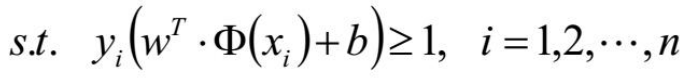
转化为对偶问题,并优化求解:
这个优化问题可以用拉格朗日乘子法去解,使用了KKT条件的理论,这里直接作出这个式子的拉格朗日目标函数:
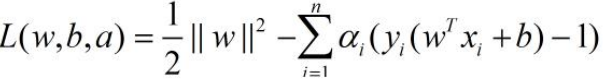
求解这个式子的过程需要拉格朗日对偶性的相关知识
原问题是极小极大问题
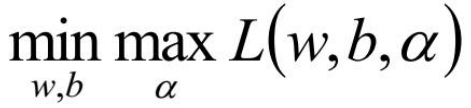
问题的对偶问题,是极大极小问题
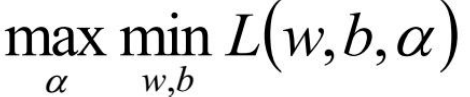
通过拉格朗日函数
首先让L关于w,b最小化,分别令L关于w,b的偏导数为0,得到关于原问题的一个表达式
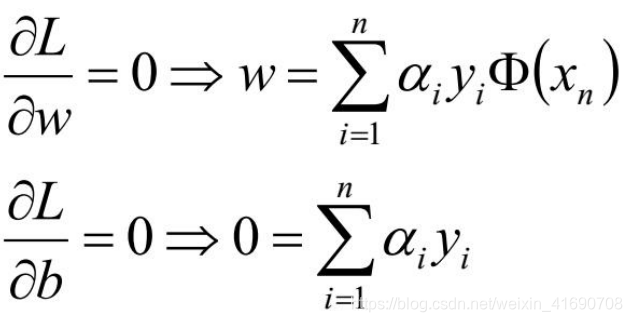
推导过程如下:
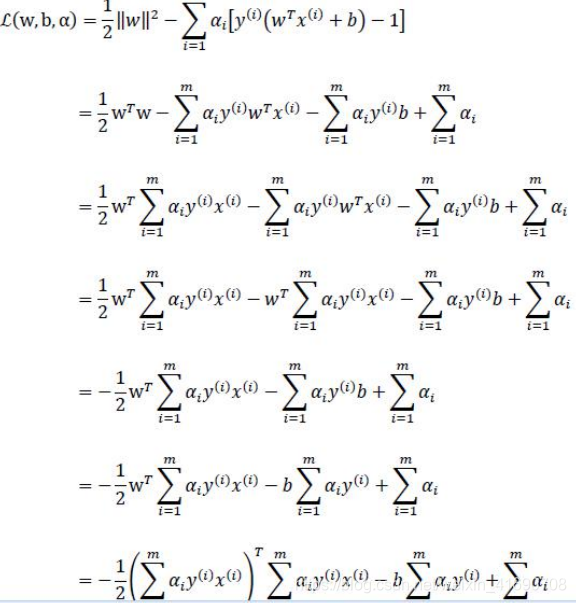

结果加个负号得到
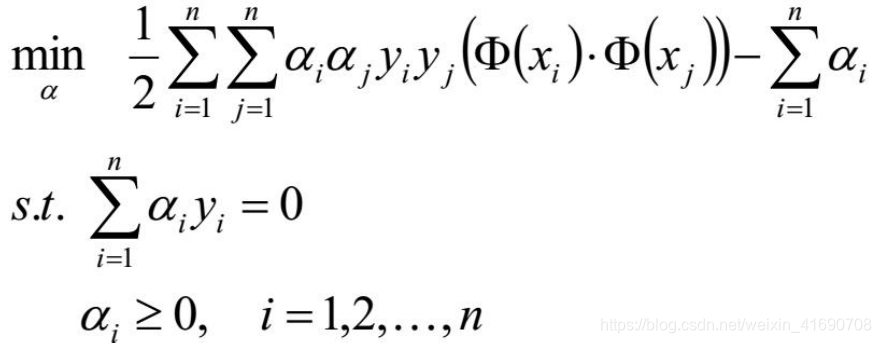

线性不可分
线性可区分(linear separable)和线性不可区分(linear inseparable)
上面是线性可区分的,很容易找到一个超平面将数据分割成两类,但如果不能直接划分出来呢?

线性支持向量机
若是存在离群点呢?如果使用实线来划分,拟合的精度会高一些,但是模型的泛化能力会很差,即测试的时候出现误差过大,即过拟合,这时候我们就需要适当的允许一些离群的点可以超出边界,就是图中的虚线。
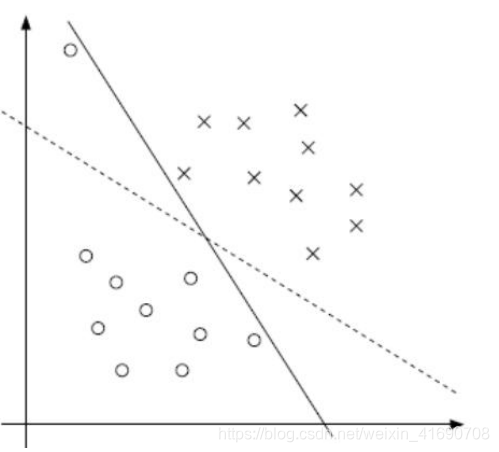
我们知道所有数都不那么干净,不能100%线性可分。我们可以通过引入松弛变量,来允许有些数据点可以处于分割面的错误的一侧
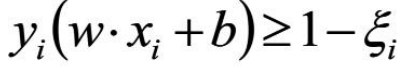
需要加一个松弛因子 ξi≥0
目标函数:
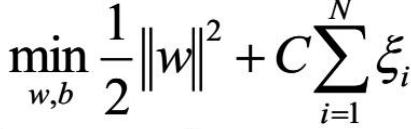
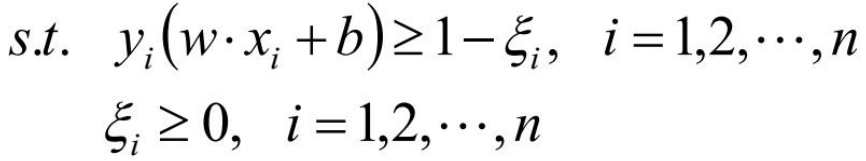
拉格朗日函数:
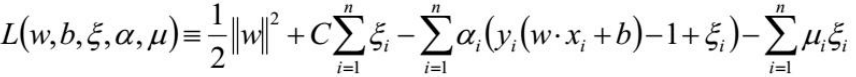
C代表惩罚系数,即如果某个x是属于某一类,但是它偏离了该类,跑到边界上后者其他类的地方去了,C越大表明越不想放弃这个点,边界就会缩小(sklearn里面默认是1)
接下来就是同样的,求解一个拉格朗日对偶问题,得到一个原问题的对偶问题的表达式:
对 求偏导:
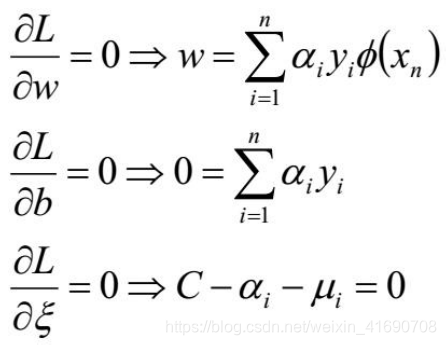
带入得:
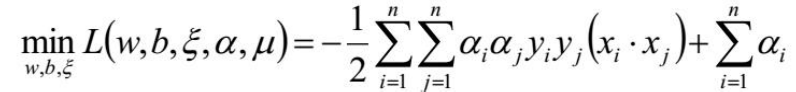
求极大得:

整理得:
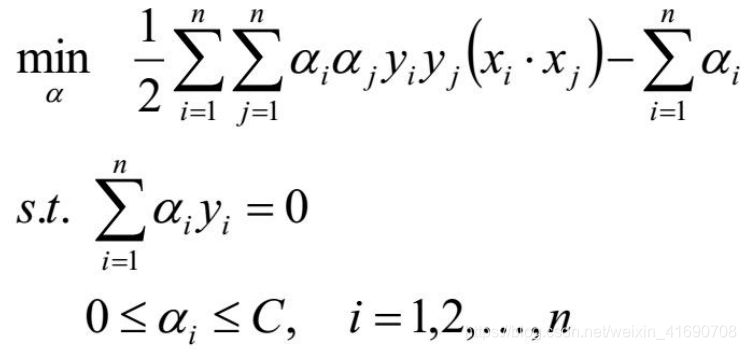
的取值范围是与线性可分的对偶问题表达式的不同之处。在线性不可分情况下得到的对偶问题,不同的地方就是α的范围从[0, +∞),变为了[0, C],增加的惩罚ε没有为对偶问题增加什么复杂度。
求对

(不得不提醒下读者:经过上面第一个步骤的求w和b,得到的拉格朗日函数式子已经没有了变量w,b,只有


 ,即可求出w。然后通过
,即可求出w。然后通过 ,即可求出b )怎么求对偶变量
,即可求出b )怎么求对偶变量

核函数Kernel
事实上,大部分时候数据并不是线性可分的,这个时候满足这样条件的超平面就根本不存在。在上文中,我们已经了解到了SVM处理线性可分的情况,那对于非线性的数据SVM如何处理呢?对于非线性的情况,SVM 的处理方法是选择一个核函数 κ,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。具体来说,在线性不可分的情况下,支持向量机首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面,从而把平面上本身不好分的非线性数据分开。
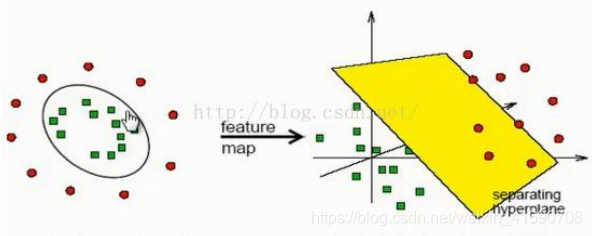
核函数
定理:任意两个样本点在扩维后的空间的内积,如果等于这两个样本点在原来空间经过一个函数后的输出,那么这个函数就叫核函数。
公式:

常用的几个核函数:
线性核:

优点:
- 方案首选,奥卡姆剃刀定律
- 简单,可以求解较快一个QP问题
- 可解释性强:可以轻易知道哪些feature是重要的
限制:只能解决线性可分问题
多项式核:

基本原理:依靠升维使得原本线性不可分的数据线性可分;
升维的意义:使得原本线性不可分的数据线性可分;
优点:
- 可解决非线性问题
- 可通过主观设置幂数来实现总结的预判
缺点:
- 对于大数量级的幂数,不太适用
- 比较多的参数要选择
通常只用在已经大概知道一个比较小的幂数的情况
例如:

高斯核函数 RBF:
优点:
- 可以映射到无限维
- 决策边界更为多样
- 只有一个参数,相比多项式核容易选择
缺点:
- 可解释性差(无限多维的转换,无法算w)
- 计算速度比较慢(解一个对偶问题)
- 容易过拟合(参数选不好时容易overfitting)
- 采用Sigmoid函数作为核函数时,支持向量机实现的就是一种多层感知器神经网络,应用SVM方法,隐含层节点数目(它确定神经网络的结构)、隐含层节点对输入节点的权值都是在设计(训练)的过程中自动确定的。而且支持向量机的理论基础决定了它最终求得的是全局最优值而不是局部最小值,也保证了它对于未知样本的良好泛化能力而不会出现过学习现象。
-
在实战中更多的是:
- 特征维数高选择线性核
- 样本数量可观、特征少选择高斯核(非线性核)
- 样本数量非常多选择线性核(避免造成庞大的计算量)
SVM学习问题可以表示为凸优化问题,因此可以利用已知的有效算法发现目标函数的全局最小值
核函数与之前计算的区别:
1、一个是映射到高维空间中,然后再根据内积的公式进行计算;
2、而另一个则直接在原来的低维空间中进行计算,而不需要显式地写出映射
后的结果。
我们把这里的计算两个向量在隐式映射过后的空间中的内积的函数叫做核函数(Kernel Function)
核函数的本质:
实际中,我们会经常遇到线性不可分的样例,此时,我们的常用做法是把样例特征映射到高维空间中去(如上文的那幅图所示,映射到高维空间后,相关特征便被分开了,也就达到了分类的目的)。但进一步,如果凡是遇到线性不可分的样例,一律映射到高维空间,那么这个维度大小是会很高。此时,就需要核函数,核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数它事先在低维上进行计算,而将实质上的分类效果表现在了高维上,也就如上文所说的避免了直接在高维空间中的复杂计算。
SVM有如下主要几个特点:
(1) 非线性映射是SVM方法的理论基础,SVM利用内积核函数代替向高维空间的非线性映射;
(2) 对特征空间划分的最优超平面是SVM的目标,最大化分类边际的思想是SVM方法的核心;
(3) 支持向量是SVM的训练结果,在SVM分类决策中起决定作用的是支持向量。
(4) SVM 是一种有坚实理论基础的新颖的小样本学习方法。它基本上不涉及概率测度及大数定律等,因此不同于现有的统计方法。从本质上看,它避开了从归纳到演绎的传统过程,实现了高效的从训练样本到预报样本的“转导推理”,大大简化了通常的分类和回归等问题。
(5) SVM 的最终决策函数只由少数的支持向量所确定,计算的复杂性取决于支持向量的数目,而不是样本空间的维数,这在某种意义上避免了“维数灾难”。
(6) 少数支持向量决定了最终结果,这不但可以帮助我们抓住关键样本、“剔除”大量冗余样本,而且注定了该方法不但算法简单,而且具有较好的“鲁棒”性。这种“鲁棒”性主要体现在:
①增、删非支持向量样本对模型没有影响;
②支持向量样本集具有一定的鲁棒性;
③有些成功的应用中,SVM 方法对核的选取不敏感
(7) SVM学习问题可以表示为凸优化问题,因此可以利用已知的有效算法发现目标函数的全局最小值。而其他分类方法(如基于规则的分类器和人工神经网络)都采用一种基于贪心学习的策略来搜索假设空间,这种方法一般只能获得局部最优解。
(8) SVM通过最大化决策边界的边缘来控制模型的能力。尽管如此,用户必须提供其他参数,如使用核函数类型和引入松弛变量等。
(9) SVM在小样本训练集上能够得到比其它算法好很多的结果。支持向量机之所以成为目前最常用,效果最好的分类器之一,在于其优秀的泛化能力,这是是因为其本身的优化目标是结构化风险最小,而不是经验风险最小,因此,通过margin的概念,得到对数据分布的结构化描述,因此减低了对数据规模和数据分布的要求。SVM也并不是在任何场景都比其他算法好,对于每种应用,最好尝试多种算法,然后评估结果。如SVM在邮件分类上,还不如逻辑回归、KNN、bayes的效果好。
(10) 它基于结构风险最小化原则,这样就避免了过学习问题,泛化能力强。
(11) 它是一个凸优化问题,因此局部最优解一定是全局最优解的优点。
(12) 泛华错误率低,分类速度快,结果易解释
不足之处:
(1) SVM算法对大规模训练样本难以实施
SVM的空间消耗主要是存储训练样本和核矩阵,由于SVM是借助二次规划来求解支持向量,而求解二次规划将涉及m阶矩阵的计算(m为样本的个数),当m数目很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间。针对以上问题的主要改进有有J.Platt的SMO算法、T.Joachims的SVM、C.J.C.Burges等的PCGC、张学工的CSVM以及O.L.Mangasarian等的SOR算法。
如果数据量很大,SVM的训练时间就会比较长,如垃圾邮件的分类检测,没有使用SVM分类器,而是使用了简单的naive bayes分类器,或者是使用逻辑回归模型分类。
(2) 用SVM解决多分类问题存在困难
经典的支持向量机算法只给出了二类分类的算法,而在数据挖掘的实际应用中,一般要解决多类的分类问题。可以通过多个二类支持向量机的组合来解决。主要有一对多组合模式、一对一组合模式和SVM决策树;再就是通过构造多个分类器的组合来解决。主要原理是克服SVM固有的缺点,结合其他算法的优势,解决多类问题的分类精度。如:与粗集理论结合,形成一种优势互补的多类问题的组合分类器。
(3)对缺失数据敏感,对参数和核函数的选择敏感
支持向量机性能的优劣主要取决于核函数的选取,所以对于一个实际问题而言,如何根据实际的数据模型选择合适的核函数从而构造SVM算法.目前比较成熟的核函数及其参数的选择都是人为的,根据经验来选取的,带有一定的随意性.在不同的问题领域,核函数应当具有不同的形式和参数,所以在选取时候应该将领域知识引入进来,但是目前还没有好的方法来解决核函数的选取问题.
支持向量机的主要应用和研究的热点
目前支持向量机主要应用在模式识别领域中的文本识别,中文分类,人脸识别等;同时也应用到许多的工程技术和信息过滤等方面.
当前研究的热点主要是对支持向量机中算法的优化,包括解决SVM中二次规划求解问题,对大规模SVM的求解问题,对SVM中QP问题的求解问题等.另外就是如何更好的构造基于SVM的多类分类器,如何提高SVM的归纳能力和分类速度等.如何根据实际问题确定核函数也是一个重要的研究热点.





 本文深入探讨了支持向量机(SVM)的基础知识,包括线性分类器、数学建模、线性不可分情况的处理以及核函数的作用。SVM通过最大化分类间隔来寻找最优超平面,以实现良好的分类效果。然而,SVM在处理大规模数据集、多分类问题和缺失数据时面临挑战,对参数和核函数的选择敏感。SVM广泛应用于模式识别和工程领域,研究热点包括算法优化、多类分类器构建和核函数选择。
本文深入探讨了支持向量机(SVM)的基础知识,包括线性分类器、数学建模、线性不可分情况的处理以及核函数的作用。SVM通过最大化分类间隔来寻找最优超平面,以实现良好的分类效果。然而,SVM在处理大规模数据集、多分类问题和缺失数据时面临挑战,对参数和核函数的选择敏感。SVM广泛应用于模式识别和工程领域,研究热点包括算法优化、多类分类器构建和核函数选择。


















 8879
8879

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








