对于机器学习主要分为两大类型,第一类分类,第二类回归,当然针对不同类型的算法问题,评估模型的好坏的指标也不相同。接下来我针对两类进行机器学习模型指标的大致介绍。
1 分类指标
关于分类器模型中又分为二分类和多分类
对于二分类问题模型预测的类别要么正类要么负类,那么可以分为真正类,假正类,要么真负类,假负类。可以使用二元混淆矩阵表示。
|
|
真实类别 | ||
|
1(Positive)正例 |
0(Negative)负例 | ||
|
预测类别 |
1(Positive) 正例 |
TP(True Positive)真正例 |
FP(False Positive)假正例 |
|
0(Negative) 负例 |
FN(False Negative)假负例 |
TN(True Negative)真负例 | |
根据分类混淆矩阵我们可以得出二分类模型评价指标:accuracy(准确率)、precision(精准率)、recall(召回率)、F1-Score
(1) accuracy(准确率) 指的是正确预测的样本数/总数 (TP+TN)/(TP+FP+TN+FN) 打比方医生通过医学手段预测一个人是否得癌症,医生做的判别和实际病人相同在所有病人的比例,可以判断出这个医生的准确率,当然越高越好。
(2) precision(精准率) 指的是正确预测的正例数 /预测正例总数 TP /TP+FP 医生正确预测没有得癌症的人占他所预测没有癌症的人中比例
(3)recall (召回率) 也叫查全率,表现在实际正样本中,分类器能预测出多少正确正例数,即正确预测的正例数 /实际正例总数,公式表示为Recall = TP/(TP+FN)。
(4)F1-Score是精确率和召回率的调和值,更接近于两个数较小的那个,所以精确率和召回率接近时,F值最大。很多推荐系统的评测指标就是用F值的。2/F1 = 1/Precision + 1/Recall
关于曲线相关指标
PR曲线的横坐标是精确率P,纵坐标是召回率R。显然精确率和召回率都是越大越好,即在上方的曲线比下方的曲线好。当精确率和召回率接近时F1Score最大,因此也可以直接找F1score的最大点(只需要画直线y=x)。
ROC 曲线
根据ROC曲线分出:
真正率(True Positive Rate,TPR):TPR=TP/(TP+FN),即被预测为正的正样本数 /正样本实际数。
假正率(False Positive Rate,FPR):FPR=FP/(FP+TN),即被预测为正的负样本数 /负样本实际数。
假负率(False Negative Rate,FNR) :FNR=FN/(TP+FN),即被预测为负的正样本数 /正样本实际数。
真负率(True Negative Rate,TNR):TNR=TN/(TN+FP),即被预测为负的负样本数 /负样本实际数。
分母都是根据分子是否为真或为假,定正样本还是负样本的实际数
ROC(Receiver Operating Characteristic)曲线在对于正负例的判断中,我们会设置一个阈值,当大于这个阈值则为正例,小于这个阈值则为负例,根据不同的阈值,采用横坐标为False Positive Rate(FPR假正率),纵坐标为True Positive Rate(TPR真正率),便可做出ROC曲线。对角线对应的是随机猜测的表现,一般曲线越接近左上角,则分类器的性能越好,就是真正率越高,假正率越低时效果越好。
ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。
AUC 为ROC曲线所覆盖的区域面积,显然,AUC越大,分类器分类效果越好。当AUC=0.5,则表示为随机猜测,没有预测价值,当AUC>0.5优于随机猜测,当AUC<0.5比随机猜测还差,但只要反预测便可优于随即猜测。AUC的物理意义是任取一个正例和任取一个负例,正例排序在负例之前的概率。所以取值范围(0.5 -1)之间
R方待补充。。。。
2 回归问题模型判别指标
(1) MSE(Mean squared error)均方误差 预测值与实际值差值平方累和取平均 差的平方的和的平均
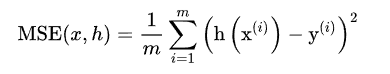
(2)RMSE(均方根误差),顾名思义,这就是MSE开方根,实质也一样,不过对于很大的数据可以较好的比较。测量预测向量与目标值向量之间的距离,又称为欧几里得范数,L2范数
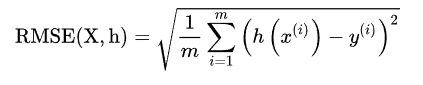
(3)MAE(平方绝对误差),作用类似于MSE,只要想到最小二乘法就好了。计算绝对值的总和,对应于L1范数,又称为曼哈顿距离
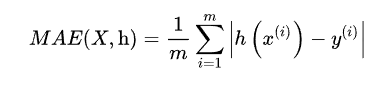





 本文详细介绍了机器学习中分类和回归模型的评估指标。包括准确率、精准率、召回率、F1-Score等分类指标,以及MSE、RMSE、MAE等回归指标。并解释了ROC曲线、AUC值的概念及其在模型评估中的应用。
本文详细介绍了机器学习中分类和回归模型的评估指标。包括准确率、精准率、召回率、F1-Score等分类指标,以及MSE、RMSE、MAE等回归指标。并解释了ROC曲线、AUC值的概念及其在模型评估中的应用。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








