本文深入探讨了全频域平均功率的间接法和直接法，分析了非参数化估计方法中的周期图、相关图及Blackman-Tukey方法。通过对比周期图、Blackman-Tukey、Bartlett、Welch和Daniell法，总结了经典谱估计的优缺点，如分辨率受限、谱泄露和方差性能不佳等问题。
4.1.1 间接法
全频域的平均功率：
4.1.2 直接法
此二种定义当
时等价，此时意味着
衰减的足够快。
谱估计的问题在于：已知一个有限长序列
，求PSD理论值
的估计值
，其中
。
4.2 非参数化估计方法
4.2.1 Periodogram周期图
可以看出，这是第二种定义方法在序列长度N有限，试验次数有限（非期望）条件下的实际值。
4.2.2 Correlogram 相关图
可以看出，这是第一种定义方法在序列长度N有限条件下的实际值。
因为序列长度N有限所以得到的相关函数并非真实值，而是估计值
。
4.2.3 两种的估计方法
4.2.3.1 无偏估计
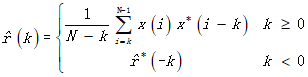
证明：是的无偏估计
l 当k较大时，无偏对的估计越来越差，很大而且不稳定，因为在这种情况下估值仅仅是通过几个乘积的平均得到的。
l 由无偏估计求出来的功率谱
可能
0.
4.2.3.2 有偏估计
证明：是的渐近无偏估计
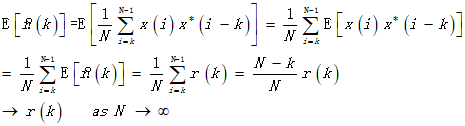
l 有偏估计求出来的功率谱
l 相关矩阵的估计
是半正定的
计算
可以使用20世纪最伟大的算法之一FFT。
4.2.4 回顾FFT
DFT计算复杂度为
：
令
，
其中，
所以
这个分解过程要持续进行，直到两个点的FFT为止。整个过程需要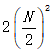
次复数乘法。
l 一个点的FFT算法的计算复杂度为
l 可以通过补零运算使点数
l 补零不改变
的分辨率
4.2.5 周期图和相关图的特性
由周期图和相关图估计的是不尽人意的，因为和都来自于随机过程的一次实现。周期图谱估计器和相关图谱估计器具有等价性，因此可以同时推导他们的特性。
当是有偏估计时
由于
时，
时，
所以
这相当于使用长度为（2N-1）的Bartlett（三角窗）对进行截断。
Bartlett窗
Bartlett窗频域以及主瓣3DB带宽
令
，为理想功率谱
l 
主瓣的作用是平滑，对存在尖峰的带来的影响要大于对平坦带来的影响，而且若
（白噪声），则周期图法是无偏估计器
；
l 旁瓣使主板对应频率中的能量泄漏到旁瓣所在频率中去；
l 中相邻谱峰举例小于
时，对应谱峰在周期图中无法被分辨；
l 称为角频率下周期图谱分辨率极限；
l 随着
，的偏差（BIAS）减小，渐近无偏。
当是无偏估计时
相当于使用长度为（2N-1）的矩形窗对进行截断
矩形窗
经典谱估计中周期图的问题主要不在于偏差问题，因为若仅仅是偏差问题，那么增加序列长度N就可以消除其偏差，其主要的问题是方差大而且分辨率不行，是渐近无偏但不一致的估计，标准差等于真实PSD的值，即使样本增加到无限大，方差也不等于0.
下面将会看到改进方法将以增加偏差或降低分辨率为代价来降低方差。
4.2.6 Blackman-Turkey （BT）方法
其中
叫做延时窗
l BT谱估计器是周期图的局部加权平均
l M值越小，
的分辨率越差，但方差随着M值减小而降低。
l 的分辨率
l 的方差
，对于固定的M来说，是渐近有偏并且方差à0
因为
，所以很自然地也要求
，这一特性可以通过选择合适的延迟窗达到。
证明：如果延迟窗
是半正定的，则加窗的协方差矩阵序列
也是半正定的。
由
组成的矩阵
若是半正定的，或者说是半正定序列，则y的DTFT
因此，要使，当且仅当下面所有维数的Toeplitz矩阵都是半正定的
其中
表示Hadamard矩阵乘积（也就是对应元素的乘积），由矩阵分析可知，两个半正定矩阵的Hadamard乘积仍然是半正定的。
所以可以发现，若 是有偏估计，
，那么若
则。
l 非负定（半正定）窗有：Bartlett、Parzen
4.2.7 窗函数时间-带宽积
绝大多数窗在时域和频域都呈现非负性，如果他们有负制，那么这些值要比它们的正值小很多，另外，在时域和频域它们的峰值均出现在坐标原点。对于这一类窗，其等效时宽
和等效带宽
定义如下：
根据离散时间序列的正、逆DTFT定义，
可以得出（等效）时间-带宽乘积：
上述结果用在类似于窗函数的信号中，可以看出，窗函数不能既时限，又带限，窗函数在一个域衰减至0的速度越慢，则在另一个域内分布越集中。
4.2.8 窗的设计与选择
由于谱分辨率范围大约应为1/M，方差与M/N成正比，M是窗长。因此要考虑分辨率-方差的折中。
有如下结论：
l 窗的长度应在谱分辨率和统计方差之间折中选择
l 窗的形状应在谱的平滑和泄漏之间折中考虑
l 
l 窗形状要保证
4.2.9 Blackman-Tukey类其他非参数谱估计
4.2.9.1 Bartlett方法
Bartlett方法的思想很简单，即：将具有N个观测点的可用样本分成L=N/M个子样本，每个子样本有M个观测点，然后再每个
值上对所有子样本的周期图进行平均，以此来减小周期图中较大的波动。
是一个N点序列，
是M点序列，且
是非重叠的，
Bartlett方法是对长为M的分段数据进行计算，其分辨率大约为
。可见，与原始周期图方法相比，Bartlett方法的分辨率下降了L倍。
因为
其中，
为对应于第l个子样本的样本协方差序列，将上式代入Bartlett功率谱分段求平均的式子中。可得：
可见
在形式上与使用长度为M的矩形窗的BT法相似，但Bartlett的方差稍大，因为当
时，延迟积中只有1个又来完成对
的估计，且因为Bartlett使用了一个固定的矩形延迟窗，因此其在分辨率-频谱泄漏的折中上要比BT法要差。
和基本的周期图相比，Bartlett估计的分辨率降低了，又因为其对ACS（autocovariance sequence）做了L次平均，所以方差也下降了，下降的倍数均为L=N/M。
因为Bartlett估计使用的是矩形窗，因此其对谱的平滑能力最弱，分辨率最高，但泄漏也最大。
4.2.9.2 Welch 方法
和Bartlett方法的区别是，在Welch方法中可以重叠，
，并且可以加不同的窗
令窗w的功率为
，用来对加窗后的功率谱进行归一化。
因为可以重叠，我们希望重复利用的数据越多越好，因此通常选择一个较大的S，Welch在论文中建议选50%的重叠率。在实际工程中，
能提供略低于的方差，低的不是特别显著。Welch法增加了周期图平均的次数，且为了更好的控制PSD方差-分辨率特性，所以在计算周期图中引入了不同的时间窗，且时间窗对每一个M点子样本序列末端数据的加了较小的权重，使得即使子序列重叠，彼此加窗后的相关性也较小。
4.2.9.3 Daniell方法
由于不同频率点处的周期图值是渐近不相关的随机变量，可以考虑以当前频率 为中心的小区间对周期图平均，以此来减小基本周期图估计器的大的方差。
从上式可见，随着
的增大，Daniell估计器的分辨率下降（因此偏差增大），方差随之减小。
并将上式与BT估计器
对比可知，Daniell估计器是BT法的特例，即对应矩形频谱窗的情况：
4.2.10 仿真对比各种经典谱估计方法
为了对比这几种方法的优缺点，在仿真的程序中保持分析的信号不变，分别利用上述的方法进行分析如下时域信号：
l 周期图
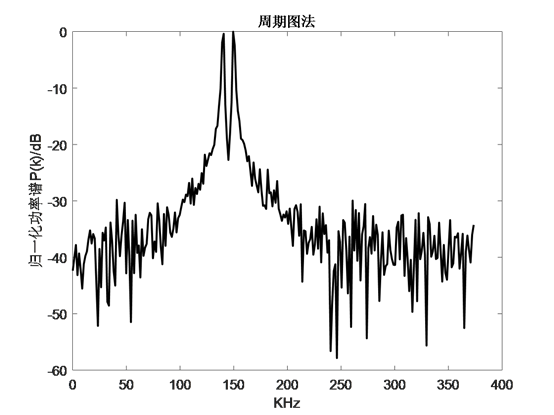
l Blackman-Tukey法
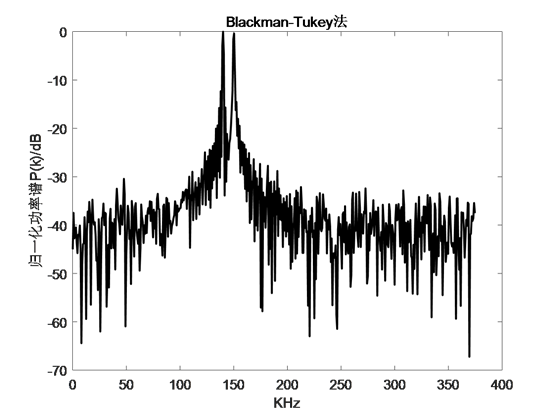
l Bartlett法
l Welch法
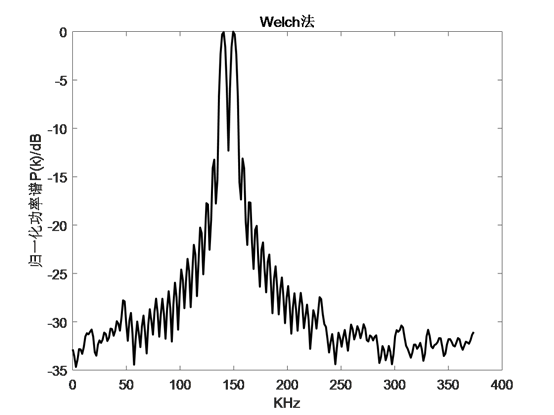
l Daniell法
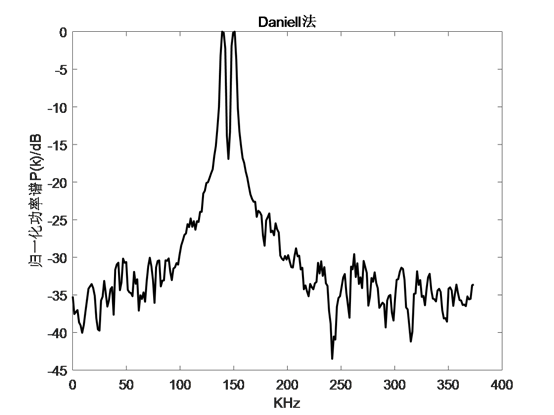
4.2.11 经典谱估计总结
l 经典谱估计可以用FFT快速计算，且物理概念明确，因而仍是目前很常用的谱估计方法。
l 谱的分辨率较低，它正比于，N是所使用的数据长度。
l 由于不可避免的窗函数的影响，使得真正谱在窗口主瓣内的功率向旁瓣部分“泄露”，降低了分辨率。较大旁瓣有可能掩盖中较弱的成分，或是产生假的峰值。当分析的数据较短时，这些影响更为突出。
l 方差性能不好，不是的一致估计，且N增大时谱线起伏加剧。
l 周期图的平滑和平均是和窗函数的使用紧紧相关联的。平滑和平均主要是用来改善周期图的方差性能，但往往又降低了分辨率和增大了偏差。没有一个窗函数能使估计的谱在方差、偏差和分辨率这几个方面都得到改善。因此，使用窗函数只是改进估计质量的一个技巧问题，而不是根本的解决办法。
扫一扫
983
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
