SPF vs Bellman-Ford 图解

原创 已于 2023-06-10 20:12:25 修改 · 1k 阅读 · 3 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #网络 #图论

于 2022-10-07 14:06:07 首次发布
本文详细介绍了SPF算法与Bellman-Ford算法的工作原理及应用场景。SPF算法由荷兰科学家狄克斯特拉提出，是OSPF、IS-IS路由协议的基础；Bellman-Ford算法则适用于存在负权边的情况，能检测负权回路。

SPF算法

百度百科：SPF算法也被称为Dijkstra算法，这是因为最短路径优先算法SPF是由荷兰计算机科学家狄克斯特拉于1959年提出的。
SPF算法将每一个路由器作为根（ROOT）来计算其到每一个目的地路由器的距离，每一个路由器根据一个统一的数据库会计算出路由域的拓扑结构图，该结构图类似于一棵树，在SPF算法中，被称为最短路径树。SPF算法是OSPF、IS-IS路由协议计算最短路径的基础。
在OSPF路由协议中，最短路径树的树干长度，即OSPF路由器至每一个目的地路由器的距离，称为OSPF的Cost，其算法为：Cost = 100Mbps/链路带宽。

参考文章

SPF（Dijkstra）算法完美教程
ospf学习-----SPF最短路径算法

SPF案例

如图，V0~V8是9台路由器节点，节点之间的值是cost开销值的大小，我们以V0节点作为根，计算到其他节点的最短路径，也就是在V0看来去往其他节点最近的路径。
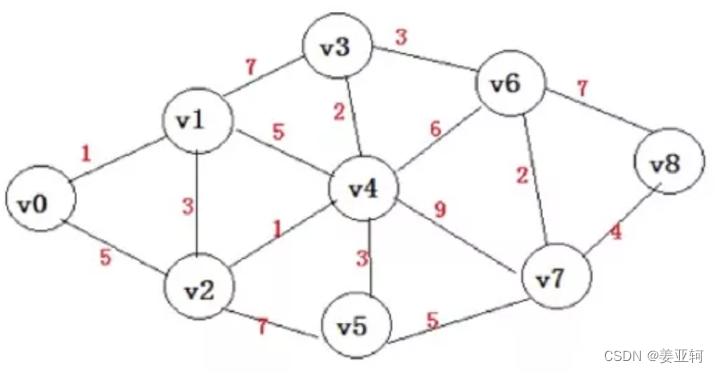
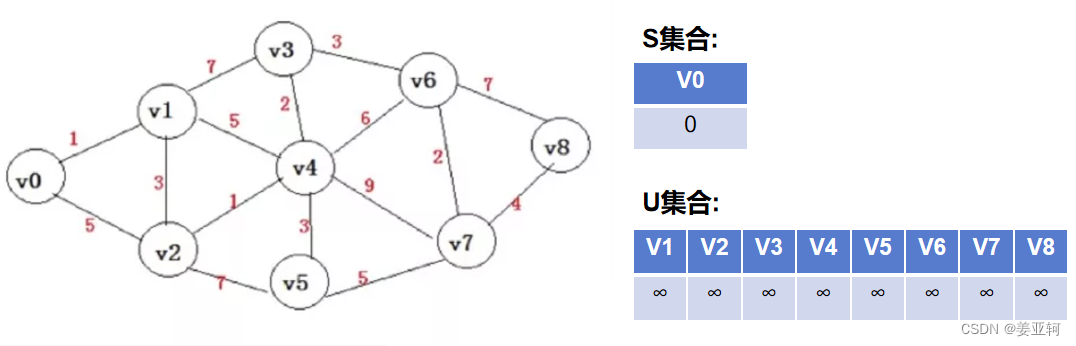
在这里插入图片描述
我们创建两个集合，分别是：
S集合：每求得一条最短路径 , 就将其节点加入到集合S中，直到全部顶点都加入到S时，算法就结束，初始时S中只有一个源点V0，且自己到自己的cost为0
U集合：其余未确定最短路径的顶点集合，初始时U中有除V0以外的所有节点，且从V0到其他所有节点的cost为无穷
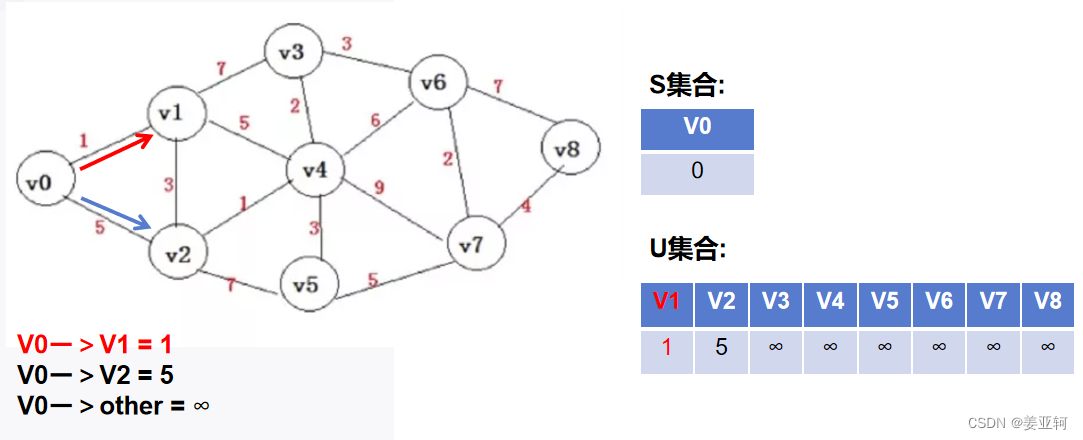
在这里插入图片描述

第一次，我们先从V0开始发散，V0与V1、V2直连的cost值分别是1和5，与其他节点不直连所以cost设为无穷大，因为V0->V1的cost值在U集合中最小，所以将V1标红并加入到S集合当中
在这里插入图片描述

第二次，我们从V1开始发散，V1与V2、V3、V4

最低0.47元/天 解锁文章
（3-1）Bellman-Ford算法：Bellman-Ford算法介绍
码农三叔
02-11 1342
Bellman-Ford算法是一种用于寻找图中单源最短路径的算法，可以处理带有负权边的图。它通过对所有边进行松弛操作来逐步更新节点的最短路径估计，最多进行|V|-1次迭代，其中|V|是节点数。如果在这些迭代中仍然存在可更新的最短路径，则说明图中存在负权环。算法的时间复杂度为O(V*E)，其中V是节点数，E是边数。在本章的内容中，将详细讲解Bellman-Ford算法在路径规划中的用法，展示这些算法在智能驾驶、无人机和机器人领域中的应用过程。
（3-3）Bellman-Ford算法：Bellman-Ford算法的应用案例
码农三叔
07-08 1066
在这个特定的例子中，由于图中存在负权边，因此可能会出现路径的分叉，这是因为Bellman-Ford算法可以通过负权边找到更短的路径。我们将使用一个模拟的场景：一辆汽车需要穿越城市之间的道路网络，每条道路都有一个特定的距离（有可能是负数，代表着某些道路是陡坡下坡），我们需要找到汽车从起点到终点的最短路径。（1）首先，定义了一个Graph类和一个Edge类，其中类Graph使用networkx库来表示城市道路网络，每个节点代表一个路口，每条边代表两个路口之间的道路，边的权重表示车辆通过该道路所需的时间。
SPF算法
qq_62567244的博客
02-23 3673
拓扑图AR10与AR11之间用点到点网络连接 以AR10为根节点构建SPF结构拓扑图 先查看AR10自身发送的一类LSA，将传输网络（TransNet）点到点（P-2-P）类型添加到候选列表中选取其中最小开销的节点作为下一连接节点 再查看DR接口100.12.10.12发送的二类LSA,将未出现在拓扑图中的Router添加进候选列表中，开销值为0，再从列表中选取最小开销值的节点作为下一连接节点 查看下一节点的一类LSA，继续将未出现在拓扑图中的节点添加进候选列表...
最短路问题 Bellman-Ford（单源最短路径）(图解)
m0_63658130的博客
04-27 8268
最短路问题 Bellman-Ford 单源最短路径 图解
SPF算法用于计算到达网络中各目的地最短路径的核心算法
最新发布
weixin_42185241的博客
10-23 399
在P2P网络中，SPF计算与广播网络的主要区别是没有Network-LSA（Type 2）参与，整个SPF计算完全基于Router-LSA（Type 1）进行。SPF树：{R2→R4, Cost=10;R2的LSDB: [R1-LSA, R2-LSA, R3-LSA, Network-LSA...]R1的LSDB: [R1-LSA, R2-LSA, R3-LSA, Network-LSA...]R3的LSDB: [R1-LSA, R2-LSA, R3-LSA, Network-LSA...]
OSPF的基本工作原理
bying666的博客
07-18 5247
OSPF的基本工作原理 1.定义 2.特点 3.基本概念 4.OSPF五种分组类型 5.DR/BDR 6.区域 1.定义 开放最短路径优先OSPF，是为了克服RIP的缺点在1989年开发出来的。 “开放” 表明OSPF协议不是受某一家产商控制，而是公开发表的。 “最短路径优先”是因为使用了dijkstra提出的最短路径算法SPF。 2.特点 ①OSPF–>基于链路状态，而不是RIP–>基于距离向量 ②OSPF采用SPF算法计算路由，从算法上保证了不会发生路由环路。 ③OSPF不限制网络的规模
SPF（连通图---求割点）
nhl19961226的博客
01-20 403
题目链接：SPF 题目大意：给你n条边，问哪条边将网路分成了几个子网络（输出所有的情况）。 思路：给你的是无向图，直接上求割点的模板。 代码： #include #include #include #include using namespace std; const int maxn=2009; int dfs_clock,DFN[maxn],cut[maxn],low[maxn]
poj 1523 SPF 图论基础 图的割点
ned_chu的博客
09-10 1131
图论基础 图的割点
精选资源
Neural Bellman-Ford Networks A General Graph Neural Network Fra
10-09
在【NeurIPS 2021】会议论文“Neural Bellman-Ford Networks: A General Graph Neural Network Framework for Link Prediction”中，作者们提出了一个新的框架——神经Bellman-Ford网络（NBFNet），这是一种用于链路...
图解Bellman-Ford算法
04-13
**标题：“图解Bellman-Ford算法”** **正文：** Bellman-Ford算法是一种用于解决最短路径问题的图算法，特别是在存在负权边的情况下。这个算法由Richard Bellman在1958年提出，后来由Ford进一步发展和完善。在...
图详解第五篇：单源最短路径--贝尔曼-福特(Bellman-Ford)算法
m0_70980326的博客
10-20 8459
单源最短路径--Bellman-Ford算法（可处理带负权路径的图）
OSPF篇——SPF算法——002
里晓山的博客
06-10 3402
目录最短路径优先算法 SPF阶段1：构建SPF树阶段2：计算最优路由在一类LSA和二类LSA中，包括了拓扑信息和路由信息，OSPF将依据SPF算法和各类LSA（LSA内既包含拓扑信息又包含路由信息，但是分开使用的，先使用拓扑信息构建SPF书，在根据网段信息添加路由信息，也就是叶子信息）进行最短路径树计算OSPF SPF算法：先在区域内使用LAS 1和2 flooding（泛洪）--->一致DB--->一致拓扑--->以自己为根--->SPF树--->挂Leaf叶子网络信息--->算路由链路状态的算法要比距离
spf算法概述
SSS
02-24 1万+
文章目录1. 算法概念2. Isis和ospf spf算法实现差异3. 具体计算方法4. spf算法能保证最短路径的原因5. 路由计算 1. 算法概念 Spf：最短路径优先 shortest path first 有向权值图 求取某节点到任意其他节点的最短路径 广度优先算法 2. Isis和ospf spf算法实现差异 Isis使用堆排序，ospf使用排序链表 3. 具体计算方法 拓扑计算 根节点加入候选链表 运行spf算法直到候选链表为空 1.弹出候选链表中cost最小的节点 2.遍历当前处理节点的所有l
学习笔记——动态路由——OSPF工作原理（SPF算法）
灵韵的博客
07-05 3649
RTA将自己添加到最短路径树的树根位置，然后检查自己生成的Router-LSA，对于该LSA中所描述的每一个连接，如果不是一个Stub连接，就把该连接添加到候选列表中，分节点的候选列表为Link ID，对应的候选总开销为本LSA中描述的Metric值和父节点到达根节点开销之和。将节点3.3.3.3，Metric=0，父节点到根节点的开销为2，候选总开销为2，加入候选列表。第三个P-2-P连接中，Link ID为4.4.4.4，Metric=48，父节点到根节点的开销为1，候选总开销为49，加入候选列表。
调度算法概念
m0_52559870的博客
05-17 2663
一、先来先服务 FCFS-first come first serve 1.算法思想 主要从“公平”的角度考虑（类似于我们生活中排队买东西的例子) 2.算法规则 按照作业/进程到达的先后顺序进行服务 3.用于作业/进程调度 用于作业调度时，考虑的是哪个作业先到达后备队列;用于进程调度时，考虑的是哪个进程先到达就绪队列 4.是否可抢占? 非抢占式的算法 5.优缺点 优点:公平、算法实现简单 缺点:排在长作业（进程）后面的短作业需要等待很长时间，带权周转时间很大，对短作业来说用户体验..
操作系统-处理机调度详解（调度层次及FCFS、SPF、RR等算法）
热门推荐
关注网络安全、云原生安全
06-03 4万+
调度层次 1.高级调度（High Level Scheduling)高级调度又称长程调度或作业调度，它的调度对象是作业。主要功能是根据某种算法，决定将外存上处于后备队列中的哪几个作业调入内存，为它们创建进程、分配必要的资源，并将它们放入就绪队列。高级调度主要用于多道批处理系统中，而在分时和实时系统中不设置高级调度。 2.低级调度（Low Level Scheduling)低级调度又称为进程调度或短程调度，其所调度的对象是进程（或内核级线程）。其主要功能是，根据某种算法，决定就绪队列中的哪个进程应获得处理机
【SPF 最短路径优先算法】
叫我小虎就行了的博客
08-12 832
【SPF 最短路径优先算法】
手把手教你手撕SPF生成树(OSPF区域内防环)
好好睡觉
07-25 3252
SPF算法，OSPF区域内防环
算法(五):图解贝尔曼-福特算法
weixin_34187822的博客
08-18 4248
算法简介 贝尔曼-福特算法(Bellman–Ford algorithm )用于计算出起点到各个节点的最短距离，支持存在负权重的情况 它的原理是对图进行最多V-1次松弛操作，得到所有可能的最短路径。其优于迪科斯彻算法的方面是边的权值可以为负数、实现简单，缺点是时间复杂度过高，高达O(VE)。但算法可以进行若干种优化，提高了效率。 Bellman Ford算法每次对所有的边进行松弛，每次松弛...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

姜亚轲

你花钱的样子真帅

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值