算法------（8）二分_路标设置 acwing-优快云博客

文章介绍了如何使用二分搜索策略解决一元三次方程的根查找问题以及设备充电优化问题。作者提到在给定范围内找到满足条件的解，并在特定场景下对二分搜索的应用进行了详细阐述。

例题：（1）Acwing 789.数的范围（2）AcWing 790. 数的三次方根

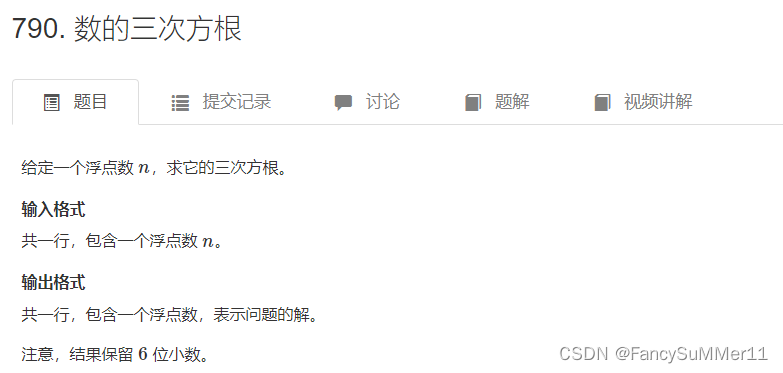
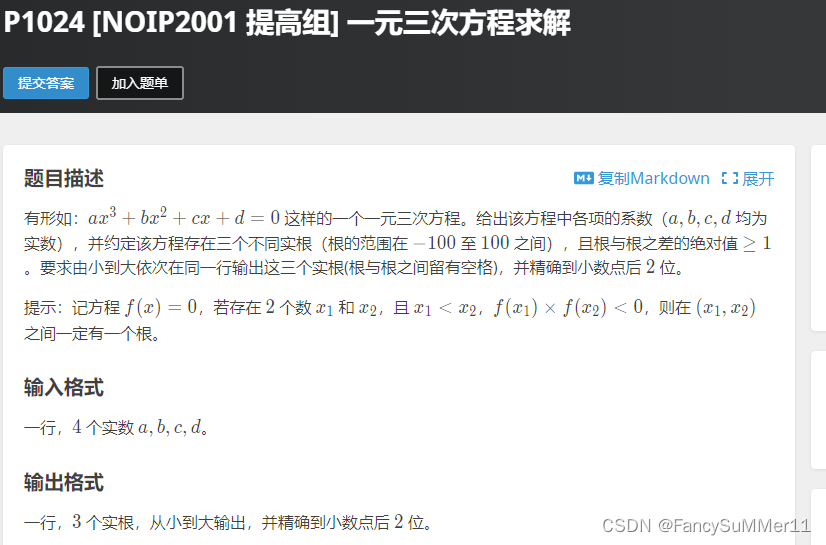
练习：（1） P1024 一元三次方程求解

还是没想到怎么好好利用二分。。。

题目保证根与根之差的绝对值>=1，且方程的根在-100,100之内。因此可以在每一个长度为1的左右端点为整数的区间内寻找解，如果两个端点的函数值一正一负则必有一个解。如果左端点为0则左端点为解。不考虑右端点的原因是两次相邻循环会重复计入，因此只用考虑一个端点即可（除了100.0以外的每一个端点都会成为左端点，因此要对100.0进行特判，不过洛谷数据太水了）。端点内找解用二分就可以。

#include <iostream>
using namespace std; 
double a,b,c,d;
double func(double x){
	return a*x*x*x+b*x*x+c*x+d; 
}
int main(int argc, char** argv) {
	scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
	int sum = 0;
	for(int i = -100;i<100;i++){
		double l = i,r = i+1.0;
		double y1 = func(l),y2 = func(r);
		if(!y1){
			printf("%.2f ",l);
			sum++;
		}
		if(y1*y2<0){
			while(r-l>1e-6){
				double mid = (l+r)/2;
				if(func(mid)*func(l)<0) r = mid;
				else l = mid;
			}
			printf("%.2f ",l);
			sum++; 
		}
		if(sum==3) break;
	}
    if(!func(100.0)) printf("%.2f ",100.0);
	return 0;
}

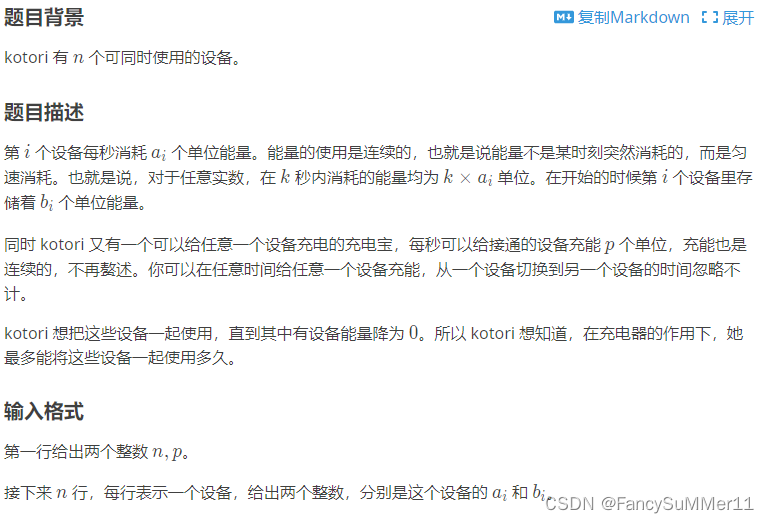
（2）P3743 kotori的设备

没做出来啊啊啊啊。。。

二分时间。。假如总耗电速度小于充电速度则直接输出-1，否则对那些有充电需求的充电宝进行统计，判断在该时间下需要充电的总量和充电宝能提供电的量，然后进行二分操作。

二分右端点起始为1e10，因为设备最多有1e5个，假设每个设备的每秒消耗为1，而充电速度为1e5-1，则每秒会少1e-5的电，因此时间最长就是1e10。

#include <iostream>
using namespace std;
const int N = 1e5+10;
double a[N],b[N]; 
double p,cs = 0,sum = 0;
int n;
bool check(double x){
	double sum = 0;
	for(int i = 0;i<n;i++){
		if(b[i] >= a[i]*x) continue;
		sum += a[i]*x - b[i];
	}
	return sum >= p*x;
}
int main(int argc, char** argv) {
	scanf("%d%lf",&n,&p);
	for(int i = 0;i<n;i++){
		scanf("%lf%lf",&a[i],&b[i]);
		cs += a[i];
	}
	if(cs<=p) printf("-1");
	else{
		double l = 0,r = 1e10+5;
		while(r-l >= 1e-6){
			double mid = (l+r)/2;
			if(check(mid)) r = mid;
			else l = mid;
		}
		printf("%lf",l);
	}
	return 0;
}

(3)P1182 数列分段 Section II 没做出来，又是一个奇妙的二分方式。。

二分最大值的可能值，左端点是该序列的最大值，右端点是数组总和，这个区间就包含了所有可能的结果。而最大值越大的，需要分的区间就越少。因此判断一个数组划成的区间数是否大于题目要求，就可以成为二分中用于判断的性质。

顺便提一嘴。。。P3853 [TJOI2007] 路标设置这道题，二分左端点应该从1开始，因为不存在空旷程度是0的情况。。要注意某个值的实际含义再确定左右端点啊。。。

#include <iostream>
using namespace std;
typedef long long ll; 
const int N = 1e5+10;
int a[N];
int n,m;
bool check(ll x){
	ll sum = 0;
	int cnt = 0;
	for(int i = 0;i<n;i++){
		if(sum+a[i] > x){
			cnt++;
			sum = a[i];
		}
		else{
			sum+=a[i];
		}
	}
	if(cnt+1<=m) return true;
	return false; 
}
int main(int argc, char** argv) {
	scanf("%d%d",&n,&m);
	ll sum = 0,max = 0;
	for(int i = 0;i<n;i++){
		scanf("%d",&a[i]);
		if(a[i] > max) max = a[i];
		sum += a[i];
	}
	ll l = max,r = sum;
	while(l<r){
		ll mid = (l+r)/2;
		if(check(mid)) r = mid;
		else l = mid+1;
	}
	printf("%d",l);
	return 0;
}