程序设计方法学--2019/03/22--“Hankson的趣味题”_编程:hankson的趣味题-优快云博客

博客探讨了Hankson提出的正整数'逆问题'，即已知a0, a1, b0, b1，找到满足条件x与a0最大公约数为a1，与b0最小公倍数为b1的正整数x的数量。介绍了基础要求，如欧几里得算法和多值求解，以及提高要求，涉及数论和唯一分解定理，通过枚举b1的因子来求解问题。" 120822689,8393958,Ubuntu系统升级openSSH与openssl到8.8详细教程,"['Ubuntu', 'Linux', 'ssh', 'openssh', 'openssl']

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

程序设计方法学--2019/03/22--“Hankson的趣味题”

一、基本要求

求N个数的最大公约数和最小公倍数。用C或C++或java或python语言实现程序解决问题。

1. 程序风格良好(使用自定义注释模板)
2. 提供友好的输入输出，并进行输入数据的正确性验证。

二、提高要求

Hanks博士是BT（Bio-Tech，生物技术）领域的知名专家，他的儿子名叫Hankson。现在，刚刚放学回家的Hankson正在思考一个有趣的问题。
今天在课堂上，老师讲解了如何求两个正整数c₁和c₂的最大公约数和最小公倍数。现在Hankson认为自己已经熟练地掌握了这些知识，他开始思考一个“求公约数”和“求公倍数”之类问题的“逆问题”，这个问题是这样的：已知正整数a₀,a₁,b₀,b₁，设某未知正整数x满足：

x和a₀的最大公约数是a₁；
x和b₀的最小公倍数是b₁。

Hankson的“逆问题”就是求出满足条件的正整数x。但稍加思索之后，他发现这样的x并不唯一，甚至可能不存在。因此他转而开始考虑如何求解满足条件的x的个数。请你帮助他编程求解这个问题。

输入格式
输入第一行为一个正整数n，表示有n组输入数据。接下来的n行每行一组输入数据，为四个正整数a₀，a₁，b₀，b₁，每两个整数之间用一个空格隔开。输入数据保证a₀能被a₁整除，b₁能被b₀整除。

输出格式
输出共n行。每组输入数据的输出结果占一行，为一个整数。
对于每组数据：若不存在这样的x，请输出0；
若存在这样的x，请输出满足条件的x的个数；

样例输入	样例输出
2 41 1 96 288 95 1 37 1776	6 2

三、算法设计

1. 基础要求

欧几里得算法
$\, mod \, b)$
利用GCD求解LCM
$lcm(a,b)=\frac{a\cdot b}{gcd(a,b)}$
多值求解
$gcd(v_{1}, v_{2}, v_{3},..., v_{n})= \left\{ \begin{aligned} gcd(v_{n}, gcd(v_{n-1}, v_{n-2})) & , & n>2 \\ gcd(v_{1}, v_{2})\quad\quad\quad\quad\quad\,\,\, & , & n=2 \\ \end{aligned} \right.$

$lcm(v_{1}, v_{2}, v_{3},..., v_{n})=\frac{\prod ^n _{i=1}v_{i}}{gcd(v_{1}, v_{2}, v_{3},..., v_{n})^{n-1}}$

构建算法如下：

GCD
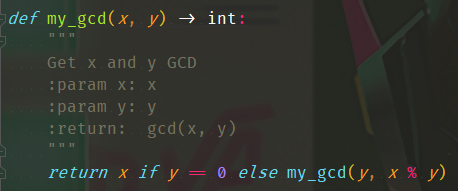
LCM（在my_lcm中调用my_gcd函数计算公约数)

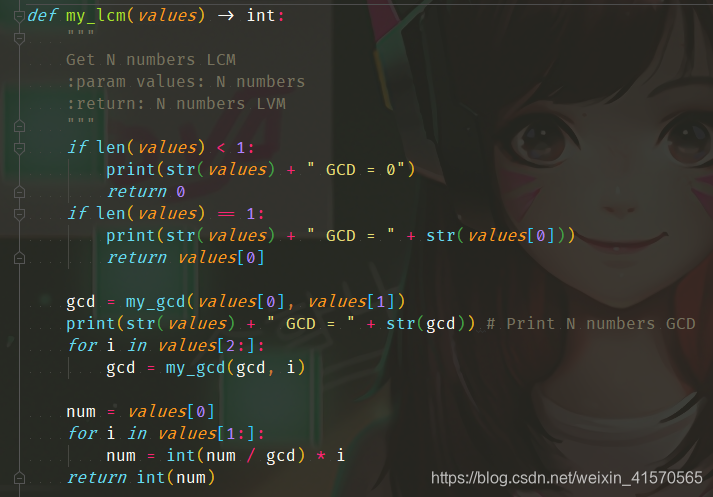
利用上述公式，进行循环迭代即可求解。
注意在计算LCM时，应当先除再乘避免数据溢出。

2. 提高要求

从题目中可以得知：
$\left\{ \begin{aligned} gcd(x,a_{0}) & = & a_{1} \\ \frac{x\cdot b_{0}}{gcd(x,b_{0})} & = & b_{1} \\ \end{aligned} \right.$
由数论唯一分解定理可以得出：
$\left\{ \begin{aligned} gcd\left( \frac{x}{a_{1}},\frac{a_{0}}{a_{1}} \right) & = & 1 \\ gcd\left( \frac{b_{1}}{b_{0}},\frac{b_{1}}{x} \right) & = & 1 \\ \end{aligned} \right.$
所以 x/a₁ 与 a₀/a₁ 互质，b₁/b₀ 与 b₁/x 互质。
又因为题中有a₁ > a₀ and b₁ > b₀，那么可以看出x是a₁的整数倍，同时x也是b₁的因子。
即：若b₁ mod a₁ ≠ 0，那么一定无解。
题意转换为枚举b₁的因子，那么： $\exist X|X=a_{1}\cdot K，K\in N^{+}$
写出算法：

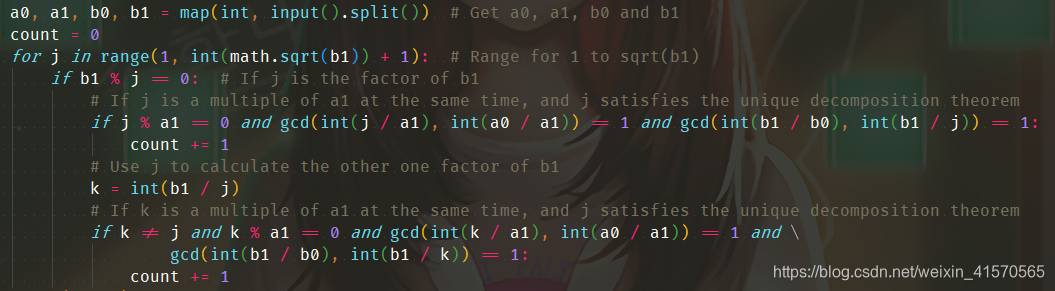
遍历到√(b₁ )即可，可减少迭代次数。

四、调试和测试

1. 调试（基本要求）

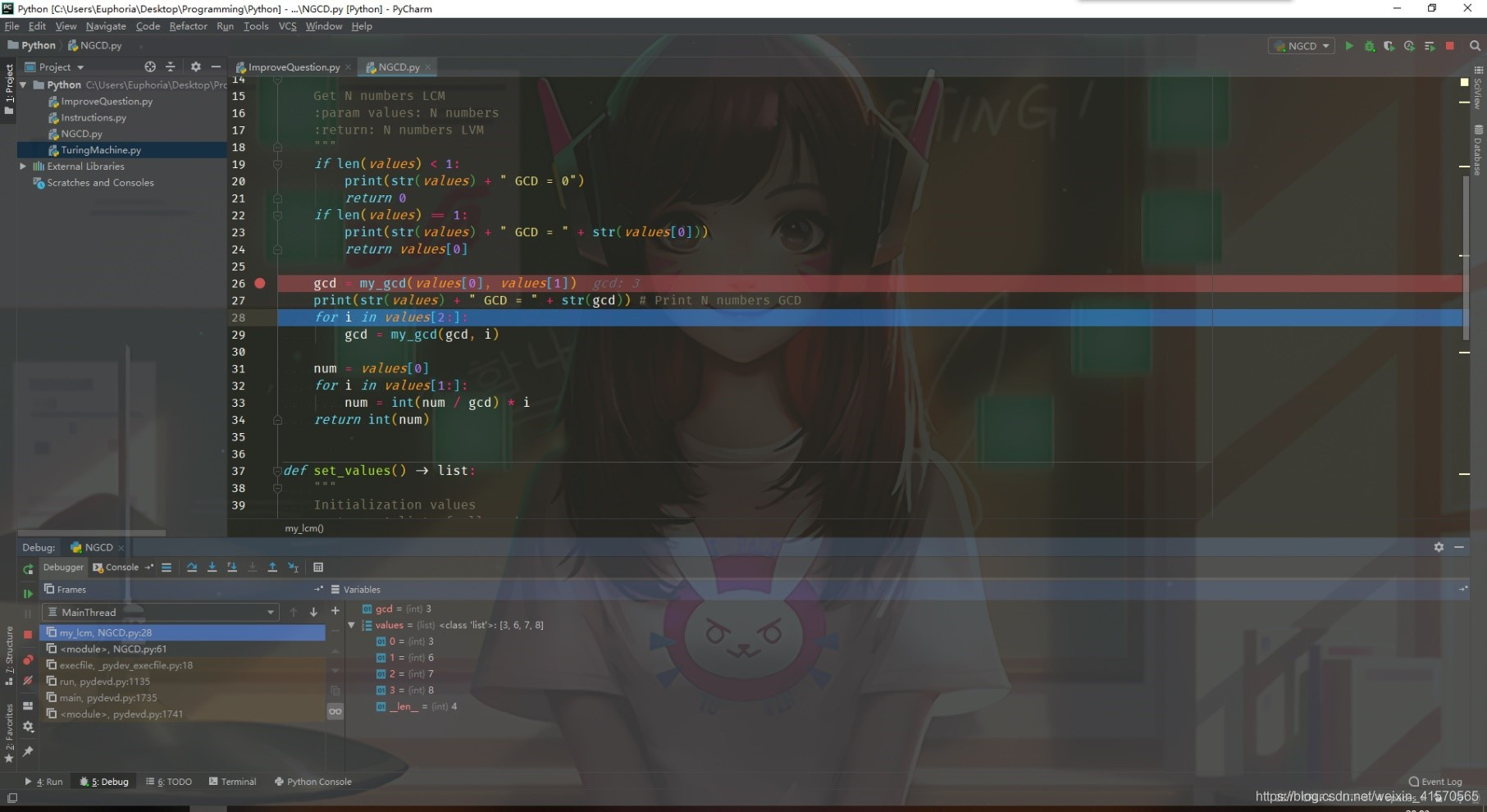
调试（基本要求）
输入3，6，7，8四个数，并进行计算（具有检测输入非法，即捕获Value Error异常，并且输入的数不小于1）

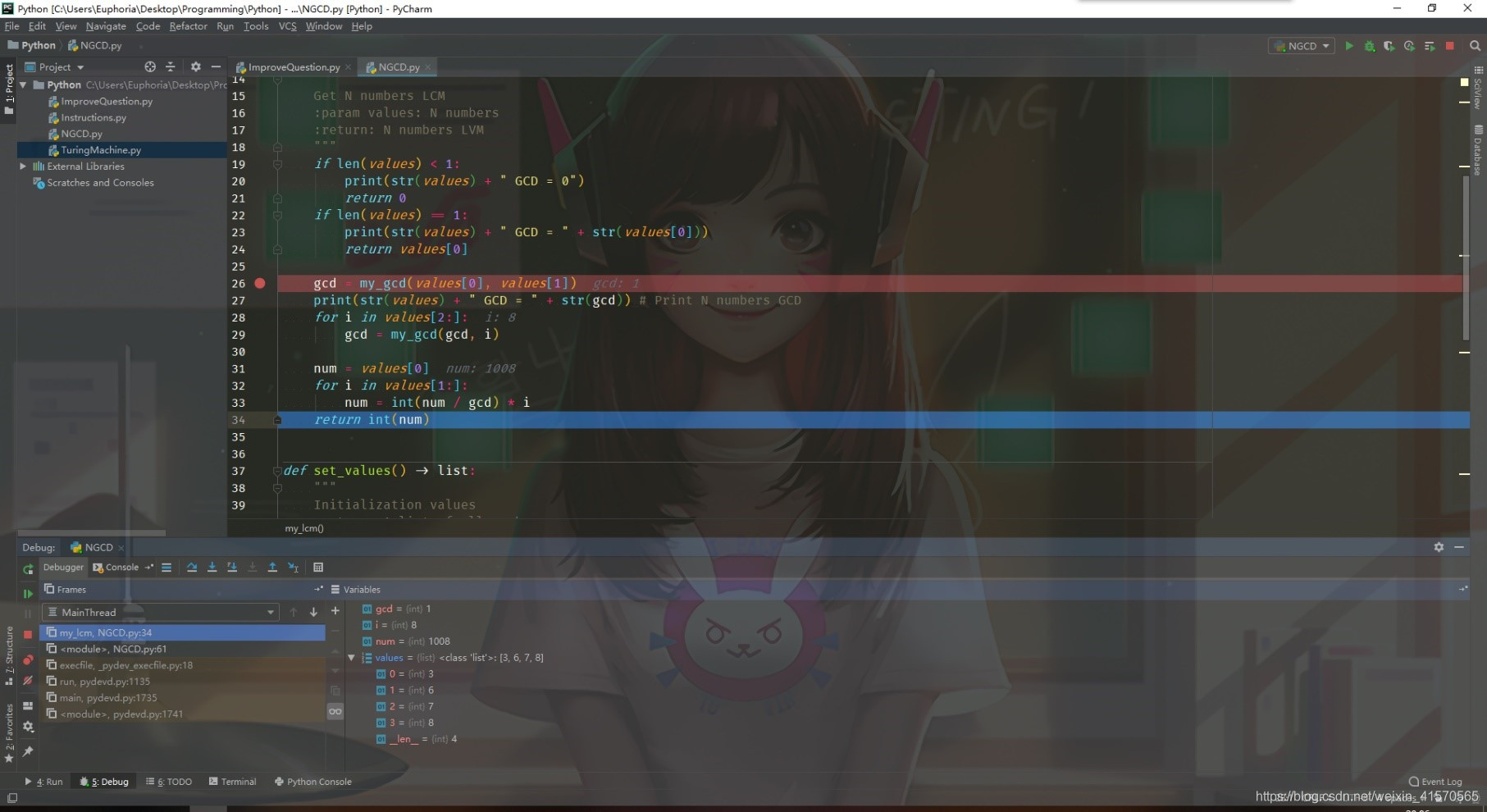
迭代计算最小公倍数。

2. 调试（提高要求）

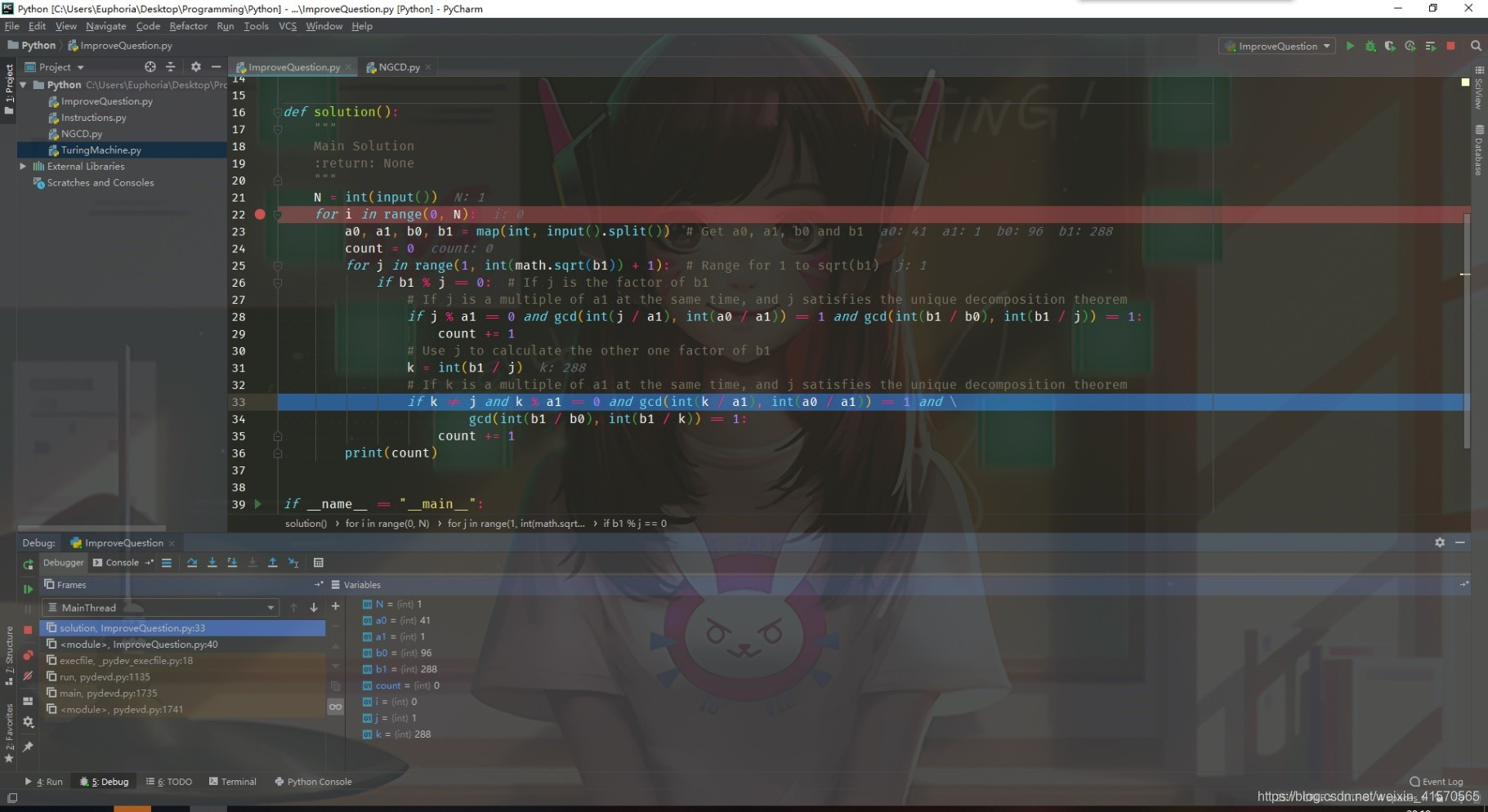
调试（提高要求）
输入测试用例后，迭代枚举b_1的因子，满足条件后更新计数器。

3. 测试（基础要求）

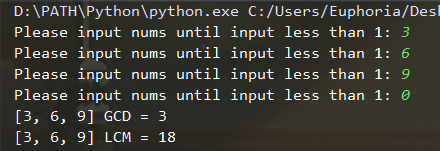
demo1
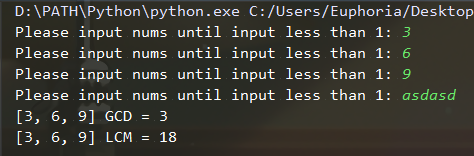
demo2

4. 测试（提高要求）

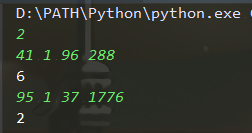
demo3

五、总结与归纳

基础部分对GCD和LCM的求解有了更深刻的认识，个人也推导出了下面的公式：
$gcd(v_{1}, v_{2}, v_{3},..., v_{n})= \left\{ \begin{aligned} gcd(v_{n}, gcd(v_{n-1}, v_{n-2})) & , & n>2 \\ gcd(v_{1}, v_{2})\quad\quad\quad\quad\quad\,\,\, & , & n=2 \\ \end{aligned} \right.$