KMP算法详解-优快云博客

本文深入讲解了KMP算法的工作原理及其实现过程，包括如何计算next数组和如何使用next数组来提高模式匹配效率，对比了朴素模式匹配算法的时间复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

部分转自 https://blog.youkuaiyun.com/starstar1992/article/details/54913261

定义

由零个或多个字符组成的有限序列，又叫字符串

空格串：是只包含空格的串。注意与空串不同（无长度）

子串与主串：串中任意个数的连续字符组成的子序列，包含子串的串称为主串

子串在主串中的位置：是子串的第一个字符在主串中的序号

串的模式匹配

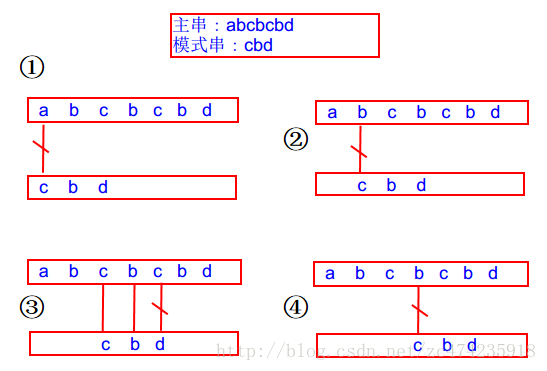
子串的定位操作例如从文档中找到所有 “hello”

朴素的模式匹配算法

朴素的模式匹配算法，就是把要查找的内容，一步步的与要查找的文章进行进行比较。如果匹配失败，则主串和字串回溯。子串位置加1.重新匹配。

模式匹配算法的流程如下：

/*不用串的其他操作，只用基本的数组实现*/
/*返回子串T在主串S中第pos个字符之后的位置。若不存在，则函数返回值为0*/
/*T非空，1<=pos<=strlength(s)*/
int  index(String S, String T, int pos)
{
	int i = pos;//i用于主串S中当前位置下标。若pos不为1，则从pos位置开始匹配
	int j = 1;//j用于子串T中当前位置下标值
	while（i <= S.size() && j <= T.size())//当i小于S的长度且j小于T的长度时循环
	{
	if (S[i] == T[j])
	{
		++i;
		++j;
	}
	else  //指针后退，重新开始匹配
	{
		i = i - j + 2;//i退回到上次匹配首位的下一位
		j = 1;
	}
}
	if (j > T.size())
		return i - T.size();
	else return 0;
}

时间复杂度O(（n-m+1）*m)

KMP模式匹配算法

KMP算法求解什么类型问题

字符串匹配。给你两个字符串，寻找其中一个字符串是否包含另一个字符串，如果包含，返回包含的起始位置。
如下面两个字符串：

char *str = "bacbababadababacambabacaddababacasdsd";
char *ptr = "ababaca";

str有两处包含ptr
分别在str的下标10，26处包含ptr。

“bacbababadababacambabacaddababacasdsd”;\
这里写图片描述

问题类型很简单，下面直接介绍算法

算法说明

一般匹配字符串时，我们从目标字符串str（假设长度为n）的第一个下标选取和ptr长度（长度为m）一样的子字符串进行比较，如果一样，就返回开始处的下标值，不一样，选取str下一个下标，同样选取长度为n的字符串进行比较，直到str的末尾（实际比较时，下标移动到n-m）。这样的时间复杂度是O(n*m)。

KMP算法：可以实现复杂度为O(m+n)

在朴素的匹配算法中，无论已经匹配正确了多少个字符，在遇到不配的情况下，指针就要进行回溯。重新开始下一轮匹配。这样就会造成资源的浪费。

KMP算法，不回溯，消除了这种浪费。

考察目标字符串ptr：
ababaca
这里我们要计算一个长度为m的转移函数next。

next数组的含义就是一个固定字符串的最长前缀和最长后缀相同的长度。

比如：abcjkdabc，那么这个数组的最长前缀和最长后缀相同必然是abc。
cbcbc，最长前缀和最长后缀相同是cbc。
abcbc，最长前缀和最长后缀相同是不存在的。

**注意最长前缀：是说以第一个字符开始，但是不包含最后一个字符。
比如aaaa相同的最长前缀和最长后缀是aaa。**
对于目标字符串ptr，ababaca，长度是7，所以next[0]，next[1]，next[2]，next[3]，next[4]，next[5]，next[6]分别计算的是
a，ab，aba，abab，ababa，ababac，ababaca的相同的最长前缀和最长后缀的长度。由于a，ab，aba，abab，ababa，ababac，ababaca的相同的最长前缀和最长后缀是“”，“”，“a”，“ab”，“aba”，“”，“a”,所以next数组的值是[-1,-1,0,1,2,-1,0]，这里-1表示不存在，0表示存在长度为1，2表示存在长度为3。这是为了和代码相对应。

下图中的1，2，3，4是一样的。1-2之间的和3-4之间的也是一样的，我们发现A和B不一样；之前的算法是我把下面的字符串往前移动一个距离，重新从头开始比较，那必然存在很多重复的比较。现在的做法是，我把下面的字符串往前移动，使3和2对其，直接比较C和A是否一样。

这里写图片描述

模式匹配字符串中存在重复元素情况下：

/*目标子串的next数组*/
void cal_next(char *str, int *next, int len)
{
    next[0] = -1;//next[0]初始化为-1，-1表示不存在相同的最大前缀和最大后缀
    int k = -1;//k初始化为-1
    for (int q = 1; q <= len-1; q++)
    {
        while (k > -1 && str[k + 1] != str[q])//如果下一个不同，那么k就变成next[k]，注意next[k]是小于k的，无论k取任何值。
        {
            k = next[k];//往前回溯,看是否有与str[q]相同的字母
        }
        if (str[k + 1] == str[q])//如果相同，k++
        {
            k = k + 1;
        }
        next[q] = k;//这个是把算的k的值（就是相同的最大前缀和最大后缀长）赋给next[q]
    }
}

举例：

a b a b c

q 0 1 2 3 4

1、首先next[0]=-1，进入for循环，q=1,while不能执行，if不能执行，next[1]=-1，q=2

2、再次进入for循环,while不能执行，if可以执行，k=0,next[2]=0,q=3

3、再次进入for循环，while不可以执行因为str[0+1]==str[3],if执行，k=1, next[3]=1，q=4

4、再次进入for循环，while 可以执行因为str[1+1]!=str[4], k=next[1]=-1,退出while循环，但if不执行，next[4]=-1

5、结束

KMP算法

int KMP(char *str, int slen, char *ptr, int plen)
{
    int *next = new int[plen];
    cal_next(ptr, next, plen);//计算next数组
    int k = -1;
    for (int i = 0; i < slen; i++)
    {
        while (k >-1&& ptr[k + 1] != str[i])//ptr和str不匹配，且k>-1（表示ptr和str有部分匹配）
            k = next[k];//往前回溯
        if (ptr[k + 1] == str[i])
            k = k + 1;
        if (k == plen-1)//说明k移动到ptr的最末端
        {
            //cout << "在位置" << i-plen+1<< endl;
            //k = -1;//重新初始化，寻找下一个
            //i = i - plen + 1;//i定位到该位置，外层for循环i++可以继续找下一个（这里默认存在两个匹配字符串可以部分重叠），感谢评论中同学指出错误。
            return i-plen+1;//返回相应的位置
        }
    }
    return -1;  
}

举例

i 主串str： a b a b a b d

i、k : 0 1 2 3 4 5 6

k 子串ptr： a b a b d next[5]={-1,-1,0,1,-1}

1、k=-1,while不执行，因为k=-1,if执行，k=0,i=1

2、for循环执行，while不执行，因为str[1]==ptr[1],if执行，k=1,i=2

3、for循环执行，while不执行，因为str[2]==ptr[2],if执行，k=2,i=3

4、for循环执行，while不执行，因为str[3]==ptr[3],if执行，k=3,i=4

5、for循环执行，while执行，因为str[4]!=ptr[4],k=next[3]=1

因为到i=4时出现不相等，那我们只有向前找， k=next[k]这操作就是看子串是否有重复

如果有重复，那么我们就不必找到ptr的最前面，因为next[k]是最长前缀的长度，而因为其重复，所以str中0~next[k]的长度都是与str匹[i]之前的字符匹配的（因为前面已经比较过），因此只需比较next[k]+1与str[i]及其以后的字符。

如果无重复，肯定要从ptr开始位置比较，而此时不重复的next[k]等于-1，回到开始位置

6、for循环 ,while不执行，if执行，k=3,i=6

7、for 循环，while不执行，if执行，k=4,return i-k+1=3

利用k=next[k]的目的就是当主串中前一部分与子串相同，但后一部分不相同时，用于

测试

    char *str = "bacbababadababacambabacaddababacasdsd";
    char *ptr = "ababaca";
    int a = KMP(str, 36, ptr, 7);
    return 0;

注意如果str里有多个匹配ptr的字符串，要想求出所有的满足要求的下标位置，在KMP算法需要稍微修改一下。见上面注释掉的代码。

时间复杂度分析O（n+m）