推荐系统 - 召回 - 基于矩阵分解的算法

对于一个评分矩阵User-Item Matrix，第i行第j列表示第i个用户对于第j个物品的喜爱程度（这个喜爱程度可以通过用户的行为，包括搜索、浏览、加购物车、购买等来表征）。这个矩阵是很稀疏的，因为用户对于商品的行为是很不充分的，一个用户对大部分商品的行为根本没有记录。我们的任务是要通过分析已有的数据（观测数据）来对未知数据进行预测（预测某个用户u对于他根本没见过的商品i会有多少的喜爱程度），即这是一个矩阵补全（填充）任务。矩阵填充任务可以通过矩阵分解技术来实现。核心思想是将用户和商品映射到一个共同的k维隐空间，使得在这个隐空间中，用户对商品的喜爱程度可以使用向量内积来计算。这一隐空间借助从评分矩阵自动推断得到的隐因子，来刻画用户和商品，以解释用户对商品的评分行为。

1. Traditional SVD

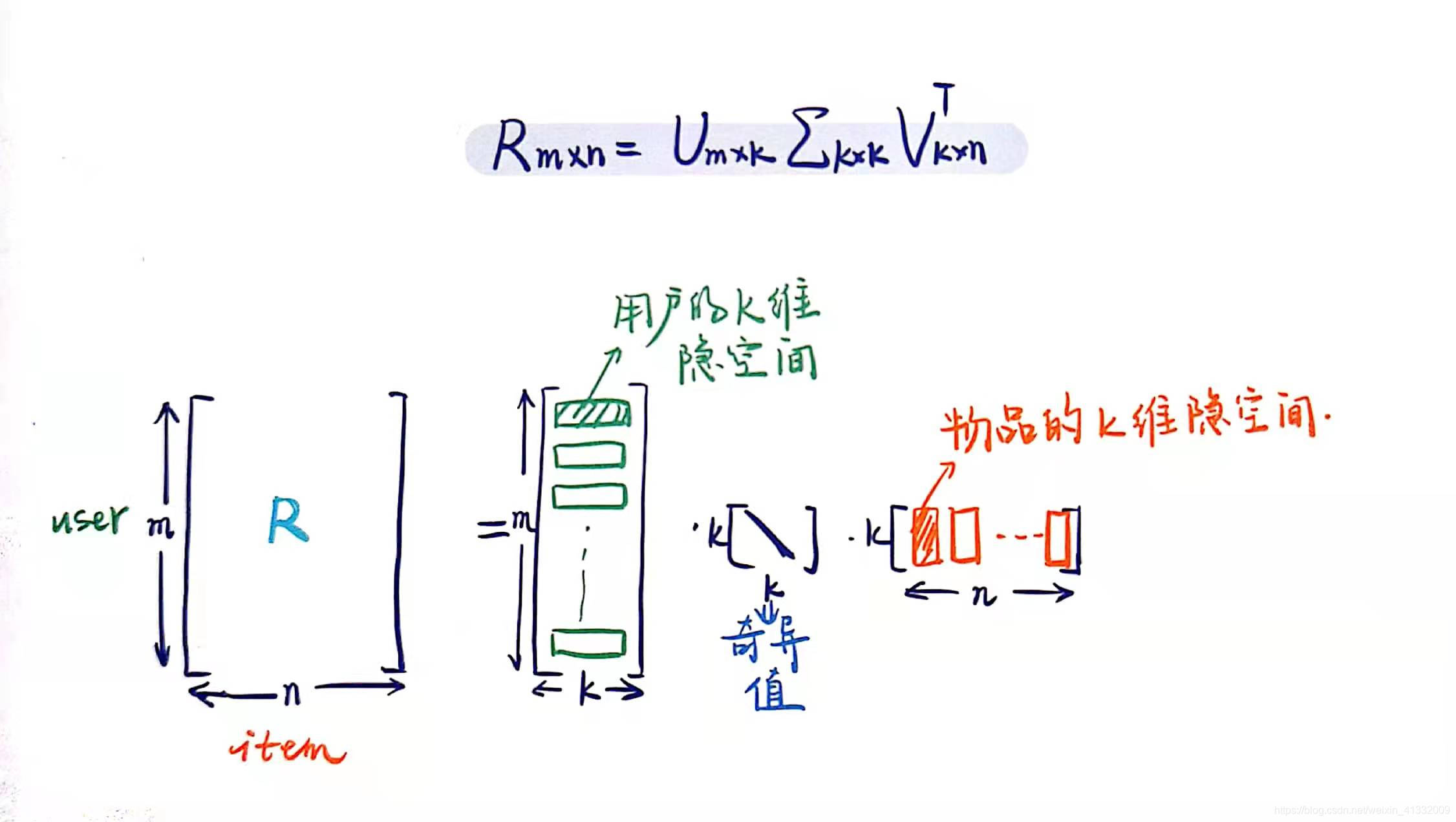
R矩阵是用户对商品的喜爱程度矩阵。

SVD分解的形式为3个矩阵相乘，中间矩阵为奇异值矩阵。如果想运用SVD分解的话，有一个前提是要求矩阵是稠密的，即矩阵里的元素要非空，否则就不能运用SVD分解。

很显然我们的任务还不能用SVD，所以一般的做法是先用均值或者其他统计学方法来填充矩阵，然后再运用SVD分解降维。

2. FunkSVD / ALS（Alternating Least Squares）

2.1 矩阵分解

ALS算法是2008年以来，用的比较多的协同过滤算法。它已经集成到Spark的Mllib库中。

从协同过滤的分类来说，ALS算法属于 User-Item CF，也叫做混合CF，它同时考虑了User和Item两个方面。用户和商品的关系，可以抽象为如下的三元组：<User,Item,Rating>。其中，Rating是用户对商品的评分，表征用户对该商品的喜好程度。

假设我们有一批用户数据，其中包含m个User和n个Item，则我们定义矩阵R，其中第u行第i列表示第u个User对第i个Item的评分。

• 在实际使用中，由于n和m的数量都十分巨大，因此R矩阵的规模很容易就会突破1亿项。这时候，传统的矩阵分解方法对于这么大的数据量已经是很难处理了。
• 另一方面，一个用户也不可能给所有商品评分，因此，R矩阵注定是个稀疏矩阵。矩阵中所缺失的评分，又叫做missing item。

刚才提到的Traditional SVD首先需要填充矩阵，然后再进行分解降维，同时存在计算复杂度高和空间消耗大的问题。FunkSVD/ALS不再将矩阵分解为3个矩阵，而是分解为2个低秩的用户和商品矩阵。

一般情况下，k的值远小于n和m的值，从而达到了数据降维的目的。这里的表明这个投射只是一个近似的空间变换。一般情况下，k的值远小于n和m的值，从而达到了数据降维的目的。

幸运的是，我们并不需要显式的定义这些关联维度，而只需要假定它们存在即可，因此这里的关联维度又被称为Latent factor。k的典型取值一般是20～200。

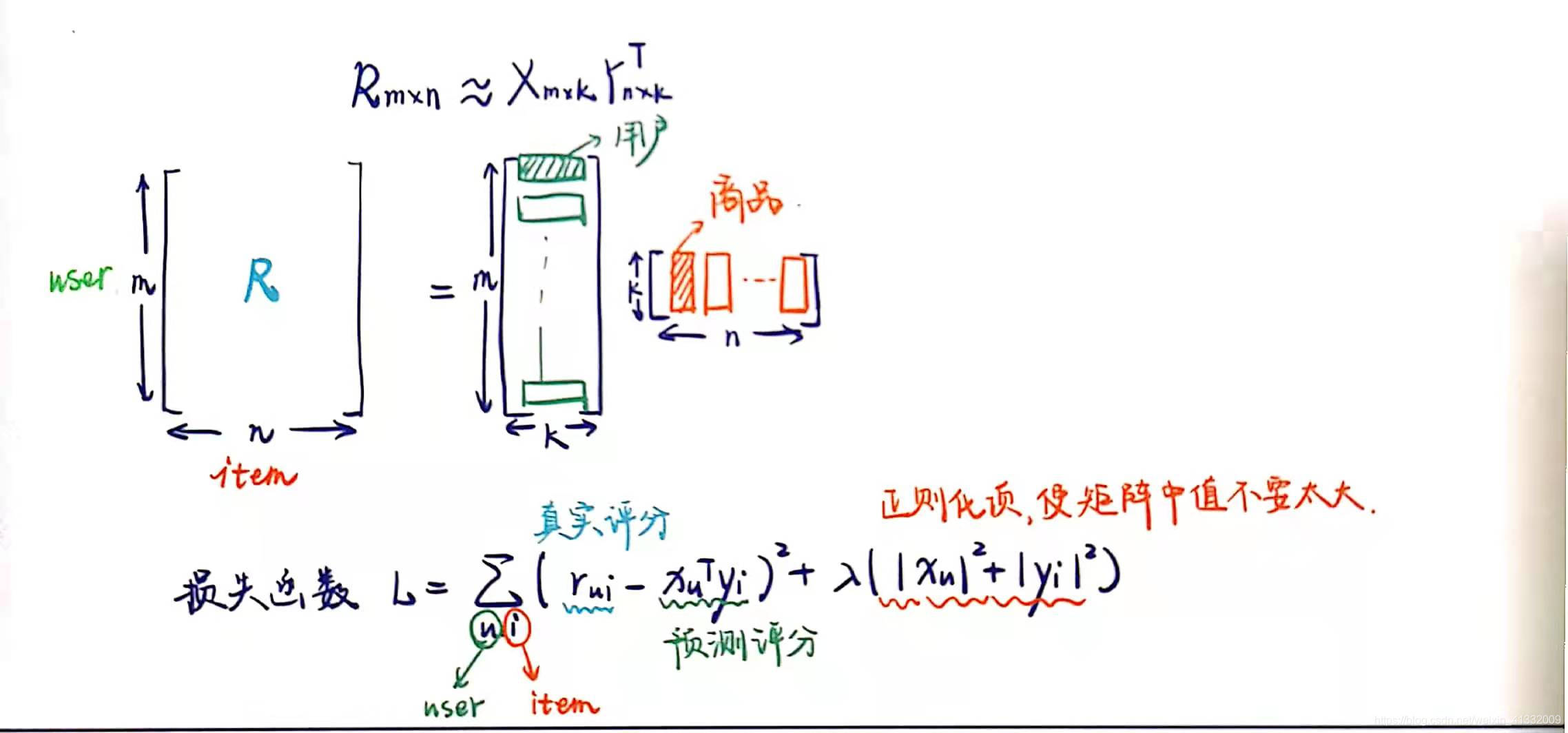
为了使低秩矩阵X和Y尽可能地逼近R，需要最小化下面的平方误差损失函数：

这里，指的是第u个用户的k维隐向量表示(图中横着的红色向量)，指的是第i个商品的隐向量表示(图中竖着的红色向量)。将它们做内积，可以得到计算的评分. loss就是RMSE
考虑到矩阵的稳定性问题，使用 L2 正则化项，则上式变为：

优化上式，得到训练结果矩阵。预测时，将User和Item代入，即可得到相应的评分预测值。
同时，矩阵X和Y，还可以用于比较不同的User（或Item）之间的相似度，如下图所示

ALS算法的缺点在于：

1.它是一个离线算法。

2.无法准确评估新加入的用户或商品。这个问题也被称为Cold Start问题。

2.2 ALS算法优化过程的推导

将损失函数L对用户隐向量求导，得到：

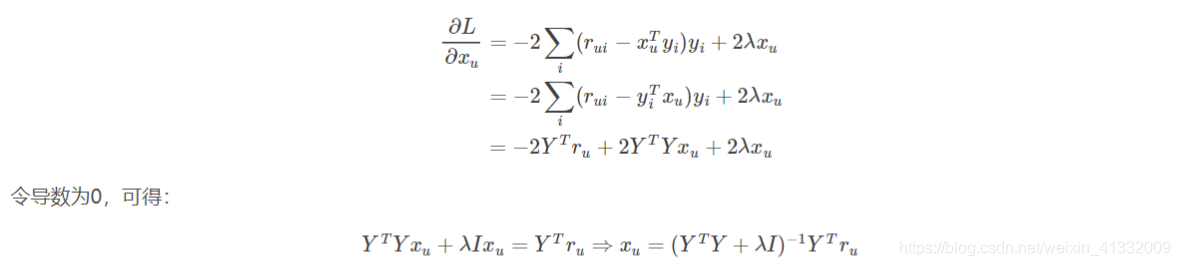
同理，将损失函数L对物品隐向量求导，得到：

因此整个优化迭代的过程为：

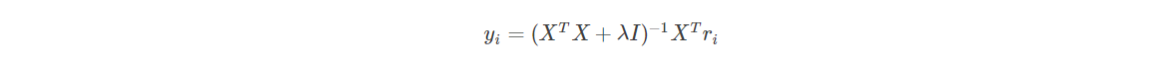
1. 随机生成用户隐矩阵X和商品隐矩阵Y

2. repeat until convergence{

    2.1 固定Y，用更新X

    2.2 固定X，用更新Y

}

因为这个过程交替优化X、Y，因此被称为交替最小二乘法(Alternating Least Squares)