【Udacity】3,5,12，相关性

最新推荐文章于 2022-04-21 11:41:07 发布

原创最新推荐文章于 2022-04-21 11:41:07 发布 · 305 阅读

0 ·

CC 4.0 BY-SA版权

R 专栏收录该内容

40 篇文章

订阅专栏

本文介绍如何使用Pearson相关系数评估变量间的线性关系，并通过子集相关性分析深入理解数据特性。此外，还探讨了如何利用散点图直观展现变量间的关系，并提供了处理异常值的方法。最后，文章讨论了相关性在实际研究中的复杂性和潜在误导。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1、相关性
相关性图解指南：
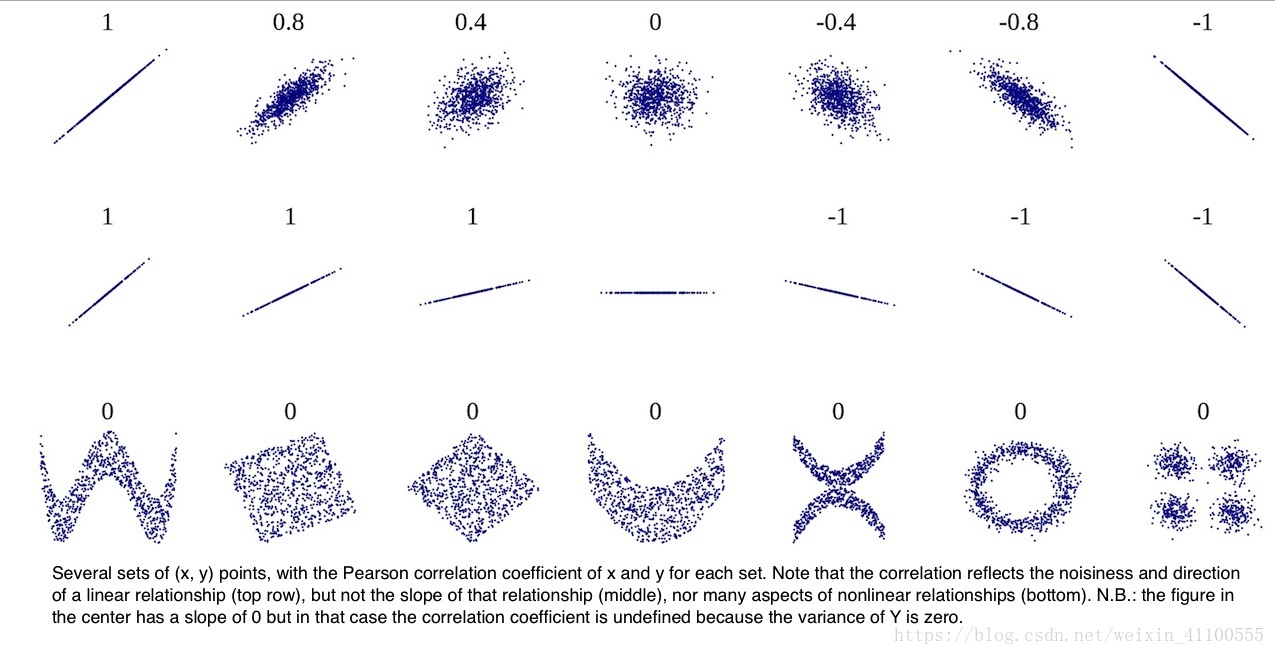
这里写图片描述
相关系数
 推论统计学入门-相关系数
相关系数除了用字母 r 表示以外，通常还用希腊字母 ρ 表示。
计算相关系数的默认方法是 Pearson，大多数统计软件都是如此。你无需在计算 Pearson 积差相关时传递方法参数。

> cor.test(pf$age,pf$friend_count,method = "pearson")

    Pearson's product-moment correlation

data:  pf$age and pf$friend_count
t = -8.6268, df = 99001, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.03363072 -0.02118189
sample estimates:
        cor 
-0.02740737

关联大于0.3或者小于-0.3 表示有意义但是关联较小
0.5左右为中等
0.7以上为很大

> with(pf,cor.test(age,friend_count,method = "pearson"))

    Pearson's product-moment correlation

data:  age and friend_count
t = -8.6268, df = 99001, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.03363072 -0.02118189
sample estimates:
        cor 
-0.02740737

2、子集相关性

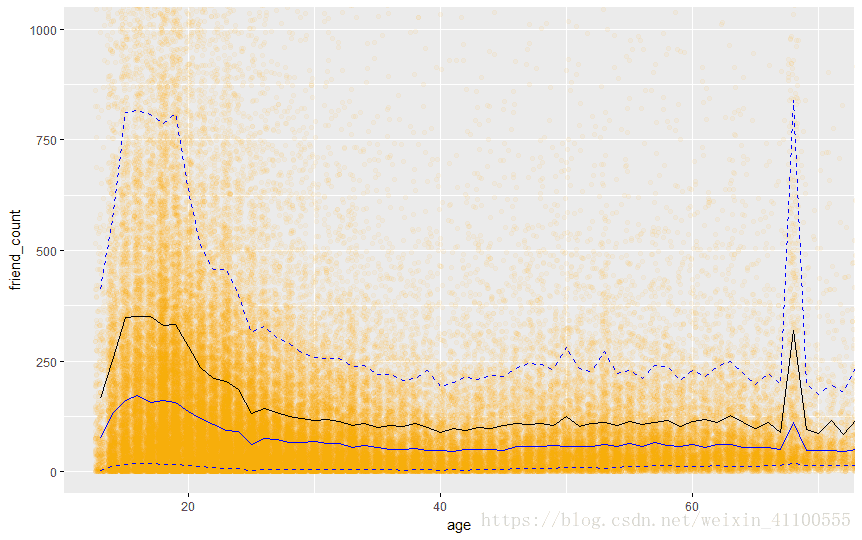
这里写图片描述
我们通过观察图片，我们发现不同的区间相关性不同，我们希望分不同区域来计算相关性。

> with(**subset(pf,pf$age<=70)**,cor.test(age, friend_count))

    Pearson's product-moment correlation

data:  age and friend_count
t = -52.592, df = 91029, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1780220 -0.1654129
sample estimates:
       cor 
-0.1717245

3、相关分析法
相关分析法
4、创建散点图
相关系数有用，但是它并不能代替从散点图以及其他图形中观察到的内容

ggplot(aes(x=likes_received,y=www_likes_received),data=pf)+
  geom_point()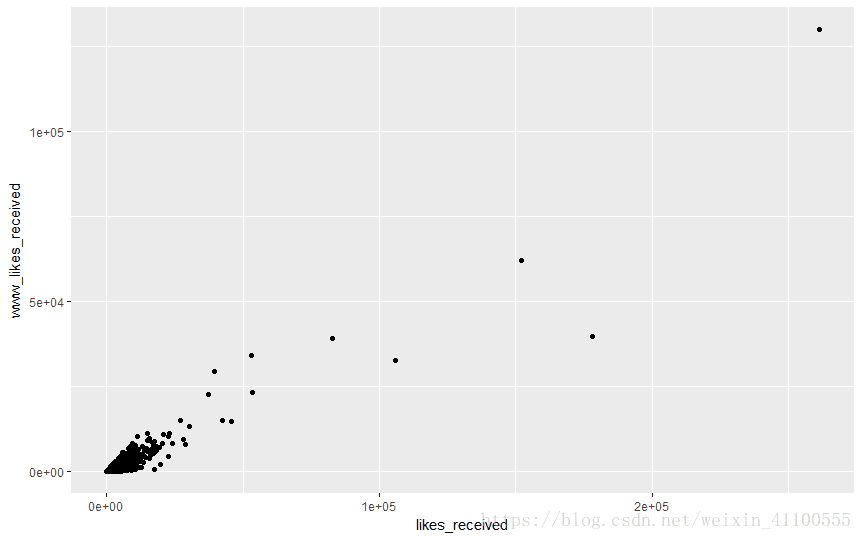

这里写图片描述
4、强相关
相关系数在 X 或 Y 的线性转换下是不变的，并且当 X 和 Y 都被转换为 z 分数时，回归线的斜率就是相关系数。
值得注意的是，我们并不总是对大部分数据感兴趣。有时候，我们关注的是异常值，而且重要的是，我们要了解它们的值以及它们为何出现在数据集中。
看上面的图，有一些跳跃的异常值。我们可以使用Quantile函数来设置x和y轴的极限。

ggplot(aes(x=likes_received,y=www_likes_received),data=pf)+
  geom_point()+
  xlim=(0,quantile(pf$likes_received,0.95))+
  ylim=(0,quantile(pf$www_likes_received,0.95))+
  geom_smooth(method = 'lm',color='red')

以上代码执行有问题，原因是xlim和ylim后面不能跟=，直接删除等号即可

ggplot(aes(x=likes_received,y=www_likes_received),data=pf)+
  geom_point()+
  xlim(0,quantile(pf$likes_received,0.95))+
  ylim(0,quantile(pf$www_likes_received,0.95))+
  geom_smooth(method = 'lm',color='red')

5.moria对于相关的研究
强相关并不一定都是好事
1、绘制三点图来观察相关量，同时计算相关系数来真是的量化相关性。
2、做递归，对数据进行建模，将某些变量放入递归。递归的一个假设就是这些变量彼此独立，如果任何两个变量彼此高度相关，实际上难以判断哪个变量产生的这种现象。
3、重要的一点是，首先衡量变量之间的相关性。通常可以帮助你确认哪些变量不要一起投入。可以帮助你判断，实际上报保留哪些变量。
4、相关性可能也存在欺骗性。