概率图模型

概率图模型：用观测结点表示观测到的数据，用隐含结点表示潜在的知识， 用边来描述知识与数据的相互关系，最后基于这样的关系图获得一个概率分布 。节点对应于随机变量，边对应于随机变量的依赖或相关关系，有向边表示单向的依赖，无向边表示无依赖关系 。
概率图模型分为贝叶斯网络和马尔可夫网络两大类 。 贝叶斯网络可以用一个有向图结构表示，马尔可夫网络可以表示威一个无向图的网络结构 。

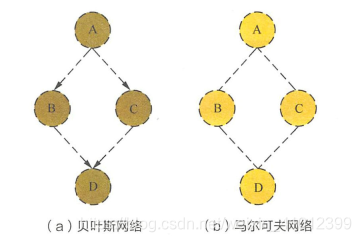
朴素贝叶斯原理：

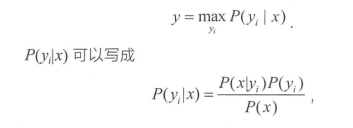
马尔科夫原理：
假设一个随机过程中， t 时刻的状态 x 的条件分布，仅仅与当前一个状态有关，则称为马尔可夫过程，时间和状态的取值都是离散的马尔可夫过程也称为马尔可夫链 。

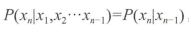
隐马尔可夫模型是对含有未知参数（隐状态）的马尔可夫链进行建模的生成模型，隐马尔可夫模型包括概率计算问题、预测问题、学习问题三个基本问题 。
( 1 ）概率计算问题。己知模型的所有参数，计算观测序列 Y 出现的概率，可使用前向和后向算法求解。
( 2 ）预测问题。 已知模型所有参数和观测序列 Y，计算最可能的隐状态序列 X，可使用经典的动态规划算法一一维特比算法来求解最可能的状态序列。
( 3 ）学习问题 ： 己知观测序列 Y，求解使得该观测序列概率最大的模型参数，包捂隐状态序列、隐状态之间的转移概率分布以及从隐状态到观测状态的概率分布，可使用 Baum -Welch 算法进行参数的学习， Baum-Welch 算法是最大期望算法的一个特例 。